O que é Volatilidade? Como podemos calcular essa métrica? Este artigo apresenta uma breve introdução à volatilidade, descreve como podemos calcular a volatilidade utilizando Modelos de Volatilidade Condicional e demonstra a aplicação prática dessa abordagem para estimar a volatilidade da taxa de câmbio BRL/USD por meio da linguagem de programação Python.
Estimando a Volatilidade do Câmbio no Python
Uma importante medida em finanças é o risco associado a um ativo e a volatilidade de ativos é talvez a medida de risco mais utilizada. Ainda que a volatilidade seja bem definida, ela não é diretamente observada na prática. Nós observamos os preços dos ativos e seus derivativos. A volatilidade deve ser, então, estimada com base nesses preços observados. Ainda que a volatilidade não seja diretamente observada, ela apresenta algumas características comuns associadas aos retornos dos ativos. Listamos abaixo algumas delas:
- A volatilidade é alta em certos períodos e baixa em outros, configurando o que a literatura chama de volatility clusters;
- A volatilidade evolui de maneira contínua, de modo que saltos não são comuns;
- A volatilidade costuma variar em um intervalo fixo;
- A volatilidade costuma reagir de forma diferente a um aumento muito grande nos preços e a um decréscimo igualmente muito grande, com o último representando maior impacto.
Essas características implicam que, de modo geral, a volatilidade é uma série estacionária. Ademais, essas características determinam a forma como os modelos serão construídos.
De fato, alguns modelos de volatilidade são formatados justamente para corrigir a inabilidade dos atualmente existentes em capturar algumas das características mencionadas acima.
Na prática, estima-se a volatilidade de um ativo com base nos seus preços ou derivativos. Tipicamente, três tipos de volatilidade são consideradas:
- Volatilidade como o desvio padrão condicional dos retornos diários;
- Volatilidade implícita, obtida a partir de fórmulas de precificação (como Black-Scholes), com base nos preços do mercado de opções, é possível deduzir a volatilidade do preço da ação. Um exemplo desse tipo de procedimento é o VIX Index;
- Volatilidade realizada, obtida com base em dados financeiros de alta frequência, como, por exemplo, retornos intraday de 5 minutos.
Modelagem
Com efeito, para estimar a volatilidade da taxa de câmbio BRL/USD, primeiro, precisamos pegar a série via Sistema de Séries Temporais do Banco Central.
Feito isso, podemos calcular o log retorno da série, estimar um modelo GARCH(1,1) para os mesmos, extraindo assim a série de volatilidade.
Para a volatilidade do Câmbio, usamos um modelo GARCH(1,1).
Definição do Modelo
Um modelo GARCH(1,1) (Generalized Autoregressive Conditional Heteroskedasticity) é uma forma de modelar a volatilidade condicional em séries temporais financeiras. Para entendermos o modelo, devemos compreender o modelo ARCH e os seus termos.
Os modelos ARCH (Autoregressive Conditional Heteroskedasticity) são usados para modelar a heterocedasticidade condicional em séries temporais financeiras, ou seja, a variabilidade condicional da volatilidade ao longo do tempo. Os termos principais em um modelo ARCH incluem:
1. Erro Condicional : O erro condicional representa a diferença entre o valor observado da série temporal no período
e o valor previsto pelo modelo. Em um modelo ARCH, a variância desse erro não é constante ao longo do tempo, e é isso que o modelo tenta capturar.
2. Variância Condicional : A variância condicional é a variabilidade da série temporal em um determinado período de tempo, condicionada às informações anteriores. Ela não é constante, como é o caso de séries temporais com heterocedasticidade condicional. A variância condicional no período
é denotada por
.
As suposições e restrições típicas associadas a um modelo GARCH(1,1) incluem:
1. Séries Temporais Estacionárias: O modelo assume que a série temporal é estacionária, o que significa que a média e a variância condicionais são constantes ao longo do tempo. Se a série não for estacionária, pode ser necessário aplicar diferenciação ou transformações para torná-la estacionária.
2. Erros Condicionais Independentes e Identicamente Distribuídos: Os erros são assumidos como ruído branco, o que significa que são independentes entre si e têm a mesma distribuição, com média zero e variância constante.
3. Condições de Positividade: Os parâmetros ,
, e
devem satisfazer condições de positividade para garantir que a volatilidade condicional seja não negativa.
4. Condição de Estacionariedade: Para que o modelo seja estável, é necessário que . Isso garante que a série temporal seja estacionária no sentido fraco.
Para a montagem do Modelo, seguimos o seguinte processo:
1. Especificar uma equação de média, testando a dependência serial nos dados e, se necessário, construindo um modelo econométrico (por exemplo, um modelo ARMA) para a série de retornos, a fim de eliminar qualquer dependência linear.
2. Utilizar os resíduos da equação de média para testar os efeitos ARCH e verificar a distribuição de dados que melhor representa o modelo.
3. Especificar um modelo de volatilidade se os efeitos ARCH forem estatisticamente significativos e realizar uma estimação conjunta das equações de média e volatilidade.
4. Verificar o modelo ajustado cuidadosamente e refiná-lo, se necessário.
Vamos aplicar o GARCH(1,1) para série de primeira diferença logaritimizada do Câmbio R.
Dados do Câmbio
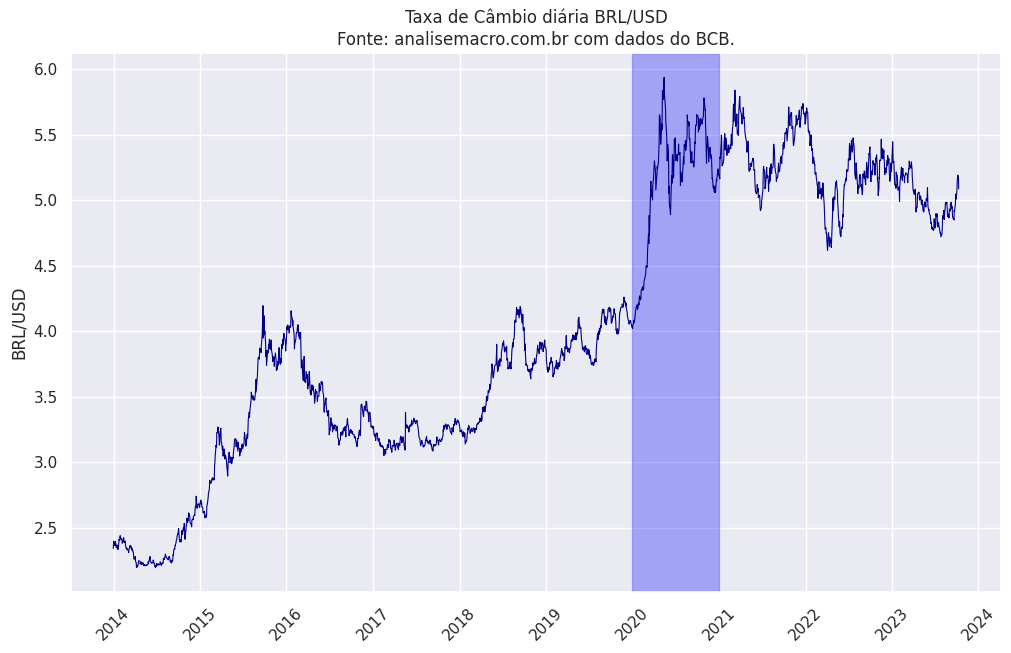
Primeiramente, é essencial realizar uma análise dos dados de câmbio. Por meio do gráfico abaixo, podemos observar as variações nos preços dessa variável, destacando a significativa elevação ocorrida em 2020.
A série no nível apresenta características de um passeio aleatório. Portanto, é necessário realizar uma transformação na série. Optamos por calcular o retorno logaritmo, cujo resultado é apresentado abaixo. Conforme mencionado, é possível notar a presença de clusters de volatilidade na série, sugerindo a existência de heterocedasticidade e variação condicional.
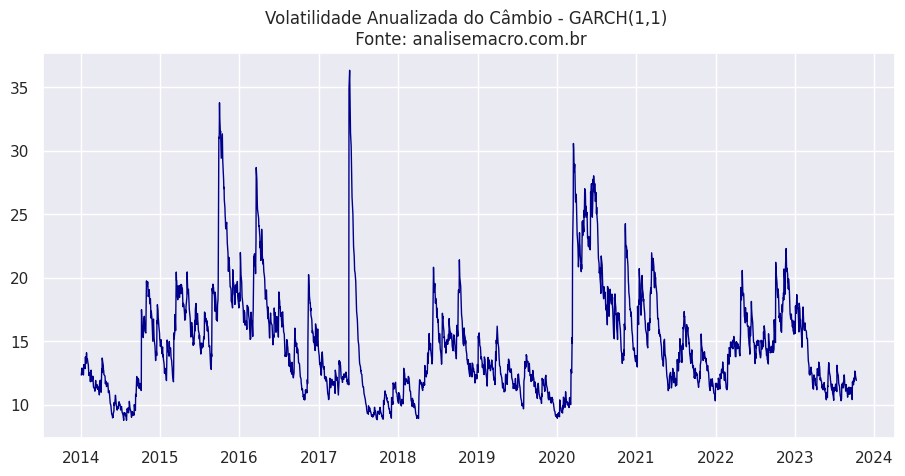
Com base nessa análise, procedemos à estimação da série utilizando um modelo GARCH(1,1). O gráfico a seguir exibe o resultado da variância condicional calculada, expressa em termos anualizados.
Quer aprender mais?
Clique aqui para fazer seu cadastro no Boletim AM e baixar o código que produziu este exercício, além de receber novos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas diretamente em seu e-mail.
Referências
R. L. S. Bueno. Econometria de Séries Temporais. Editora Cengage Learning, 2011.
R. S. Tsay. An Introduction to Analysis of Financial Data with R. Editora Wiley, 2013.