A despeito de sua simplicidade operacional, modelos univariados ainda são bastante utilizadas para fins de modelagem e previsão de um amplo conjunto de variáveis econômicas. Nesse post, vamos ilustrar a aplicação desses modelos sobre a inflação brasileira medida pelo IPCA. Em particular, estamos interessados em modelos do tipo ARIMA. Esses modelos podem ser representados em termos de notação polinomial como
(1)
Para o caso específico da inflação, como veremos na sequência, a equação 1 precisa ser reformulada. Isto porque, os modelos ARIMA também são capazes de modelar uma ampla gama de dados sazonais, como é o caso da inflação brasileira. Um modelo ARIMA sazonal é formado pela inclusão de termos sazonais adicionais, na forma , onde o segundo componente faz referência à parte sazonal e
significa o número de períodos por estação. Em termos formais,
(2)
Na sequência desse post, vamos aplicar a equação 2 à inflação brasileira. Para começar, precisamos carregar alguns pacotes de R como abaixo.
library(forecast) library(tidyverse) library(gridExtra) library(xtable) library(rbcb) library(scales) library(tsutils) library(tsibble) library(feasts)
Carregados os pacotes que utilizaremos, podemos pegar os dados da inflação medida pelo IPCA diretamente do Site do Banco Central a partir do pacote rbcb. O código abaixo exemplifica.
ipca <- get_series(433, start_date = as.Date('01/01/2007',
format = "%d/%m/%Y"))
Observe que estamos pegando os dados da série 433 (da inflação) a partir de janeiro de 2007. Isso é proposital, posto que há diversos problemas com a série antes desse período, que precisaríamos limpar a partir de uma análise exploratória dos dados. Estamos supondo aqui que essa etapa já foi cumprida. Na sequência, nós investigamos justamente a característica sazonal da inflação no Brasil.
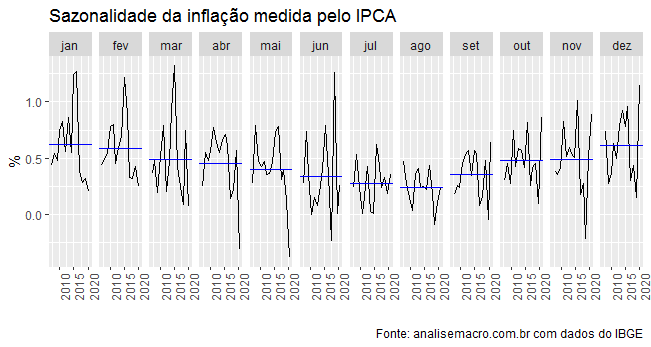
ipca = ipca %>% mutate(date = yearmonth(date)) %>% rename(vmensal = `433`) %>% as_tsibble(index=date) ipca %>% gg_subseries(vmensal)+ labs(x='', y='%', title='Sazonalidade da inflação medida pelo IPCA', caption='Fonte: analisemacro.com.br com dados do IBGE')
Observe que a média mensal da inflação medida pelo IPCA cai ao longo do primeiro semestre e vai gradativamente aumentando ao longo do segundo. Esse comportamento está intimamente relacionado ao comportamento do processo produtivo ao longo do ano.
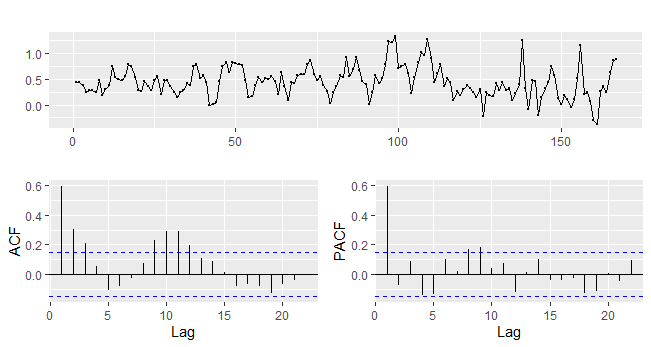
Uma vez que, portanto, diagnosticamos o efeito sazonal da inflação, precisaremos incluir isso na nossa modelagem. Antes de prosseguir, por suposto, vamos dar uma olhada no gráfico da série e nas funções de autocorrelação. Para isso, usamos a função ggtsdisplay do pacote forecast.
ggtsdisplay(ipca$vmensal)
Para fins de modelagem, vamos considerar que a inflação medida pelo IPCA é uma série estacionária e que os termos que a melhor descrevem, conforme os gráficos ACF e PACF são representados por um modelo SARIMA . Com base nisso, nós estimamos o modelo SARIMA a partir da função Arima também do pacote forecast. Além disso, também estimamos um modelo automático com a função auto.arima. O código abaixo implementa.
### Modelos inflacao_mensal = ts(ipca$vmensal, start=c(2007,01), freq=12) auto <- auto.arima(inflacao_mensal, max.p=5, max.q=5, max.P=5, max.Q=5) sarima <- Arima(inflacao_mensal, order=c(1,0,0), seasonal = c(0,0,1))
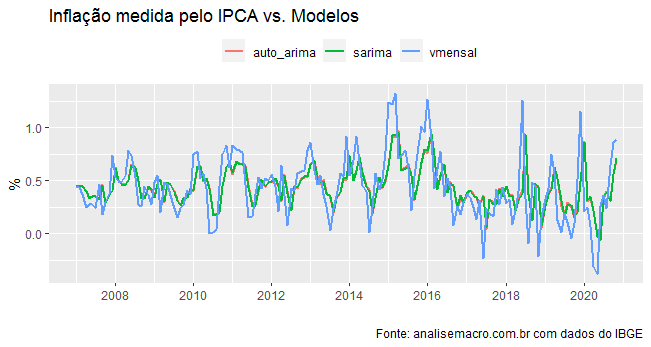
Abaixo, comparamos o ajuste dos modelos estimados.
ipca =
ipca %>%
mutate(auto_arima = fitted(auto),
sarima = fitted(sarima))
ipca %>%
gather(variavel, valor, -date) %>%
ggplot(aes(x=date, y=valor, colour=variavel))+
geom_line(size=.8)+
theme(legend.title = element_blank(),
legend.position = 'top')+
scale_x_date(breaks = date_breaks('2 year'),
labels = date_format("%Y"))+
labs(x='', y='%',
title='Inflação medida pelo IPCA vs. Modelos',
caption='Fonte: analisemacro.com.br com dados do IBGE')
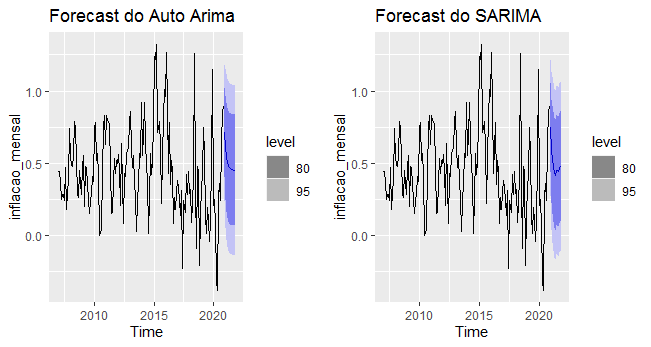
Uma vez que tenhamos construído o nosso modelo SARIMA, podemos utilizá-lo para fins de previsão. O código abaixo implementa uma previsão de 12 meses.
fauto <- forecast(auto, h=12) fsarima <- forecast(sarima, h=12)
O gráfico abaixo ilustra a previsão gerada pelos modelos.
Curtiu? O exercício acima faz parte do nosso Curso de Análise de Séries Temporais, que cobre uma introdução a modelos univariados e multivariados de séries temporais, com diversas aplicações feitas com o R. Confira e veja se é adequado para você! Até o próximo exercício!
_____________________