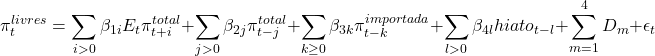O objetivo do post de hoje será mostrar como o R pode nos auxiliar a estimar uma forma reduzida da Curva de Phillips com a imposição da restrição de verticalidade de longo prazo estimada com instrumentos para o Brasil. O modelo segue uma versão simplificada do apresentado pelo Boxe do RI 2018/09
A Curva de Phillips para a inflação de preços livres do Brasil é representada por:
com a imposição da restrição de verticalidade de longo prazo:
onde é a inflação de preços livres do IPCA;
é a expectativa em t acerca da inflação do IPCA i trimestres à frente;
é a inflação do IPCA;
é uma medida da inflação importada;
é uma medida do hiato do produtos;
são Dummys de choques e
um termo de erro.
Basicamente, a inflação dos preços livres é uma função linear da inflação passada, das expectativas de inflação, do hiato do produto e da inflação importada. Os dados são trimestrais.
Para estimarmos a Curva de Phillips iremos passar por todas as etapas do processo de análise de dados utilizando o R, iremos coletar os dados, realizar os devidos tratamentos, e por fim iremos estimar a equação por meio de uma regressão em dois estágios com a restrição utilizando o pacote {systemfit}.
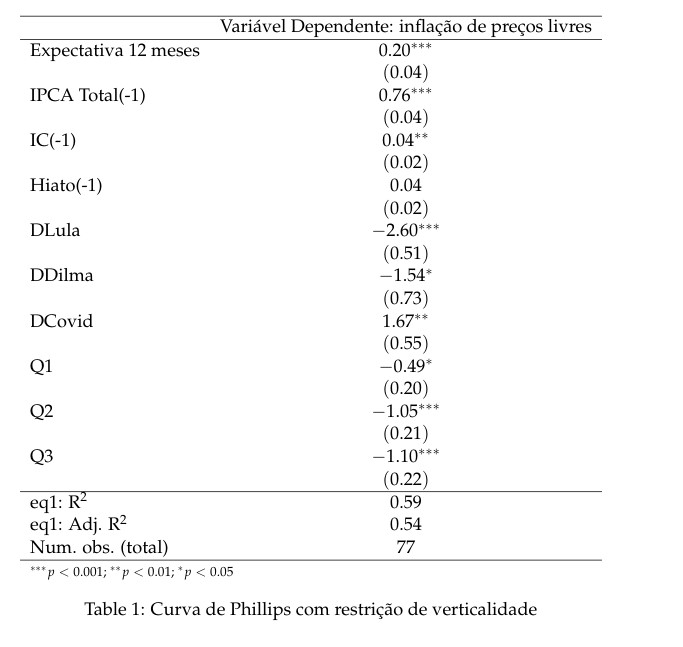
Abaixo, os resultados Modelo com os coeficientes e as principais estatísticas.
_____________________________________
Quer aprender mais?
Seja um aluno da nossa trilha de Macroeconomia Aplicada e aprenda a criar projetos voltados para a Macroeconomia.