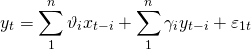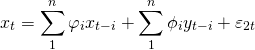[et_pb_section admin_label="section"][et_pb_row admin_label="row"][et_pb_column type="4_4"][et_pb_text admin_label="Texto" background_layout="light" text_orientation="justified" text_font="Verdana||||" text_font_size="18" use_border_color="off" border_color="#ffffff" border_style="solid"]
Em uma economia aberta com governo, sabemos que a poupança doméstica não necessariamente será igual à taxa de investimento. Isto porque, se um determinado país investe mais do que poupa, ele pode recorrer à poupança externa, o que resulta em saldo negativo na conta corrente. Com efeito, sua conta de capital no balanço de pagamentos terá saldo positivo, refletindo essa necessidade de capital estrangeiro. Isso dito, um país que poupa pouco terá que necessariamente conviver com déficit em conta corrente, arcando com toda a sorte de consequências que isso implica. Certo?
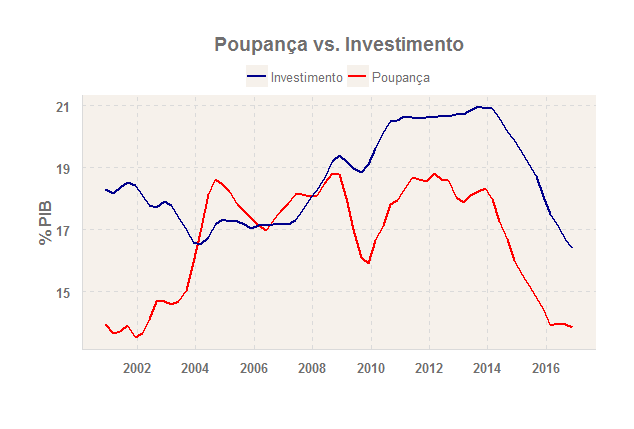
Muito bem. Então, imagine que estejamos agora interessados em verificar empiricamente a relação entre poupança doméstica e investimento. Existem algumas teorias na prateleira, bastante conhecidas, mas nós queremos verificar isso na prática. Para isso, nós podemos pegar os dados da poupança e do investimento nas Contas Nacionais Trimestrais do IBGE, ambas acumuladas em quatro trimestres e controladas pelo PIB. O gráfico abaixo ilustra as mesmas.
Com os dados em mãos, poderíamos agora efetuar um teste de precedência temporal, como o Teste de Granger, sobre as séries, para entender melhor como elas se relacionam. O Teste de Granger pode ser explicado como se segue. Se valores passados de nos ajudam a prever
, então diz-se que
Granger causa
. De maneira formal,
(1)
Se , ou seja, se todos
são conjuntamente diferentes de zero, então temos que
. O caso contrário:
(2)
Onde, se valer que , poderemos concluir que
Granger causa
. O problema, como aponta He e Maekawa (2001) é que o Teste de Granger pode ser inconsistente na presença de processos integrados. Nesses casos, a literatura tem recomendado adotar o procedimento descrito em Toda e Yamamoto (1995).
Os resultados da aplicação do procedimento de Toda-Yamamoto sugerem que existe causalidade na direção da poupança para o investimento, enquanto não se pode rejeitar a hipótese nula no caso contrário. E agora? Bom, agora é voltar para a teoria... 🙂
_____________________________________
[/et_pb_text][et_pb_button admin_label="Botão" button_url="https://analisemacro.com.br/cursos-de-r/macroeconometria/" url_new_window="off" button_text="Gostou? Esse Exercício faz parte da Seção 12 do nosso Curso de Macroeconometria usando o R! " button_alignment="center" background_layout="light" custom_button="off" button_letter_spacing="0" button_use_icon="default" button_icon_placement="right" button_on_hover="on" button_letter_spacing_hover="0" /][et_pb_image admin_label="Imagem" src="https://analisemacro.com.br/wp-content/uploads/2016/11/macroeconometria.png" show_in_lightbox="off" url="https://analisemacro.com.br/cursos-de-r/macroeconometria/" url_new_window="off" use_overlay="off" animation="left" sticky="off" align="center" force_fullwidth="off" always_center_on_mobile="on" use_border_color="off" border_color="#ffffff" border_style="solid" /][/et_pb_column][/et_pb_row][/et_pb_section]