Em outubro do ano passado o Instituto Nacional de Pesquisa Economica (NIER) da Suécia publicou um working paper onde eles tentam avaliar os efeitos da incerteza política americana sobre a taxa de crescimento do PIB sueco. Para isso, usaram o Policy Uncertainty Index (PUI) que, colocado de maneira bem simples, leva em consideração a frequência com que notícias relacionadas a politica monetária e fiscal aparecem nos jornais, prazos de expiração de leis relacionadas a imposto e divergências entre previsão de inflação (por parte do mercado) e compras governamentais.
Achei o tema bem interessante e resolvi tentar reproduzir o trabalho deles para dados brasileiros. Primeiramente, acho interessante destacar, novamente, o pacote BMR que possibilita a estimação de alguns tipos de BVARs, mais especificamente ele nos deixa estimar exatamente o mesmo tipo de BVAR utilizado no artigo acima. Além disso, acho legal destacar a importância de pacotes como estes que possibilitam a estimação de modelos complexos que requerem um enorme conhecimento de programação (sem falar de matemática e estatística). Apesar do crescente interesse em métodos Bayesianos, são poucos os softwares que incorporam isso (o Eviews, por exemplo, só incluiu estes modelos em sua oitava versão). Para os interessados recomendo fortemente a vignette do pacote BMR.
Dito isto, trata-se de um steady state prior BVAR* e, em poucas palavras, o que diferencia ele de um BVAR tradicional é que ele nos permite a não só incluir informações a priori sobre os coeficientes que queremos estimar mas também sobre as médias condicionais das séries que utilizamos, ou seja, o que acreditamos serem seus valores de steady state.
Vamos agora para o que interessa. Os dados utilizados são a taxa de variação do PIB trimestral com ajuste sazonal (trimestre contra mesmo trimestre do ano anterior) e o Policy Uncertainty Index entre o primeiro trimestre de 1996 e o terceiro trimestre de 2014. Como o índice de incerteza é mensal eu agreguei da mesma forma que em Stockhammar e Österholm (2014)**, isto é, a média de 3 meses do índice representa um trimestre. Abaixo um gráfico (Ah! Todos os gráficos foram produzidos com o próprio pacote BMR) com os dados utilizados e o código necessário.
dates <- seq(as.Date('1997-03-01'),
as.Date('2014-09-1'),
by = '3 months')
gtsplot(model.data, dates=dates)
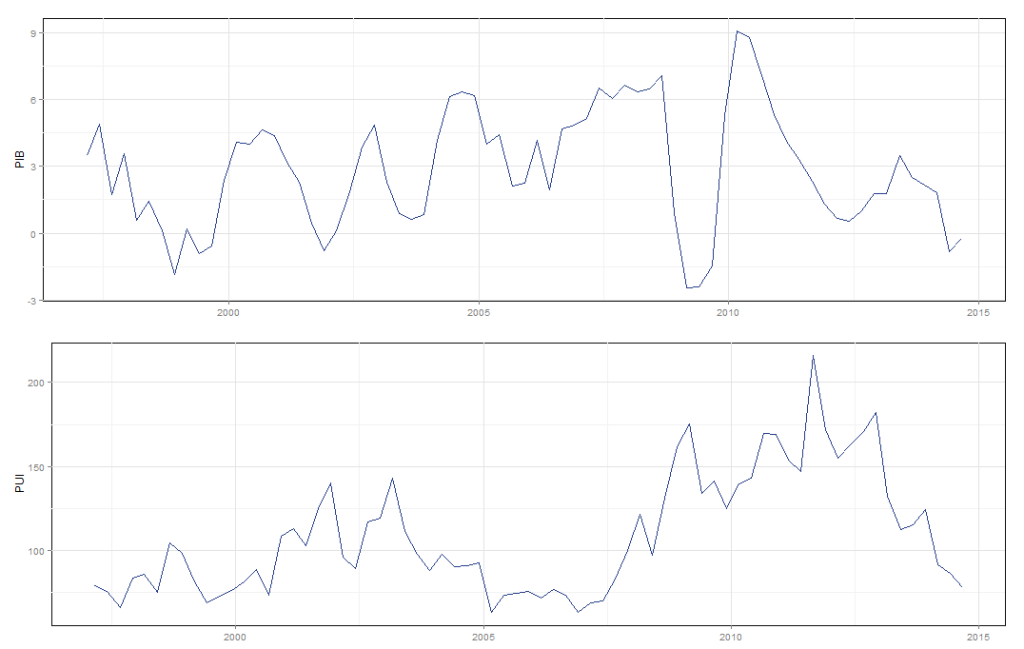
De modo a determinar a informação a priori sobre os coeficientes eu utilizei os correlogramas das duas séries enquanto que para o steady state eu simplesmente calculo as médias de ambas as séries. A média da variação trimestral do PIB é de aproximadamente 0.7 enquanto que a média do índice é de aproximadamente 107.6. O gráfico com as funções de correlação são apresentadas abaixo (e os códigos também, obviamente).
gacf(model.data, save=F) gpacf(model.data, save=F)
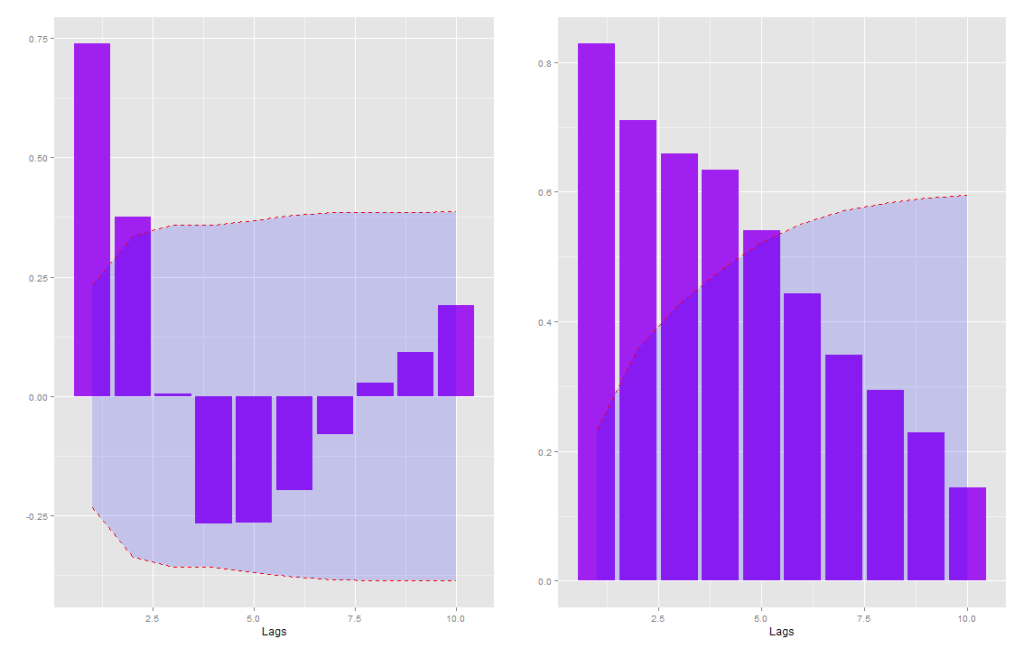
Desta forma, usamos como informação, para os coeficientes de primeira ordem, 0.74 para o PIB e 0.8 para o PUI.
Uma pequena diferença entre a minha abordagem e a feita em Stockhammar e Österholm (2014) é que eles estimam um BVAR restrito, onde assumem que, dado que a Suécia é uma pequena economia, flutuações em seu PIB não afetam o indíce. Isto é, no sistema de equações, a defasagem do PIB tem coeficiente igual a zero na equação do PUI. Ou seja, estimamos
porém assumimos que .
Infelizmente, até o momento não é possível (pelo menos que eu saiba) fazer este tipo de restrição pela função BVARS (função do pacote BMR que estima modelos BVAR de steady state prior). Porém, é possível especificar alguns parâmetros da matriz de covariância a priori dos coeficientes. Portanto, de modo a contornar o problema de não conseguir restringir os parâmetros, eu defino o valor destas defasagens como sendo iguais a zero e com uma dispersão baixa (para isso utilizo um valor baixo para o input HP1), assim forçando as estimativas a ficarem bem centradas.
Bom, feito isto podemos finalmente estimar o modelo e visualizar as funções de resposta ao impulso. Código e resultados seguem abaixo.
bvars <- BVARS(model.data, psiprior=colMeans(model.data),
coefprior=c(0.75,0.8),p=4,
irf.periods=24,keep=50000,burnin=10000,
XiPsi=1,HP1=0.001,HP4=2,gamma=NULL)
IRF(bvars, save=F, percentiles=c(.05, .50,.95))
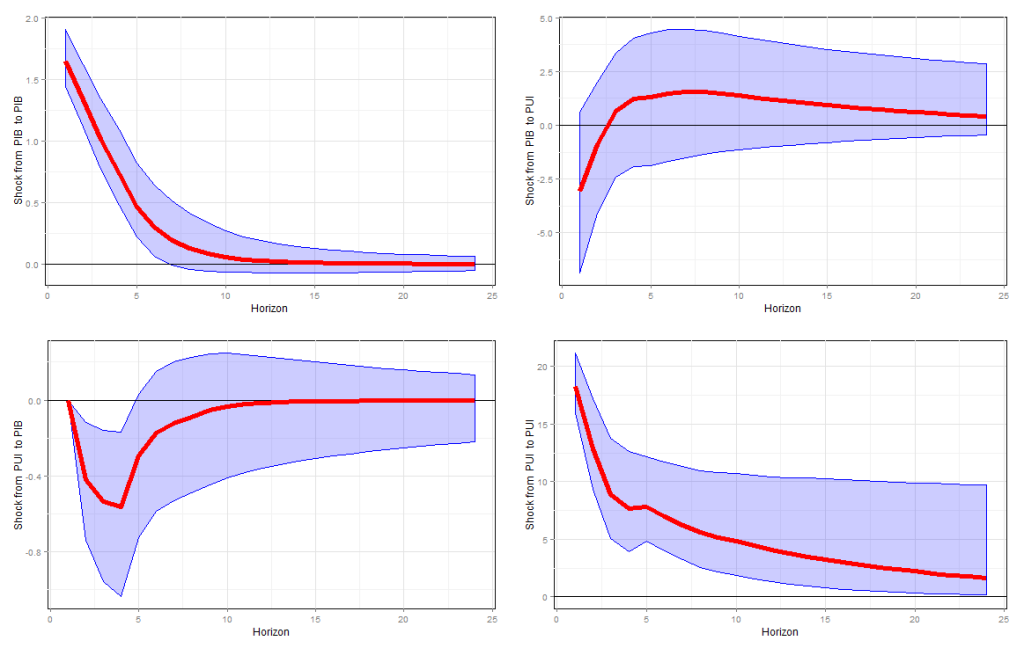
Como podemos ver, um choque a taxa de variação do PIB brasileiro não tem efeitos estatisticamente significantes ao índice, porém o contrário não é verdadeiro. Neste caso, isto é quando induzimos um choque de incerteza (ou seja, um choque positivo ao índice), o PIB responde de maneira negativa, com o pico desse efeito sendo repassado depois de aproximadamente 3 trimestres e tendo sua duração de aproximadamente 1 ano.
Portanto, este curto exercício mostra que a economia brasileira é afetada negativamente pelas incertezas advindas da economia americana. Em Stockhammar e Österholm (2014) os autores, de forma a testarem a robustez dos resultados, incluem mais variáveis ao modelo. Deixo essa parte para os leitores mais interessados.
* Desenvolvido em Villani, M. (2009). Steady‐state priors for vector autoregressions. Journal of Applied Econometrics, 24(4), 630-650.
** Stockhammar, P., & Österholm, P. (2014). Effects of US Policy Uncertainty on Swedish GDP Growth (No. 135)

