Resumo

Este exercício examina o problema de fim de amostra, uma limitação comum em estimativas do hiato do produto baseadas em métodos univariados e bidirecionais. A análise é conduzida por meio de estimativas em quase tempo real, implementadas na linguagem de programação R.

Introdução

O termo “problema de fim de amostra” (ou “end-of-sample problem”, em inglês) deriva diretamente da sua natureza: ele ocorre nas extremidades (especialmente no final) de uma série temporal, onde a falta de dados futuros afeta a estimação da tendência e, consequentemente, do hiato do produto (diferença entre o PIB observado e o PIB potencial). O termo reflete o desafio de estimar componentes como a tendência ou o ciclo quando a amostra disponível é limitada, especialmente em métodos que dependem de informações de toda a série.

No contexto do hiato do produto, o problema ganha relevância devido a dois fatores principais:

• Métodos bidirecionais, como o Filtro de Hodrick-Prescott (HP), utilizam dados passados e futuros para suavizar a tendência em cada ponto t. Próximo ao fim da amostra (ex.: último trimestre disponível), a falta de observações futuras distorce a tendência e o hiato estimados.
• Aplicações em tempo real ou quase real: Nessas situações, as distorções podem resultar em revisões significativas do hiato à medida que novos dados surgem, criando desafios práticos para formuladores de políticas econômicas.

Diante disso, surgem duas abordagens possíveis: corrigir os métodos suscetíveis ao problema de fim de amostra ou buscar alternativas que o evitem. Uma solução potencial seria incorporar previsões do PIB (de agentes de mercado ou modelos proprietários) para estender a série além do último ponto disponível, aumentando a quantidade de dados futuros. Contudo, essa estratégia introduz incertezas, pois depende da acurácia dessas previsões. Se elas se revelarem imprecisas, as estimativas do hiato serão igualmente comprometidas. Essa abordagem, embora promissora, não será explorada neste exercício, sendo reservada para exercícios futuros.

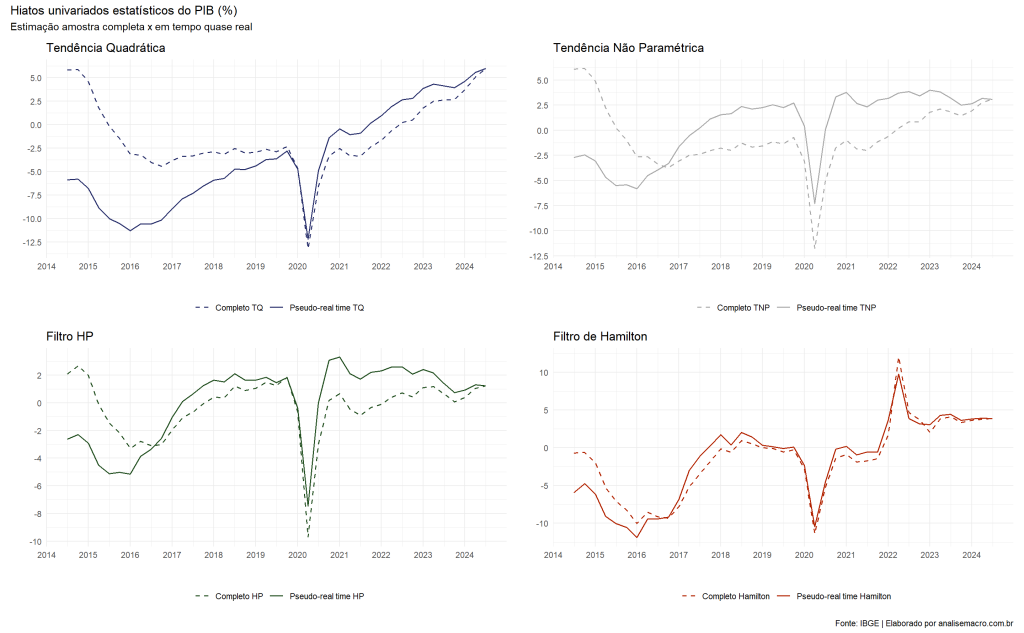
O foco aqui é analisar o problema de fim de amostra em diferentes métodos de estimação do hiato. Para isso, comparamos estimativas baseadas na amostra completa — abrangendo todo o período disponível — com estimativas em quase tempo real (pseudo-real time). Estas últimas fixam o início da amostra no primeiro trimestre de 1996 e variam o ponto final, trimestre a trimestre, de 2014Q3 até 2024Q3. Por exemplo, o hiato em 2014Q3 é calculado usando apenas os dados do PIB até esse trimestre.

Métodos

Será utilizado quatro métodos de estimação do Hiato do Produto:

• Tendência Quadrática
• Tendência Não Paramétrica
• Filtro Hodrick-Prescott (HP)
• Filtro de Hamilton

Abaixo, seguem as metodologias:

1. Tendência Quadrática

Este método assume que o PIB potencial segue uma função quadrática no tempo, modelada por uma regressão polinomial de segundo grau. É simples e amplamente usado, mas pode ser inflexível para capturar mudanças estruturais ou não linearidades em séries econômicas.

onde:
- : PIB observado no tempo ,
- : coeficientes estimados por regressão de mínimos quadrados ordinários (OLS),
- : hiato ou componente cíclico.

O hiato é dado por:

(em percentual).

Sofre do problema de fim de amostra, pois os coeficientes são estimados com toda a série, e pontos finais podem distorcer a tendência devido a choques recentes ou falta de dados futuros.

Tendência Não Paramétrica (Smoothing por Regressão Localmente Ponderada)

Este método utiliza uma suavização não paramétrica por regressão localmente ponderada (como o LOESS, Local Regression). A tendência é calculada como uma previsão ponderada usando um subconjunto de observações próximas a , com pesos decrescentes baseados na distância temporal.

Para cada , seleciona um subconjunto de índices

até

onde

é o tamanho da série, e .

Os pesos para cada observação (de a ) seguem uma função trícube:

onde é o índice da observação .

A tendência suavizada é a previsão ponderada desse subconjunto. O ciclo é dado por:

O hiato é calculado como:

(em percentual).

Embora flexível, pode sofrer de problemas de fim de amostra se a janela de suavização for afetada pela falta de dados nas extremidades, embora menos intensamente que métodos paramétricos rígidos.

3. Filtro Hodrick-Prescott (HP)

Este é um método bidirecional amplamente utilizado para decompor séries temporais em tendência e ciclo, minimizando a soma dos quadrados dos desvios do PIB em relação à tendência, penalizando variações bruscas na tendência.

onde:
- : PIB observado,
- : tendência estimada,
- : parâmetro de suavidade (geralmente 1600 para dados trimestrais).

O primeiro termo minimiza o erro entre o PIB e a tendência, e o segundo penaliza mudanças abruptas na tendência.

O hiato é dado por:

Sofre do problema de fim de amostra, pois é bidirecional, dependendo de dados futuros para suavizar a tendência. Perto do fim da amostra, a ausência de dados futuros distorce as estimativas, levando a revisões significativas em tempo real.

4. Filtro de Hamilton

Proposto por James D. Hamilton como alternativa ao Filtro HP, este método é unidirecional e baseado em regressão linear, prevendo com base em valores passados de . É projetado para evitar os problemas do HP, incluindo o de fim de amostra.

onde:

- : horizonte de previsão (ex.: 8 trimestres para dados trimestrais),
- : número de lags (ex.: 4 trimestres),
- : coeficientes estimados por OLS.

A tendência em é , e o ciclo é:

O hiato é:

onde o PIB potencial é derivado da tendência ajustada.

Diferente do Filtro HP e outras estimativas, o Filtro de Hamilton é unidirecional, usando apenas dados passados e presentes até para estimar a tendência. Isso evita distorções nas extremidades, pois não depende de informações futuras. No entanto, há um atraso de períodos para calcular o ciclo, pois requer para o erro . Em tempo real ou quase real, isso é uma limitação previsível, mas não uma distorção, tornando-o uma solução superior para evitar o problema de fim de amostra do HP.

Portanto, para a estimativa em quase tempo real, esperamos que o Filtro de Hamilton não tenha uma diferença considerável em relação a estimativa da amostra completa.

Estimativa

Utilizamos dados da série encadeada do índice de volume trimestral do PIB com ajuste sazonal, abrangendo o período de 1996Q1 até 2024Q3, obtidos no SIDRA/IBGE. O PIB é transformado em logaritmo para ser utilizado como entrada nos métodos de estimação. Após a aplicação dos métodos, a série tendencial é obtida revertendo a transformação logarítmica por meio da exponenciação, e o hiato do produto é calculado.

A análise é realizada em dois cenários: (i) estimando a tendência com a amostra completa e (ii) estimando em quase tempo real, onde os dados são considerados apenas até 2014Q3 inicialmente, e a cada nova observação disponível, o hiato é recalculado.

É importante destacar que o termo “quase tempo real” é utilizado porque os cálculos se baseiam na última vintage disponível dos dados do PIB. Caso a análise fosse feita com a vintage exata de cada momento histórico (ou seja, sem considerar as revisões subsequentes do IBGE), seria chamada de estimação em tempo real. Como o IBGE frequentemente revisa os valores do PIB, a série pode variar conforme o momento da coleta dos dados. Dessa forma, ao comparar estimativas baseadas em diferentes vintages, os valores do hiato podem diferir, justificando o uso do termo “quase tempo real”.

Os resultados estão apresentados na figura abaixo. Nota-se uma diferença considerável entre as estimativas de hiato, sendo a menor discrepância observada no Filtro de Hamilton, pois esse método foi projetado para minimizar o problema de fim de amostra.

Nota-se também a trajetória comum das séries ao fim da amostra, evidenciando que de fato existe o problema.