Como podemos compreender a taxa de juros para os tomadores de crédito? Neste artigo, desenvolvemos dois modelos com o objetivo de investigar a relação entre diversas variáveis que influenciam a flutuação da taxa de juros média para indivíduos. Todo o processo de coleta, análise e construção do modelo foi conduzido utilizando a linguagem de programação Python.
A taxa de juros para pessoa física é um indicador que reflete o custo do crédito para indivíduos. Ela desempenha um papel essencial na economia, influenciando o comportamento financeiro das pessoas e, por sua vez, impactando o funcionamento geral do mercado financeiro e o crescimento econômico.
A política monetária, estabelecida pelo banco central de um país, desempenha um papel crítico na determinação das taxas de juros. Alterações na taxa de juros de referência da economia, como a Taxa Selic no caso do Brasil, têm um efeito cascata ao longo da curva de juros. Isso significa que mudanças na taxa de juros oficial são repassadas para todas as faixas de prazos e modalidades de empréstimos e financiamentos.
Quando a taxa de juros sobe, o custo do crédito aumenta, tornando empréstimos e financiamentos mais caros para os tomadores, o que pode desencorajar o consumo e os investimentos. Por outro lado, quando as taxas de juros são reduzidas, o crédito se torna mais acessível e barato, estimulando a demanda por empréstimos e financiamentos, o que pode impulsionar o crescimento econômico.
Portanto, as flutuações na taxa de juros para pessoa física têm um impacto direto nas decisões financeiras dos indivíduos e nas condições gerais de crédito, desempenhando um papel importante na estabilidade e no crescimento da economia.
Neste exercício, buscamos identificar a variável mais significativa para explicar a variação da taxa média de juros para os tomadores de crédito (Pessoa Física). Investigamos se a variável “ex-post,” representada pela Taxa Selic, ou a variável “ex-ante,” representada pelo Swaps DI x pré 360 dias, desempenha um papel mais relevante. Além disso, examinamos o impacto relativo de cada taxa em vários níveis de defasagem.
Para o modelo, consideramos a seguinte equação:
![\[\Delta Juros^{tomador}_t = \alpha + \beta_1 \Delta Juros^{\text{referência}}_{t-j} + \beta_2 \Delta Inad_{t-k} + \beta_3 \Delta Incerteza_{t-l} + \epsilon_t\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-50999cbf41d2b6c1370a1736af9c8201_l3.png "Rendered by QuickLaTeX.com")
Em que:
: Variação da Taxa média de juros - recursos livres - pessoa física - total (SGS/BCB: 20740)
: Variação da Taxa de Juros de referências.
: Variação da Inadimplência - pessoa física - total (SGS/BCB: 21112)
: Variação do EMBI + Brasil.
: indicam defasagens utilizadas.
Os alunos do curso de Macroeconometria usando o Python, têm a oportunidade de adquirir um conhecimento abrangente em todas as fases do processo, desde a coleta e a preparação dos dados até a análise, o desenvolvimento de modelos econométricos e a comunicação dos resultados, tudo isso utilizando Python como ferramenta principal.
Visualização
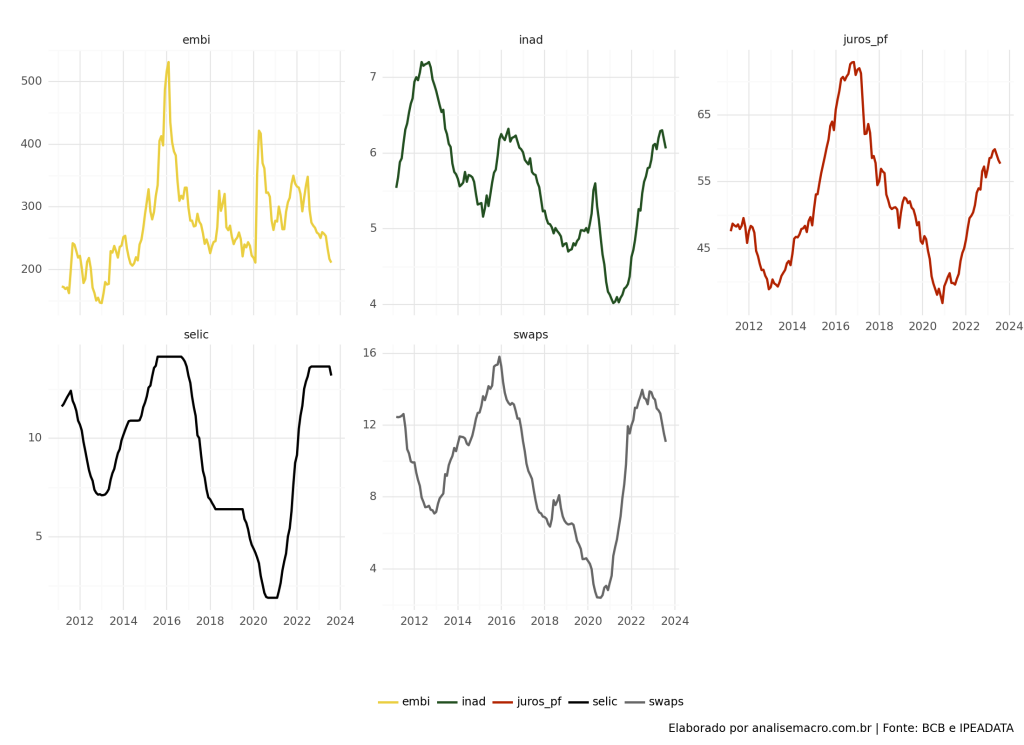
Podemos realizar uma breve analise das variáveis (em nível) através do gráfico abaixo. Vemos que há uma aparente correlação entre os juros e a inadimplência.
Modelo 1: Swap DI x Pré
Usamos a equação proposta para estimar uma regressão linear múltipla para verificar se o Swap DI x Pré 360 dias possui poder explicativo para o juros de pessoa física.
Código
OLS Estimation Summary
==============================================================================
Dep. Variable: juros_pf R-squared: 0.2087
Estimator: OLS Adj. R-squared: 0.1592
No. Observations: 137 F-statistic: 44.132
Date: Mon, Nov 06 2023 P-value (F-stat) 0.0000
Time: 11:54:02 Distribution: chi2(8)
Cov. Estimator: robust
Parameter Estimates
===============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
-------------------------------------------------------------------------------
Intercept 0.0370 0.1090 0.3392 0.7345 -0.1766 0.2506
swaps_lag3 0.8149 0.2812 2.8982 0.0038 0.2638 1.3661
swaps_lag6 -0.0341 0.2561 -0.1332 0.8940 -0.5361 0.4679
swaps_lag9 0.4765 0.2549 1.8696 0.0615 -0.0230 0.9760
swaps_lag12 0.7329 0.2250 3.2573 0.0011 0.2919 1.1740
embi_lag 0.0026 0.0052 0.4948 0.6208 -0.0077 0.0129
inad_lag1 -0.5814 1.0869 -0.5349 0.5927 -2.7118 1.5490
inad_lag2 -0.4676 0.9927 -0.4710 0.6376 -2.4133 1.4781
inad_lag3 -0.2000 0.9811 -0.2039 0.8384 -2.1229 1.7228
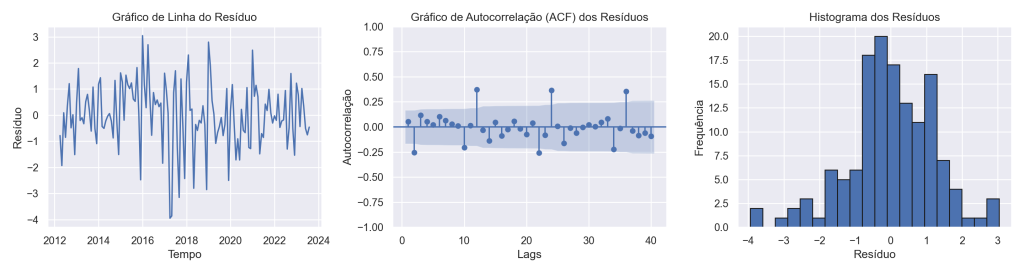
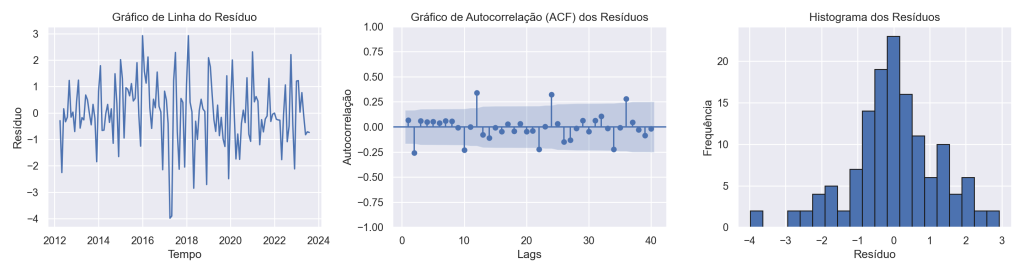
===============================================================================Verificamos os resíduos da regressão por meio de uma breve análise gráfica.
Modelo 2: Selic
Realizamos o mesmo procedimento para a equação, tomando como variável de juros referencia a Taxa Selic.
Código
OLS Estimation Summary
==============================================================================
Dep. Variable: juros_pf R-squared: 0.2302
Estimator: OLS Adj. R-squared: 0.1820
No. Observations: 137 F-statistic: 47.326
Date: Mon, Nov 06 2023 P-value (F-stat) 0.0000
Time: 11:54:02 Distribution: chi2(8)
Cov. Estimator: robust
Parameter Estimates
===============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
-------------------------------------------------------------------------------
Intercept 0.0183 0.1073 0.1704 0.8647 -0.1920 0.2285
selic_lag3 1.6851 0.5397 3.1225 0.0018 0.6274 2.7428
selic_lag6 0.1224 0.6254 0.1957 0.8448 -1.1034 1.3482
selic_lag9 -0.1186 0.5789 -0.2049 0.8376 -1.2532 1.0160
selic_lag12 0.4975 0.4484 1.1095 0.2672 -0.3814 1.3764
embi_lag 0.0038 0.0052 0.7351 0.4623 -0.0063 0.0140
inad_lag1 -0.6102 1.0339 -0.5901 0.5551 -2.6365 1.4162
inad_lag2 -1.0238 1.0446 -0.9801 0.3270 -3.0712 1.0236
inad_lag3 -0.3901 0.9115 -0.4280 0.6687 -2.1767 1.3964
===============================================================================
Comparação dos Modelos
Por fim, podemos comparar os resultados dos dois modelos.
Código
Model Comparison
==========================================
reg1 reg2
------------------------------------------
Dep. Variable juros_pf juros_pf
Estimator OLS OLS
No. Observations 137 137
Cov. Est. robust robust
R-squared 0.2087 0.2302
Adj. R-squared 0.1592 0.1820
F-statistic 44.132 47.326
P-value (F-stat) 5.372e-07 1.329e-07
================== =========== ===========
Intercept 0.0370 0.0183
(0.3392) (0.1704)
swaps_lag3 0.8149
(2.8982)
swaps_lag6 -0.0341
(-0.1332)
swaps_lag9 0.4765
(1.8696)
swaps_lag12 0.7329
(3.2573)
embi_lag 0.0026 0.0038
(0.4948) (0.7351)
inad_lag1 -0.5814 -0.6102
(-0.5349) (-0.5901)
inad_lag2 -0.4676 -1.0238
(-0.4710) (-0.9801)
inad_lag3 -0.2000 -0.3901
(-0.2039) (-0.4280)
selic_lag3 1.6851
(3.1225)
selic_lag6 0.1224
(0.1957)
selic_lag9 -0.1186
(-0.2049)
selic_lag12 0.4975
(1.1095)
------------------------------------------
T-stats reported in parenthesesQuer aprender mais?
Clique aqui para fazer seu cadastro no Boletim AM e baixar o código que produziu este exercício, além de receber novos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas diretamente em seu e-mail.
