Nesse exercício, verificamos a relação entre o índice de volatilidade (VIX) e a taxa de câmbio. A ideia básica, é a de que, a volatilidade, e portanto, a incerteza do mercado gera mudanças significativas sobre o preço do câmbio. Fazemos o uso do procedimento de Toda-Yamamoto para investigar essa relação usando o Python como ferramenta.
De forma a analisar essa suposição, devemos investigar através de uma análise de dados, os possíveis acontecimentos que ocasionaram mudanças em variáveis que descrevem a dinâmica de precedência temporal.
Feito a análise de dados, podemos prosseguir para verificar se, de fato, existe influência do índice de volatilidade no comportamento da taxa de câmbio. Para isso, vamos executar o procedimento de Toda-Yamamoto.
1. Carregamento de bibliotecas
import pandas as pd import pandas_datareader.data as web import datetime from plotnine import * from bcb import sgs import statsmodels.api as sm # modelagem from statsmodels.tsa.api import VAR # Vetores Autoregressivos from statsmodels.tsa.stattools import adfuller
2. Análise de Dados
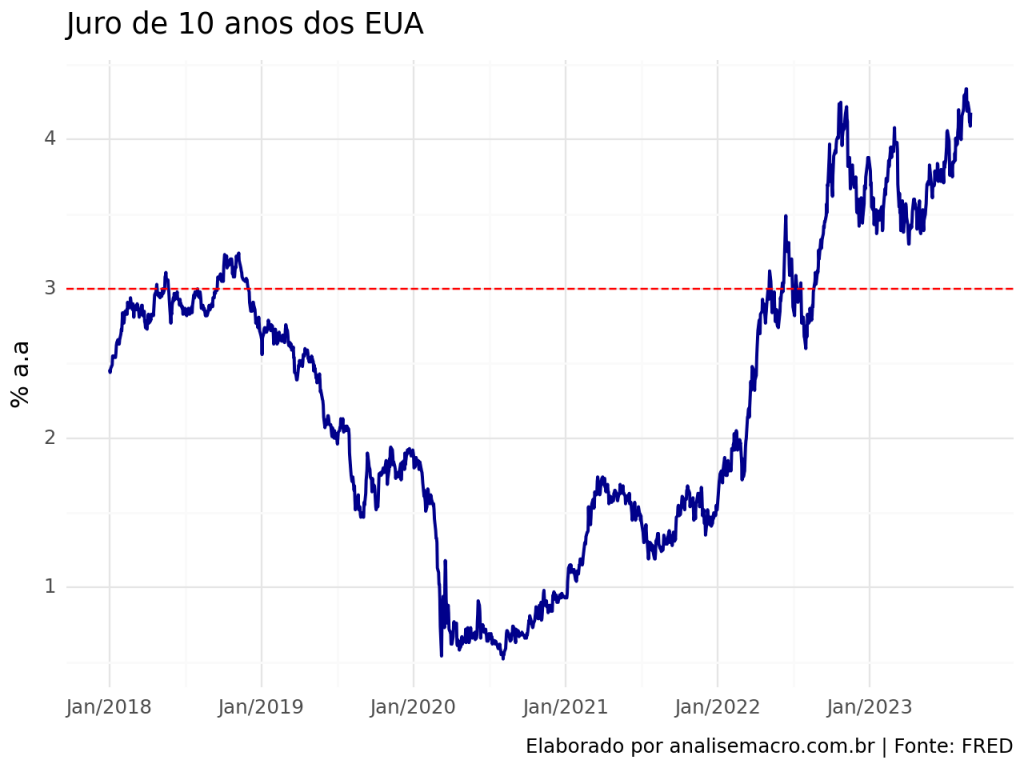
2.1 Juro de 10 anos dos Estados Unidos
No últimos anos, vimos uma intensa mudança de preços nos mercados internacionais em resposta, principalmente, de choques de oferta, proporcionados pela pandemia e Invasão da Ucrânia pela Rússia.
Eventos subsequentes seguirão com as respostas dos Bancos Centrais para apaziguar a escalada das taxas de inflação, gerando a preocupação, se, no futuro haverá ou não um “soft landing”.
O juro de 10 anos dos Estados Unidos abriu o ano de 2022 com uma tendência positiva, dando sinais de que romperia a barreira “psicológica” de 3% a.a.. Além de ocorrer, houve a persistência da taxa no valor acima de 4% a.a. em 2023, devido às preocupações com a economia norte-americana e chinesa.
Vemos abaixo como analisar o gráfico do Juro de 10 anos do EUA usando o Python.
# Define as datas de início e fim start = datetime.datetime(2018, 1, 1) end = datetime.datetime(2023, 9, 1) # Captura os dados treasuries = web.DataReader(['DGS10'], 'fred', start, end).dropna().reset_index()
treasuries
| DATE | DGS10 | |
|---|---|---|
| 0 | 2018-01-02 | 2.46 |
| 1 | 2018-01-03 | 2.44 |
| 2 | 2018-01-04 | 2.46 |
| 3 | 2018-01-05 | 2.47 |
| 4 | 2018-01-08 | 2.49 |
| ... | ... | ... |
| 1414 | 2023-08-28 | 4.20 |
| 1415 | 2023-08-29 | 4.12 |
| 1416 | 2023-08-30 | 4.12 |
| 1417 | 2023-08-31 | 4.09 |
| 1418 | 2023-09-01 | 4.18 |
1419 rows × 2 columns
(ggplot(treasuries) + aes(x = 'DATE', y = 'DGS10') + geom_line(size = .8, color = "darkblue") + geom_hline(yintercept = 3, colour = 'red', linetype = "dashed") + scale_x_date(date_breaks = '1 years', date_labels = '%b/%Y') + theme(axis_text_x = element_text(angle = 45, hjust = 1)) + labs(title = "Juro de 10 anos dos EUA", caption = "Elaborado por analisemacro.com.br | Fonte: FRED", y = "% a.a", x = "") + theme_minimal() )
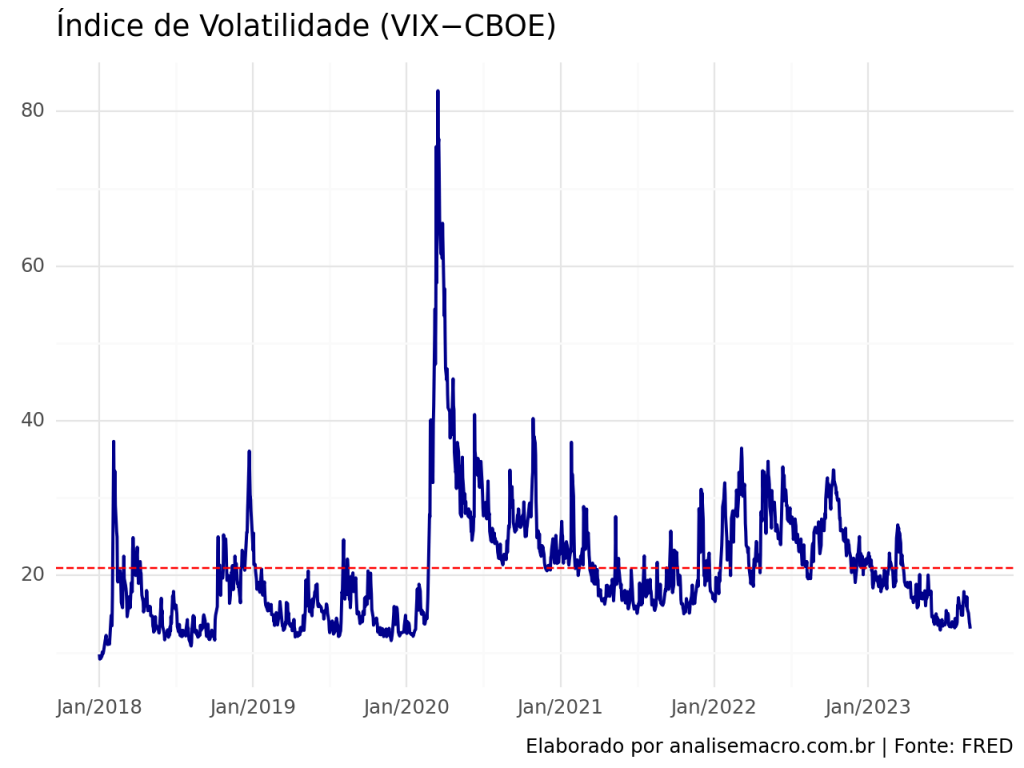
2.2 Índice de Volatilidade (VIX−CBOE)
Simultaneamente a elevação do Juro de 10 anos no EUA em 2018, vimos a ocorrência da elevação no índice de volatilidade VIX do CBOE. Ao passo que até anteriormente à pandemia de COVID, tivemos uma tendência de baixa de ambas as variáveis, período no qual o VIX encontrava-se abaixo de sua média histórica.
Entretanto, a partir da pandemia, com a elevação do VIX, o Juro de 10 anos teve um movimento contrário, devido as adversidades proporcionadas pelos choques.
E que apesar de queda significativa do VIX de 2022 até 2023, vimos um movimento contrário altista nos Juros de 10 anos.
# Captura os dados vix = web.DataReader(['VIXCLS'], 'fred', start, end).dropna().reset_index() vix
| DATE | VIXCLS | |
|---|---|---|
| 0 | 2018-01-02 | 9.77 |
| 1 | 2018-01-03 | 9.15 |
| 2 | 2018-01-04 | 9.22 |
| 3 | 2018-01-05 | 9.22 |
| 4 | 2018-01-08 | 9.52 |
| ... | ... | ... |
| 1432 | 2023-08-28 | 15.08 |
| 1433 | 2023-08-29 | 14.45 |
| 1434 | 2023-08-30 | 13.88 |
| 1435 | 2023-08-31 | 13.57 |
| 1436 | 2023-09-01 | 13.09 |
1437 rows × 2 columns
(ggplot(vix) + aes(x = 'DATE', y = 'VIXCLS') + geom_line(size = .8, colour = "darkblue") + geom_hline(yintercept = vix.VIXCLS.mean(), colour = 'red', linetype = "dashed") + scale_x_date(date_breaks = '1 years', date_labels = '%b/%Y') + theme(axis_text_x = element_text(angle = 45, hjust = 1)) + labs(title = "Índice de Volatilidade (VIX−CBOE)", caption = "Elaborado por analisemacro.com.br | Fonte: FRED", y = "", x = "") + theme_minimal() )
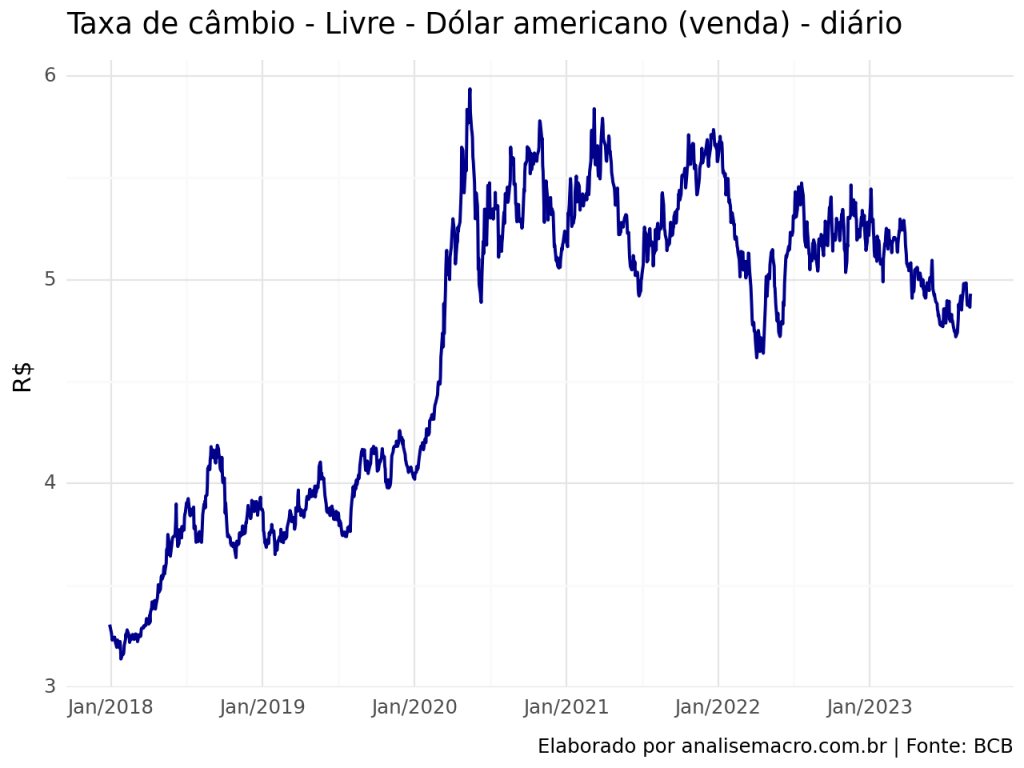
2.3 Taxa de câmbio - Livre - Dólar americano (venda) - diário
Os efeitos no VIX e taxas de Juros no EUA ocorridos durante a pandemia de COVID também podem ser verificados na taxa de câmbio, com ampla desvalorização da moeda brasileira.
Ao passo que em 2023, havia uma tendência de queda, concomitante a queda do VIX, a tendência altista dos Juros de 10 anos não permitiu essa desvalorização acentuada.
cambio = sgs.get({'cambio' : 1}, start = start, end = end).reset_index()
cambio
| Date | cambio | |
|---|---|---|
| 0 | 2017-12-29 | 3.3080 |
| 1 | 2018-01-02 | 3.2697 |
| 2 | 2018-01-03 | 3.2535 |
| 3 | 2018-01-04 | 3.2318 |
| 4 | 2018-01-05 | 3.2409 |
| ... | ... | ... |
| 1421 | 2023-08-28 | 4.8938 |
| 1422 | 2023-08-29 | 4.8706 |
| 1423 | 2023-08-30 | 4.8653 |
| 1424 | 2023-08-31 | 4.9219 |
| 1425 | 2023-09-01 | 4.9318 |
1426 rows × 2 columns
(ggplot(cambio) + aes(x = 'Date', y = 'cambio') + geom_line(size = .8, colour = "darkblue") + scale_x_date(date_breaks = '1 years', date_labels = '%b/%Y') + theme(axis_text_x = element_text(angle = 45, hjust = 1)) + labs(title = "Taxa de câmbio - Livre - Dólar americano (venda) - diário", caption = "Elaborado por analisemacro.com.br | Fonte: BCB", y = "R$", x = "") + theme_minimal() )
3. Procedimento de Toda-Yamamoto
O procedimento Toda-Yamamoto é baseado no conceito de causalidade de Granger, que postula que uma variável X “causa” (no sentido granger) outra variável Y se as informações passadas de X ajudarem a prever melhor Y do que apenas as informações passadas de Y. O teste de Toda-Yamamoto é uma extensão do teste de causalidade de Granger, que leva em consideração a presença de tendências e estruturas não lineares nas séries temporais.
Em caso de não estacionariedade de uma ou mais séries envolvidas no Teste de Granger, é possível que os resultados encontrados sejam espúrios. Nesses casos, um procedimento mais abrangente para ver a relação entre variáveis foi estabelecido na literatura por Toda e Yamamoto (1995). Para ilustrar o procedimento, vamos considerar as séries da Taxa de juros de 10 anos do EUA, o índice de volatilidade (VIX) e Taxa de câmbio - Livre - Dólar americano (venda) - diário.
O procedimento descrito por Toda e Yamamoto (1995) consiste, basicamente, nos seguintes passos:
- Verificar a ordem de integração das variáveis através de testes de raiz unitária e estacionariedade;
- Definir a ordem máxima (m) de integração entre as variáveis;
- Montar o VAR em nível para as variáveis;
- Determinar a ordem de defasagem do VAR(p) pelos critérios de informação tradicionais;
- Ver a estabilidade do modelo, em particular problemas de autocorrelação;
- Se estiver tudo certo, adicionar m defasagens ao VAR, de modo que você terá um VAR(p+m);
- Rodar o teste de Wald com p coeficientes e p graus de liberdade.
3.1. Tratamento dos dados
Antes de prosseguir com a montagem do VAR, devemos realizar alguns tratamentos em nossas variáveis.
Renomeamos a coluna de data, de forma que possamos unir os data frames pela mesma coluna (Date).
</pre>
# Renomeia as colunas
vix.rename(columns = {'DATE' : 'Date'}, inplace = True)
treasuries.rename(columns = {'DATE' : 'Date'}, inplace = True)
# Junta os dados
dados = vix.merge(cambio, on = 'Date')
dados = dados.merge(treasuries, on = 'Date').set_index('Date')
<pre>
3.2 Aplicação do Procedimento
Uma vez criado o Data Frame, devemos prosseguir com os passos elencados anteriormente.
1) Verificar a ordem de integração das variáveis através de testes de raiz unitária e estacionariedade.
O código e o resultado abaixo entrega o teste ADF de forma prática.
def adfuller_test(dataframe, signif=0.05, verbose=False):
"""Realiza o teste ADFuller para verificar a estacionaridade das colunas de um DataFrame e imprime o relatório"""
for coluna in dataframe.columns:
series = dataframe[coluna]
r = adfuller(series, autolag='AIC')
output = {'estatística_do_teste': round(r[0], 4), 'valor_p': round(r[1], 4), 'número_de_lags': round(r[2], 4), 'número_de_observações': r[3]}
valor_p = output['valor_p']
def ajustar(valor, comprimento=6):
return str(valor).ljust(comprimento)
# Imprimir resumo
print(f'Teste de Dickey-Fuller Aumentado em "{coluna}"', "\n", '-' * 47)
print(f'Hipótese Nula: Os dados possuem raiz unitária. Não estacionários.')
print(f'Nível de Significância = {signif}')
print(f'Estatística do Teste = {output["estatística_do_teste"]}')
print(f'Número de Lags Escolhidos = {output["número_de_lags"]}')
for chave, valor in r[4].items():
print(f'Valor Crítico {ajustar(chave)} = {round(valor, 3)}')
if valor_p <= signif:
print(f" => Valor-P = {valor_p}. Rejeitando a Hipótese Nula.")
print(f" => A série é Estacionária.")
else:
print(f" => Valor-P = {valor_p}. Evidência fraca para rejeitar a Hipótese Nula.")
print(f" => A série não é Estacionária.")
print("\n")
# Realiza o teste para as séries do df
adfuller_test(dados)
<pre>
Código
Teste de Dickey-Fuller Aumentado em "VIXCLS"
-----------------------------------------------
Hipótese Nula: Os dados possuem raiz unitária. Não estacionários.
Nível de Significância = 0.05
Estatística do Teste = -4.5299
Número de Lags Escolhidos = 9
Valor Crítico 1% = -3.435
Valor Crítico 5% = -2.864
Valor Crítico 10% = -2.568
=> Valor-P = 0.0002. Rejeitando a Hipótese Nula.
=> A série é Estacionária.
Teste de Dickey-Fuller Aumentado em "cambio"
-----------------------------------------------
Hipótese Nula: Os dados possuem raiz unitária. Não estacionários.
Nível de Significância = 0.05
Estatística do Teste = -2.0463
Número de Lags Escolhidos = 1
Valor Crítico 1% = -3.435
Valor Crítico 5% = -2.864
Valor Crítico 10% = -2.568
=> Valor-P = 0.2667. Evidência fraca para rejeitar a Hipótese Nula.
=> A série não é Estacionária.
Teste de Dickey-Fuller Aumentado em "DGS10"
-----------------------------------------------
Hipótese Nula: Os dados possuem raiz unitária. Não estacionários.
Nível de Significância = 0.05
Estatística do Teste = -0.1662
Número de Lags Escolhidos = 0
Valor Crítico 1% = -3.435
Valor Crítico 5% = -2.864
Valor Crítico 10% = -2.568
=> Valor-P = 0.9424. Evidência fraca para rejeitar a Hipótese Nula.
=> A série não é Estacionária.
2) Definir a ordem máxima (m) de integração entre as variáveis.
Como verificado anteriormente, ambas as séries não são estacionárias de acordo com o teste ADF. De forma a simplificar o processos, vamos definir que, como boa parte das séries econômicas, as séries sejam estacionarias a partir de uma simples diferenciação, e portanto, que sejam I(1).
3) Montar o VAR em nível para as variáveis.
# Instância a classe VAR com os dados var = VAR(dados)
4) Determinar a ordem de defasagem do VAR(p) pelos critérios de informação tradicionais
Por meio do método select_order, verificamos que a partir de diferentes critérios de seleção para os dados utilizados, temos p = 2.
A partir disso, ajustamos um VAR(2).
# Verificar a ordem de defasagem do VAR por critérios de seleção order = var.select_order(maxlags = 6, trend = "ct") # Verifica as ordens de acordo com critérios de seleção order.selected_orders
Código
{'aic': 4, 'bic': 2, 'hqic': 2, 'fpe': 4}# Realiza o ajuste do VAR(2) com constante e tendência var_result = var.fit(maxlags = 2, trend = 'ct')
5) Ver a estabilidade do modelo, em particular problemas de autocorrelação
O Portmanteau Test é usado para avaliar se existe autocorrelação residual significativa em um modelo ajustado, ou seja, se há dependência linear entre os resíduos em diferentes defasagens.
Se os resíduos são verdadeiramente aleatórios, espera-se que as autocorrelações sejam próximas de zero. O teste calcula uma estatística de teste baseada nas autocorrelações dos resíduos em várias defasagens e a compara com uma distribuição qui-quadrado para determinar se há autocorrelação significativa.
Queremos achar um modelo tal que não rejeite a hipótese nula de ausência de autocorrelação, isto é, não desejamos obter um resultado do p-value do Portmanteau Test menor de 0,05 (5%).
Rejeitamos a hipótese nula, entretanto, confirmamos a estabilidade do modelo. De forma a finalizar o exercício, ignoraremos esse problema e aplicamos o restante dos processos.
# Realiza o teste de correlação serial dos erros var_auto = var_result.test_whiteness() print(var_auto.summary())
Código
Portmanteau-test for residual autocorrelation. H_0: residual autocorrelation up to lag 10 is zero. Conclusion: reject H_0 at 5% significance level.
========================================
Test statistic Critical value p-value df
----------------------------------------
129.2 92.81 0.000 72
----------------------------------------var_result.is_stable()
True
6) Adicionar m defasagens ao VAR, de modo que você terá um VAR(p+m);
# Realiza o ajuste do VAR(3) com constante e tendência var_result_m = var.fit(maxlags = 3, trend = 'ct')
7) Rodar o teste de Wald com p coeficientes e p graus de liberdade.
Agora vamos verificar a causalidade.
Para tanto, utilizamos o Wald test, que é um teste estatístico utilizado para avaliar a significância dos coeficientes estimados em modelos de regressão. Ele é baseado na comparação entre a estimativa do coeficiente e a sua variância estimada.
Para tanto vamos testar a hipótese nula de que um coeficiente é igual a zero. A ideia é verificar se a estimativa do coeficiente é estatisticamente diferente de zero, o que indicaria a presença de um efeito significativo da variável explicativa correspondente sobre a variável resposta.
Se a estatística de teste calculada for maior do que o valor crítico da distribuição qui-quadrado, rejeita-se a hipótese nula, indicando que o coeficiente é significativamente diferente de zero.
Por outro lado, se a estatística de teste for menor do que o valor crítico, não há evidência suficiente para rejeitar a hipótese nula, sugerindo que o coeficiente não é significativamente diferente de zero.
# Realiza o teste de causalidade de Toda-Yamamoto causality_test1 = var_result_m.test_causality(caused = 'VIXCLS', causing = ['cambio'], kind = 'wald') print(causality_test1.summary())
Código
Granger causality Wald-test. H_0: cambio does not Granger-cause VIXCLS. Conclusion: fail to reject H_0 at 5% significance level.
========================================
Test statistic Critical value p-value df
----------------------------------------
7.629 7.815 0.054 3
----------------------------------------</pre> # Realiza o teste de causalidade de Toda-Yamamoto causality_test2 = var_result_m.test_causality(caused = 'cambio', causing = ['VIXCLS'], kind = 'wald') print(causality_test2.summary()) <pre>
Código
Granger causality Wald-test. H_0: VIXCLS does not Granger-cause cambio. Conclusion: reject H_0 at 5% significance level.
========================================
Test statistic Critical value p-value df
----------------------------------------
16.05 7.815 0.001 3
----------------------------------------Considerações
Considerado o exercício, podemos dizer que o VIX granger causa Câmbio. Ou seja, há precedência temporal do índice sobre o câmbio brasileiro.
Quer aprender mais?
- Cadastre-se gratuitamente aqui no Boletim AM e receba toda terça-feira pela manhã nossa newsletter com um compilado dos nossos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas;
- Quer ter acesso aos códigos, vídeos e scripts de R/Python desse exercício? Vire membro do Clube AM aqui e tenha acesso à nossa Comunidade de Análise de Dados;
- Quer aprender a programar em R ou Python com Cursos Aplicados e diretos ao ponto em Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas? Veja nossos Cursos aqui.