Meirelles e Tombini visitam o R

O Banco Central brasileiro (BCB) tem sido muito criticado ultimamente, especialmente em se tratando de como ele tem respondido às flutuações do PIB e do nível de preços. Até mesmo questionamentos em relação a sua independência têm surgido. Críticos ao posicionamento do BCB têm insinuado que ele está menos rigoroso com o tratamento da inflação e, desta forma, tem tentado alimentar um crescimento artificial da economia.

Neste exercício simples eu tento estimar justamente isto, a resposta do BCB (através da taxa de juros) a choques na inflação e na taxa de desemprego (ou seja, uma proxy do nível de atividade da economia) durante dois períodos de 4 anos cada um. Durante o primeiro período, de 2007 até dezembro de 2010, o BCB foi presidido por Henrique Meirelles enquanto que no segundo período, de 2011 até dezembro de 2014, foi presidido pelo atual presidente do BCB, Alexandre Tombini.

O principal problema que surge aqui é o fato de que as amostras são extremamente pequenas (48 observações cada) para estimarmos um VAR. Note que se escolhermos, por exemplo, 4 defasagens para cada equação teremos que estimar (4*3+1)*3 parâmetros. Isto é, teremos que estimar 39 parâmetros usando 48 observações. Logo, a minha escolha de usar o pacote BMR novamente, onde posso estimar um BVAR usando informações a priori sobre os parâmetros, se faz óbvia.

Abaixo o gráfico com os dados utilizados.

dates <- seq(as.Date('2002-03-01'), as.Date('2014-12-01'), by='1 month')
gtsplot(data, dates=dates)

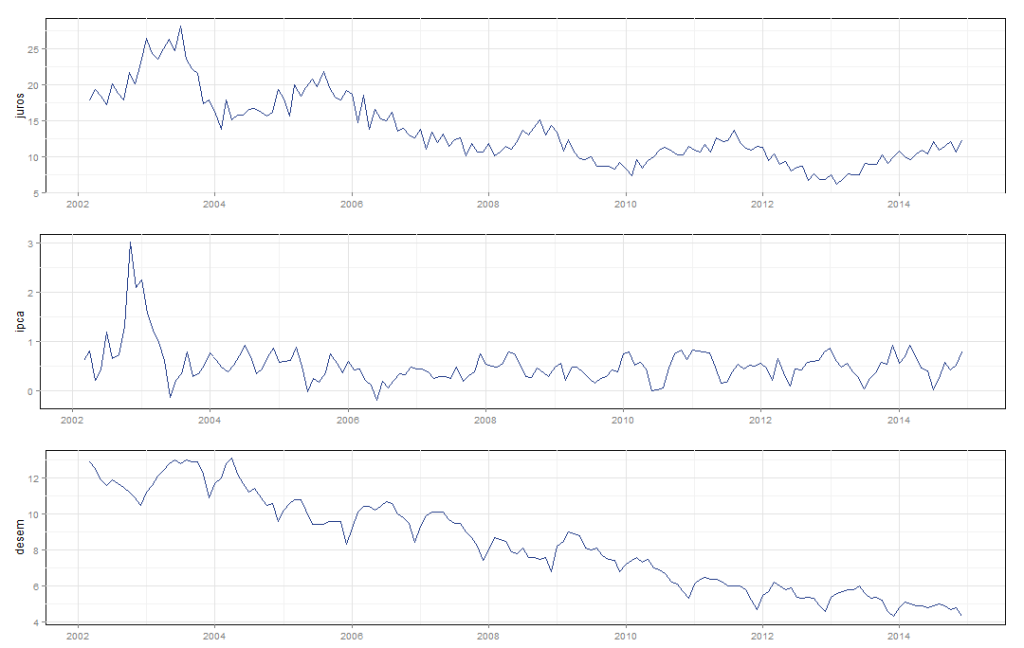
O primeiro passo agora é então tentar inferir sobre os coeficientes AR(1) para usarmos como informação a priori*. Eu decidi não assumir raiz unitária e usei os valores 0.94, 0.73 e 0.97 para as séries de taxa de juros, IPCA e taxa de desemprego, respectivamente. Estes valores foram baseados nas funções parciais de autocorrelação dadas abaixo**.

gpacf(data, save=F)

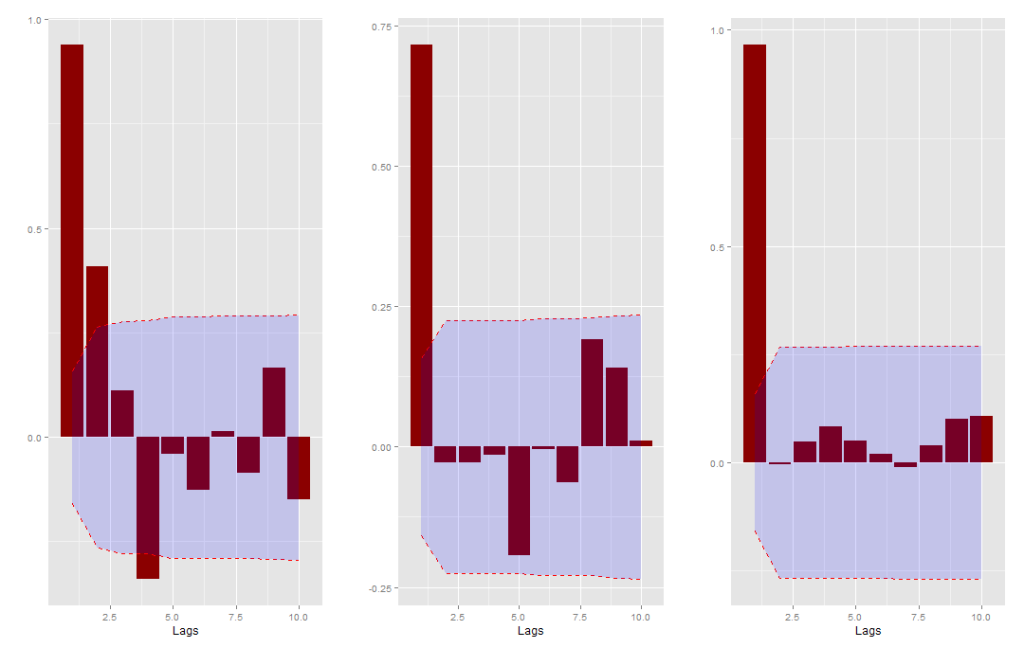
Em seguida podemos estimar o mesmo modelo para os dois períodos distintos.

prior <- c( 0.94,   0.73,    0.97)

bvar.m <- BVARM(meir,coefprior=prior,p=12,constant=TRUE,
                irf.periods=20,keep=10000,burnin=1000,
                VType=1,decay="H",HP1=0.05,HP2=0.5,HP3=1,HP4=2)

bvar.t <- BVARM(tomb,coefprior=prior,p=12,constant=TRUE,
                irf.periods=20,keep=10000,burnin=1000,
                VType=1,decay="H",HP1=0.05,HP2=0.5,HP3=1,HP4=2)

Feito isto, extraímos as séries de impulso resposta e criamos também uma série que acumula estas respostas (assim podemos ver o efeito total do choque). A seguir estão os gráficos que mostram como que a taxa de juros responde a choques nas séries de inflação e na taxa desemprego. Devido ao tamanho do código referente ao gráfico das respostas eu só vou incluir o código referente ao primeiro gráfico.

#### Extraindo IRFs ####

irf.m <- IRF(bvar.m, save=F)
irf.t <- IRF(bvar.t, save=F)

irfs.ipca <- ts(cbind(irf.m$IRFs[1:20,2,1,2],
                      irf.t$IRFs[1:20,2,1,2]))

irfs.desem <- ts(cbind(irf.m$IRFs[1:20,2,1,3],
                       irf.t$IRFs[1:20,2,1,3]))

#### Acumulando os IRFs ####

irfsc.ipca <-  ts(apply(irfs.ipca, 2, cumsum))
irfsc.desem <- ts(apply(irfs.desem, 2, cumsum))

#### Gráficos ####

plot(irfs.ipca[,1],
     xlab='',
     main='Choque no IPCA',
     ylab='SELIC',
     bty='l',
     ylim=c(-0.5,0.8),
     col='darkblue',
     lwd=2)

abline(h=0, col='darkgrey')

lines(irfs.ipca[,2],
      col='darkred',
      lwd=2)

legend('topright',
       lty=1, col=c('darkblue', 'darkred'),
       legend=c('Meirelles', 'Tombini'),
       bty='n', lwd=2)

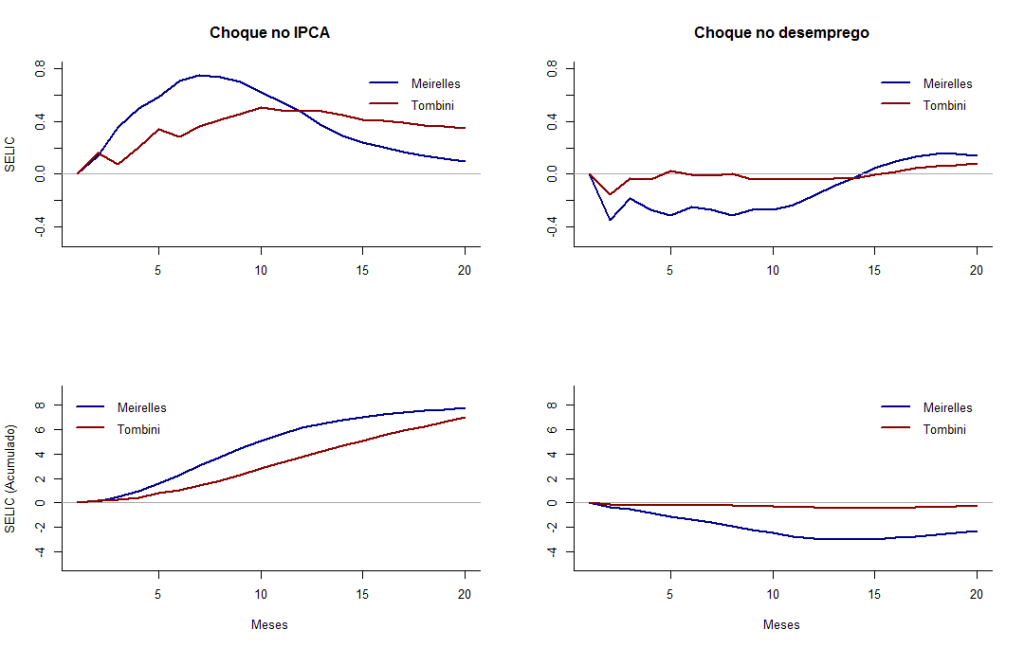
Pelos gráficos acima podemos ver que, a resposta por parte do BCB a choques, seja no IPCA ou na taxa de desemprego, foi bem mais lenta e em níveis menores no período em que foi presidido pelo Alexandre Tombini quando comparado ao período de Henrique Meirelles.

Logo, este simples exercício mostra indícios de que o BCB nos últimos 4 anos não tem sido tão “agressivo” quanto costumava ser nos tempos de Meirelles.

* Utilizando a função stationarity podemos notar que as séries podem apresentar problemas de raiz unitária. Esta informação pode ser usada na estimação, isto é, podemos assumir que as séries seguem um passeio aleatório (colocando o input coefprior da função BVARM igual a NULL. Os resultados, porém, não foram sensíveis a esta mudança.

** Além disso, eu assumo que os coeficientes AR(q>1) são todos iguais a zero.