Vamos investigar a atratividade da meta de inflação em relação às expectativas dos agentes privados no Brasil. Em outras palavras, verificaremos se a meta de inflação definida pelo Conselho Monetário Nacional (CMN) tem sido uma variável importante para explicar o comportamento das expectativas de inflação dos agentes econômicos. Para isso, nos basearemos em Carvalho e Minella (2012) e Bevilaqua, Mesquita e Minella (2008) para construir um modelo explicativo para as expectativas de inflação. A estimação será feita via Mínimos Quadrados Ordinários e Mínimos Quadrados em 2 Estágios (TSLS) com instrumentos. Faremos o uso do Python para realizar a coleta e tratamento dos dados, bem como o ajuste do modelo.
A hipótese de expectativas racionais, elaborada por MUTH (1961), teve grande impacto sobre a teoria de política monetária. Por um lado, influenciou o desenvolvimento de ampla literatura sobre qual seria a melhor forma de conduzir a política monetária: se por meio de regras ou de forma discricionária. Por outro, é responsável tanto pelo comprometimento com metas explícitas para inflação quanto pela maior transparência nas ações de Bancos Centrais ao redor do mundo.
A contribuição seminal de KYDLAND and PRESCOTT (1977) usou a hipótese de expectativas racionais para mostrar que políticas discricionárias são inconsistentes intertemporalmente. Tentar manter a taxa de desemprego abaixo daquela considerada natural gerará apenas mais inflação nos períodos seguintes. BARRO and GORDON (1983a) e BARRO and GORDON (1983b), por seu turno, mostraram que em um ambiente onde existe predisposição inflacionária por parte dos Bancos Centrais e inconsistência intertemporal, a busca por reputação ou credibilidade tem um papel importante no relacionamento entre autoridade monetária e o público.
Uma literatura significativa foi desenvolvida a partir desses dois trabalhos. Nela, buscou-se inferir qual seria a melhor forma de conduzir a política monetária. Enquanto a discrição estava sujeita à inconsistência intertemporal, seguir uma regra muito rígida comprometia a estabilização do produto em um ambiente econômico cercado de incerteza. Dentre as várias formas de enfrentar o trade-off entre comprometimento e flexibilidade, o regime de metas explícitas para inflação tem sido utilizado por diversos países atualmente. Esse regime, em sua abordagem flexível, serve tanto para ancorar as expectativas dos agentes privados como dá a possibilidade do policymaker acomodar ou reagir a choques sobre a estrutura econômica.
Metodologia e Variáveis
Estimamos os determinantes das previsões de inflação seguindo a abordagem em Bevilaqua et al. (2008). A escolha das variáveis a serem incluídas na regressão se baseia na suposição de que o mercado acredita que a dinâmica da inflação seja retratada por uma curva de Phillips básica. Em outras palavras, variáveis que normalmente são encontradas empiricamente ou teoricamente como determinantes da inflação são testadas para explicar o comportamento das expectativas de inflação. Em particular, incluímos o hiato do produto, a inflação passada, a variação da taxa de câmbio e a variação do preço das commodities no conjunto de regressores. A meta de inflação também entra como um regressor, pois espera-se que ele funcione como uma âncora para as expectativas de inflação. A equação estimada é a seguinte:
(1)
onde é a expectativa de inflação para os próximos 12 meses,
é a meta de inflação para os próximos 12 meses,
é a inflação acumulada nos últimos 12 meses,
é a taxa de câmbio R$/US$,
é o índice IC-br e
é o hiato do produto obtido a partir do PIB mensal do IBRE/FGV via Filtro de Hamilton.
Com base na equação, verificaremos se a meta de inflação continua sendo importante para explicar o comportamento das expectativas. Importamos abaixo as variáveis utilizadas para estimar a equação, além da taxa de juros Selic, que será utilizada como instrumento.
Para obter todo o código em R e Python para os exemplos abaixo, faça parte do Clube AM, o repositório de códigos da Análise Macro, contendo exercícios semanais.
Comparação de Modelos
Realizamos uma comparação dos coeficiente estimados de ambos os modelos abaixo:
Código
Model Comparison
==========================================================
OLS 2SLS
----------------------------------------------------------
Dep. Variable ipca_exp_12m ipca_exp_12m
Estimator OLS IV-2SLS
No. Observations 252 252
Cov. Est. kernel kernel
R-squared 0.6617 0.6617
Adj. R-squared 0.6548 0.6548
F-statistic 70.019 68.934
P-value (F-stat) 1.016e-13 1.708e-13
=================== ============== ==============
Intercept 0.2020 0.1111
(0.1815) (0.1008)
meta_lead_12 0.6336 0.6556
(2.7413) (2.8141)
inflacao_shift_1 0.3377 0.3369
(8.0084) (7.6719)
delta_dol_shift_1 1.1527 1.1542
(2.4494) (2.5072)
delta_ic_shift_1 -0.0067 -0.0065
(-1.3123) (-1.2793)
hiato_shift_2 0.0469 0.0474
(2.7599) (2.7978)
===================== ================ ===================
Instruments meta_lead_shift_2
inflacao_shift_1
inflacao_shift_2
delta_dol_shift_1
delta_dol_shift_2
delta_ic_shift_1
hiato_shift_2
selic_shift_1
selic_shift_2
----------------------------------------------------------
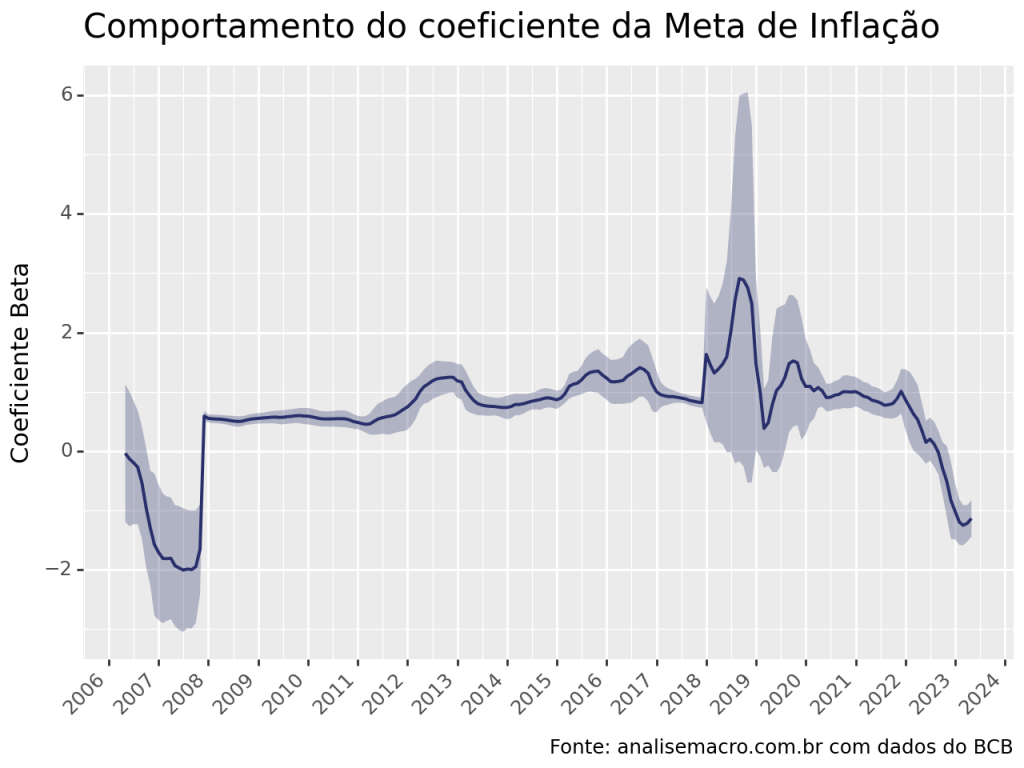
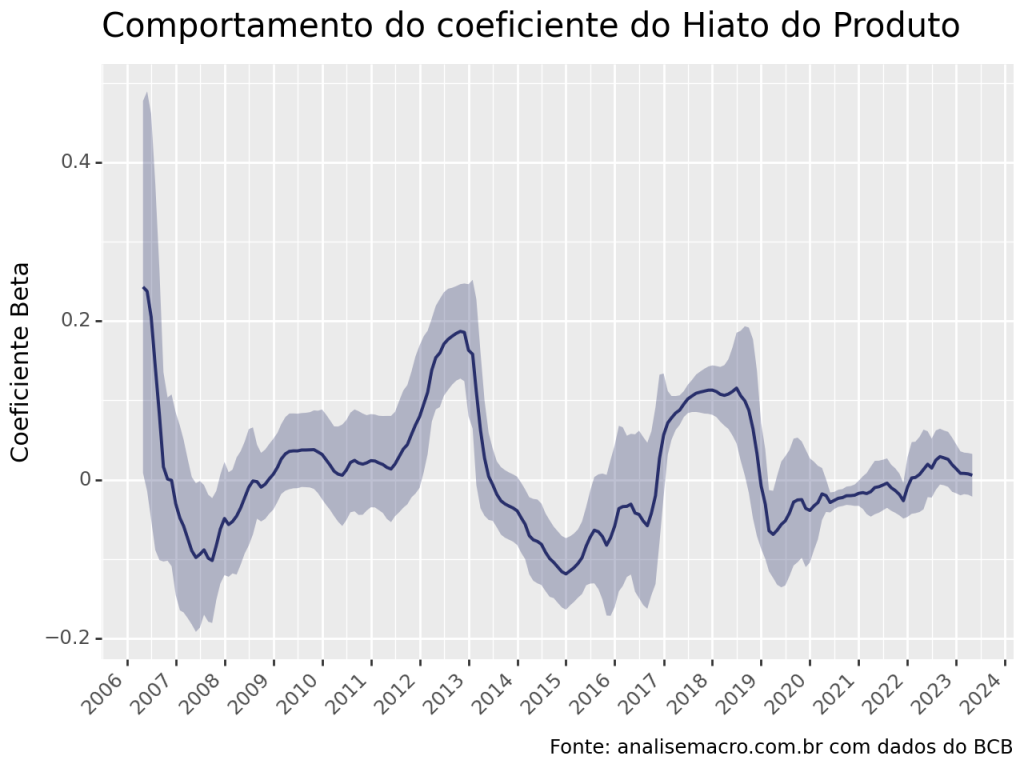
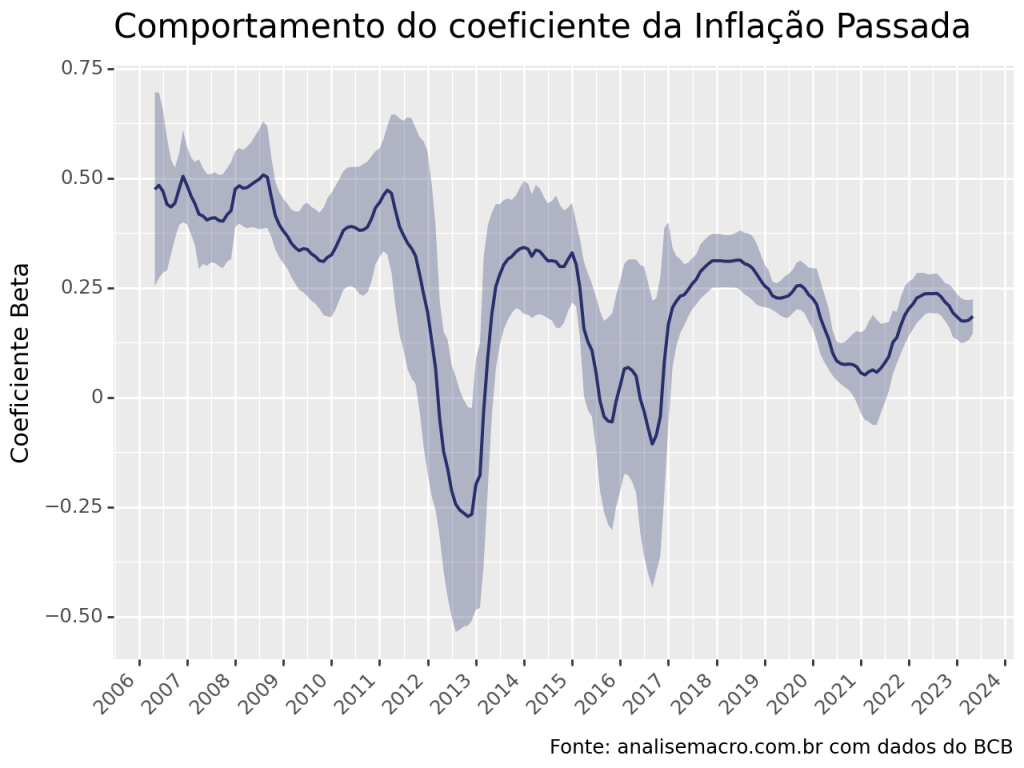
Rolling Regression
De forma a compreender a relação dinâmica entre as variáveis, estimamos uma regressão em janelas deslizantes de 48 meses de forma a obter o coeficiente beta de cada variável. Abaixo, os coeficientes estimado via OLS.
___________________________________
Quer aprender mais?
Seja um aluno da nossa trilha de Macroeconomia Aplicada e aprenda a criar projetos voltados para a Macroeconomia.
Referências
BARRO, R. J., and D. B. GORDON. 1983a. “A Positive Theory of Monetary Policy in a Natural Rate
Model.” The Journal of Political Economy 91 (4): 589–610.
———. 1983b. “Rules, Discretion and Reputation in a Model of Monetary Policy.” Journal of Monetary
Economics 12 (7): 101–21.
Bevilaqua, A. S., M. Mesquita, and A. Minella. 2008. “Brazil: Taming Inflation Expectations.” Bank
for International Settlements (Ed.), Transmission Mechanisms for Monetary Policy in Emerging Market
Economies, no. 35: 139–58.
Carvalho, F. A., and A. Minella. 2012. “Survey Forecasts in Brazil: A Prismatic Assessment of
Epidemiology, Performance and Determinants.” Journal of International Money and Finance 31:
1371–91.
KYDLAND, F. E., and E. C. PRESCOTT. 1977. “Rules Rather Than Discretion: The Inconsistency of
Optimal Plans.” The Journal of Political Economy 85 (3): 473–92.
MUTH, J. F. 1961. “Rational Expectations and the Theory of Price Movements.” Econometrica 29 (3):
315–35.
Pastore, A. C. 2015. Inflação E Crises - O Papel Da Moeda. Editora Campus.