Introdução
Frequentemente, séries temporais podem ser desagregadas em vários atributos de interesse. Por exemplo1, o número total de veículos produzidos no país ao longo do tempo pode ser dividido em veículos comerciais leves, caminhões, ônibus, etc. Cada uma dessas categorias pode ainda ser desagregada em outros níveis, por regiões, por fabricante, etc., caracterizando o que pode ser chamado de "séries temporais hierárquicas".
Essa riqueza de informação e dados possibilita (e pode ser de interesse) gerar previsões desagregadas das séries, de modo que os pontos de previsão das séries desagregadas possam ser analisados individualmente e que, quando agregados de alguma forma, sejam coerentes com os valores agregados da série.
Aprenda a coletar, processar e analisar dados na formação de Do Zero à Análise de Dados Econômicos e Financeiros com Python.
Quer aprender a como criar modelos de previsão? Veja nosso curso Modelagem e Previsão usando Python.
Previsão Hierárquica
Existem várias abordagens para gerar previsões hierárquicas com séries temporais, a mais comum e intuitiva é a bottom-up (de baixo para cima), onde primeiro geramos as previsões para cada série no nível inferior e, em seguida, somamos os pontos de previsão para obter previsões da série acima.
Por outro lado, a abordagem top-down (de cima para baixo) envolve primeiro a geração de previsões para a série agregada e, em seguida, desagregá-la na hierarquia utilizando proporções (geralmente baseadas na série histórica).
Ainda existem outras abordagens como a do Minimum Trace e suas variantes, sendo que cada uma tem seus prós e contras. Para se aprofundar no tema veja Forecasting: principles and practice de Hyndman, R.J., & Athanasopoulos, G. (2021), que apresenta detalhes sobre as abordagens disponíveis.
Exemplo: dados de produção da ANFAVEA
Mensalmente a ANFAVEA disponibiliza séries temporais da produção, licenciamento, exportação, etc. de veículos. Os dados são desagregados pelas categorias citadas acima e neste exemplo iremos explorar alguns métodos de gerar modelos de previsão para as séries de produção de veículos.
Os dados são coletados via SGS do BCB usando a biblioteca python-bcb, no período de jan/1993 até jul/2024. A separação de treino/teste ocorre nos doze últimos meses da série.
Bibliotecas
Para a análise, vamos utilizar as seguintes bibliotecas Python:
-
- python-bcb: Para acessar os dados do SGS.
- hierarchicalforecast: Para realizar previsões hierárquicas.
- statsforecast: Para utilizar modelos de séries temporais.
- pandas: Para manipulação de dados.
- plotnine: Para gerar gráficos.
Coleta dados
O primeiro passo é coletar os dados do SGS. Utilizaremos a função sgs.get() para buscar as séries temporais de produção de veículos, desde janeiro de 1993 até julho de 2024.
Tratamento de Dados
Após coletar os dados, devemos transformá-los em um formato adequado para a análise. Isso inclui:
- Limpar e padronizar os nomes das colunas.
- Converter a coluna de data para o formato
datetime. - Criar uma coluna 'top_level' com o valor 'Total' para indicar o nível superior da hierarquia.
- Transformar o DataFrame para o formato 'long', separando as categorias de veículos em diferentes linhas.
Criação do Modelo
Para realizar as previsões, vamos utilizar o objeto StatsForecast. Esse objeto permite utilizar diferentes modelos de séries temporais, como AutoARIMA, AutoETS e Naive.
Após gerar as previsões com os diferentes modelos, precisamos reconciliá-las para garantir a coerência entre os níveis da hierarquia. Para isso, vamos utilizar o objeto HierarchicalReconciliation.
Após a reconciliação das previsões, precisamos avaliá-las. Para isso, vamos utilizar o objeto HierarchicalEvaluation. O objetivo é comparar as previsões com os dados reais do conjunto de teste e calcular o erro quadrático médio (MSE).
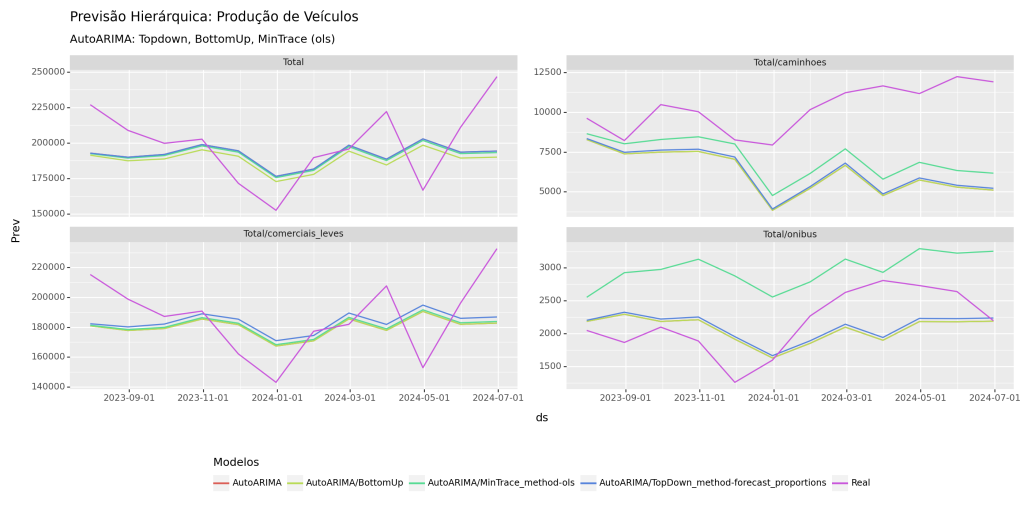
Podemos também avaliar as previsões visualmente, comparando os dados de previsão com os dados de teste.
Conclusões
A modelagem preditiva de séries temporais hierárquicas é uma ferramenta poderosa para analisar e prever dados que se estruturam em diferentes níveis de granularidade. Com a utilização das bibliotecas Python e dos métodos descritos neste artigo, você pode aplicar essa técnica para obter insights e tomar decisões mais precisas em seus projetos.
Quer aprender mais?
Clique aqui para fazer seu cadastro no Boletim AM e baixar o código que produziu este exercício, além de receber novos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas diretamente em seu e-mail.