O termo "Machine Learning" foi cunhado por Arthur Samuel em 1959 e definido como a capacidade que proporciona aos computadores a habilidade de aprender sem requerer programação explícita. Ao longo do tempo, essa área tem evoluído em paralelo com os avanços computacionais, consolidando-se como um elemento crucial na construção de modelos preditivos. Com a profusão de dados, particularmente os de natureza econômica, tornou-se possível a elaboração de modelos de previsão para variáveis macroeconômicas. Este artigo oferece uma introdução a esses tipos de modelos e apresenta um exemplo concreto: a construção de uma previsão para a probabilidade de recessão nos EUA, utilizando as linguagens R e Python.
Para obter todo o código em R e Python para os exemplos abaixo, faça parte do Clube AM, o repositório de códigos da Análise Macro, contendo exercícios semanais.
Machine Learning
O termo “Machine Learning” foi criado por Arthur Samuel em 1959 e definido como “a capacidade que dá aos computadores a capacidade de aprender sem serem programados explicitamente”. Entretanto, apenas no final dos anos 90 os modelos desse arcabouço começaram a se tornar populares. Para a previsão de séries temporais, é possível dizer que o cenário é ainda mais incipiente. Ainda não há um consenso se esses métodos conseguem performar melhor do que os métodos ditos “clássicos” da área. Entretanto, o seu uso ganha cada vez mais adeptos, principalmente quando estamos tratando de bases de dados grandes (Cerqueira, Torgo, e Soares 2019).
Por que ML?
Breiman et al. (2001) argumentam que a comunidade estatística se dividiu em duas culturas:
- Os estatísticos assumem um processo de geração de dados e tentam aprender sobre ele usando dados.
- Os cientistas da computação tratam o mecanismo de dados como desconhecido e tentam prever ou classificar com a maior precisão.
Breiman afirma que a comunidade estatística se concentrou quase que exclusivamente no primeiro, com a interpretação dos parâmetros como questão central dos problemas. Segundo ele: “Esse compromisso levou a uma teoria irrelevante, conclusões questionáveis e impediu que os estatísticos trabalhassem em uma ampla gama de problemas atuais interessantes.”
Muitos dos modelos de machine learning já existiam antes do século XXI. Entretanto, foi com o aumento da capacidade computacional que eles se tornaram populares. Isto se deve a habilidade desses modelos em performar bem quando se é utilizado um grande volume de dados. Além disso, os problemas atuais da área requerem mais esforço na acurácia do que na explicação 1.
Aprendizagem não supervisionada
O aprendizado não supervisionado inclui um conjunto de ferramentas estatísticas que visa compreender e descrever os dados, mas sem a presença de uma variável dependente. Generalizando, o aprendizado não supervisionado tem como objetivo a identificação de grupos em um conjunto de dados baseado em características semelhantes. Esse tipo de aplicação pode servir tanto para identificar grupos de variáveis, o que pode ser útil para casos em que desejamos reduzir a dimensionalidade dos dados, quanto para encontrar grupos nas observações ou indivíduos, os chamados clusters.
Entre os exemplos de usos para esse tipo de abordagem estão: Sistemas de recomendação com base na segmentação de clientes e produtos com comportamentos parecidos, reconhecimento por imagem e detecção de anomalias, como fraudes.
Digamos que nosso objetivo seja separar os países em três grupos com base em duas variáveis, o Índice de Gini e o PIB per capita. Para isso, utilizamos o método de K-means, que divide o conjunto de dados em K grupos diferentes, de acordo com a distância entre os pontos dos mesmos grupos, de modo a minimiza-las.
Aprendizagem supervisionada
Os modelos de aprendizagem supervisionada são aqueles que são usados para tarefas que envolvem a previsão de uma determinada variável de interesse. Os modelos supervisionados tentam descobrir e modelar os relacionamentos entre a variável que está sendo prevista e as variáveis preditoras. Ou seja, utilizando t para prever t+1. Entretanto, esses modelos podem ser divididos em dois tipos: regressão e classificação.
Regressão
Quando o objetivo de nosso aprendizado supervisionado é prever um resultado numérico contínuo, então estamos diante de um problema de regressão. Como um modelo preditivo de regressão prevê uma quantidade, a qualidade do modelo deve ser relatada como um erro nessas previsões.
Classificação
Já os modelos de classificação trabalham com problemas que têm como variável de interesse um dado discreto ou categórico. Ou seja, quando a variável está dividida em “classes”. O número de classes pode variar, mas na maioria dos casos a resposta é binária. Um exemplo de modelo de classificação binária é a regressão logística, que é bastante utilizado pelos economistas. Dentre várias possibilidades de uso desses modelos, alguns exemplos são:
- Previsão da probabilidade de recessão
- Análise de sentimentos em textos
- Identificação de doenças por imagem
- Classificação de um email em “spam” ou “não spam”
Viés x Variância
Antes de definirmos o tradeoff entre viés e variância, é necessário definir individualmente esses dois conceitos.
- Viés - é a diferença entre a previsão média do nosso modelo e o valor correto que estamos tentando prever. O modelo muito viés presta pouca atenção aos dados de treinamento e simplifica demais o modelo, o que leva a um alto erro nos dados de treinamento e teste.
- Variância - é a variabilidade da previsão do modelo para um determinado ponto. O modelo com alta variância dá muita atenção aos dados de treinamento, o que leva a uma generalização ruim sobre os dados que nunca viu. Assim, esses modelos funcionam muito bem em dados de treinamento, mas apresentam altas taxas de erros em dados de teste.
Assim, supondo uma função de perda quadrática, ou seja,
e um processo de geração dos dados
:
Ou seja, o erro pode ser dividido em duas partes, erro redutível e erro irredutível. O primeiro é composto por uma soma do viés e da variância. Resumidamente, o motivo de haver um tradeoff é a capacidade de flexibilização/complexidade do modelo. Um modelo mais inflexível, ou seja, com maior variância terá menor viés e vice-versa. Ou seja, o tradeoff é inevitável. Por isso, é necessário o ajuste no modelo a fim de minimizar viés e variância para níveis adequados. Já a segunda parte, o erro irredutível, como o nome diz não pode ser evitado. Nele estão ruídos inerentes dos dados utilizados.
Overfitting e Underfitting
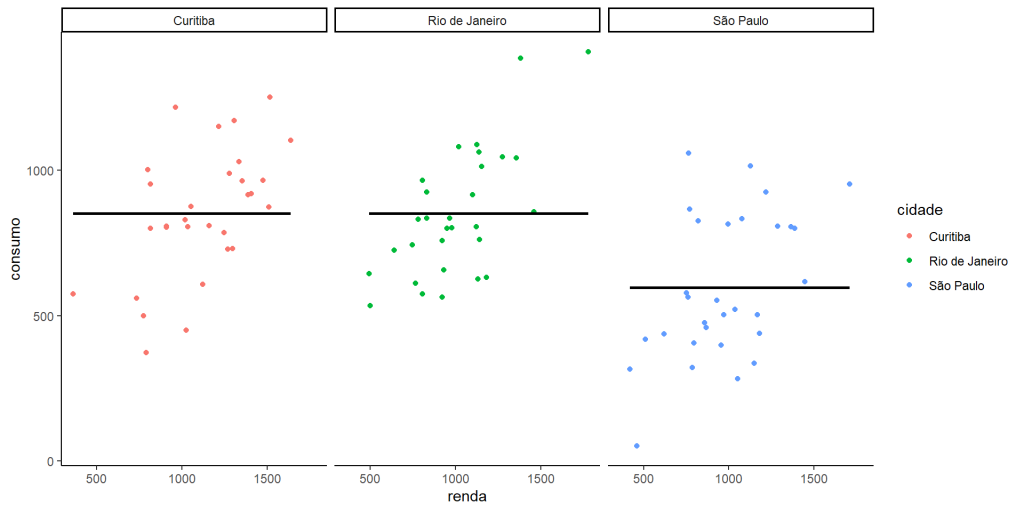
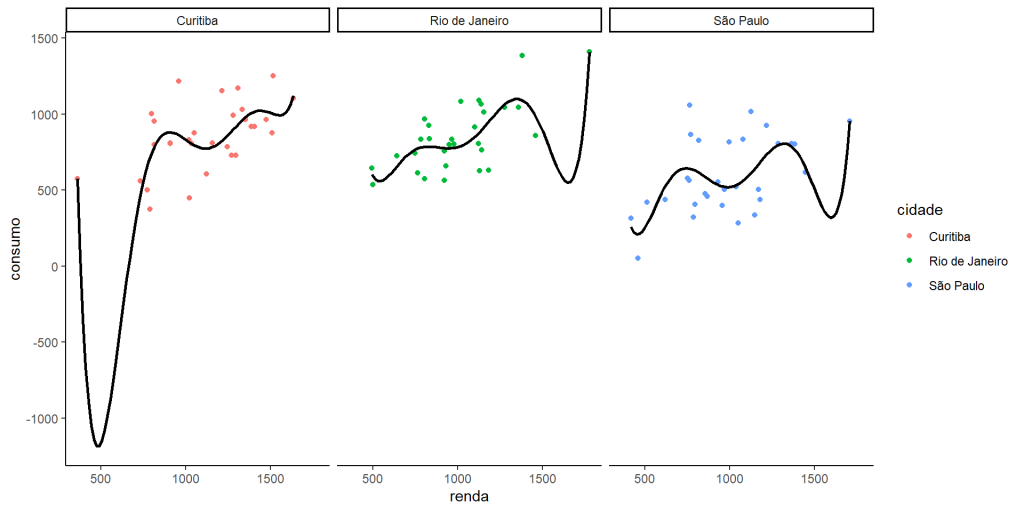
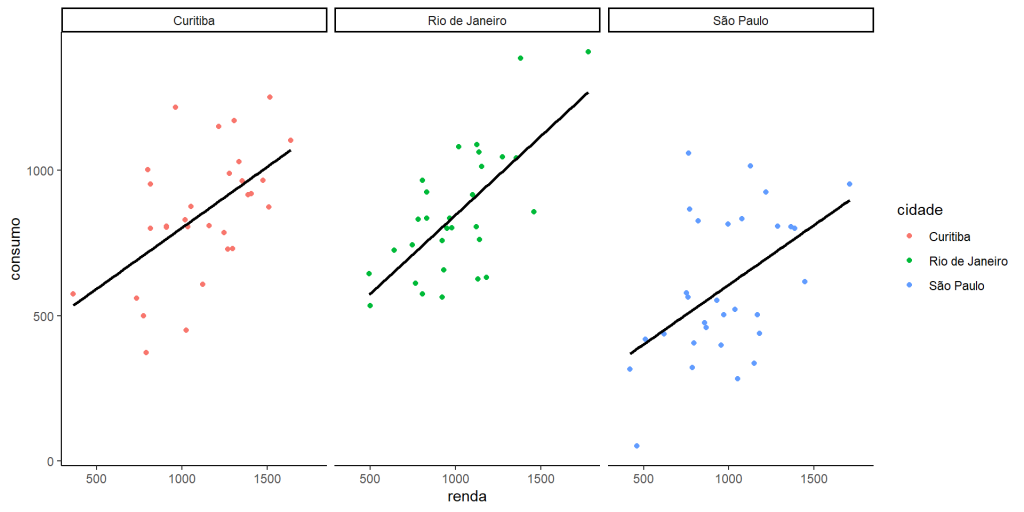
Assim, quando um modelo performa bem nos dados de treino mas não consegue generalizar sua previsões para dados novos, dizemos que há overfitting (alta variância e baixo viés). Isso acontece devido ao modelo capturar o ruído dos dados como informação. O caso contrário (baixa variância e alto viés) é chamado de Overfitting . Neste caso, o modelo deixa de capturar as informações importantes dos dados. Para mostrar esses padrões, fizemos um pequeno exercício de comparação renda e consumo em três diferentes cidades:
Underfitting - Usando apenas a média do consumo estamos no caso extremo, em que não consideração nenhuma pela renda, ou seja .
Overfitting - Se utilizarmos um polinomial de grau 6, impondo mais parâmetros (complexidade) ao modelo, ele fica suscetível demais ao padrão dos dados, especialmente aos outliers.
Modelo adequado - Perceba aqui que nós sabemos que o processo gerador dos dados é linear. Em casos reais isso raramente é verdade.
Soluções
Portanto, o trade-off entre viés e variância nos impõem uma restrição importante. A principio, nós gostaríamos de utilizar todos os dados disponíveis para encontrar todas as relações e não-linearidades possíveis. Entretanto, como vimos, maior complexidade pode levar ao overfit do modelo. Existem algumas soluções para isso:
- K-fold Cross-validation ou validação cruzada - Essa é uma das alternativas mais comuns e necessárias. A ideia é simples. Você separa o seus dados de treino aleatoriamente em
(normalmente 5) partes. Assim, treinamos iterativamente o modelo k vezes utilizando todos as partes menos uma em cada vez. Após isso, é retornado o valor médio da performance desse modelo. Além disso, é possível estimar os hiper parâmetros dos modelos com base nessa validação. Quando estamos tratando de séries temporais, é necessário fazer ajustes nessa abordagem.
- Remover parâmetros - Nem sempre é desejado, mas é possível remover variáveis explicativas da estimação. Alguns modelos já tem alguma funcionalidade nesse sentido como característica, caso do Lasso, por exemplo.
- Ensemble - São técnicas que combinam previsões de múltiplos modelos.
- Utilizar mais dados - Muitas vezes aumentar a amostra pode fazer com que diminua o problema de overfitting. Entretanto, nem sempre isso é possível.
Modelos de ML para previsão
Veremos alguns modelos de machine learning que podem ser utilizados para a previsão de séries temporais.
KNN
K-nearest neighbor (KNN) é um modelo simples, no qual a previsão de cada observação é feita com base em sua proximidade com outras observações. Este método identifica as observações que são mais próximas da observação que está sendo prevista e usa o valor médio da variável de interessa dessas
observações como a previsão.
Por exemplo, digamos que precisamos estimar o preço de um imóvel tendo apenas a localização dele como base. Poderíamos utilizar a longitude e latitude para encontrar o imóveis mais próximos e com isso retornar a média do valor destes. Na prática, independente dos dados utilizados, a lógica permanece. A similaridade será calculada com base na distância entre as observações com base nos parâmetros selecionados.
Lasso
Lasso (Least Absolute Shrinkage and Selection Operator) é um método desenvolvido por Tibshirani (1996) que tem como objetivo reduzir o número de parâmetros, principalmente em casos de multicolineariedade. Assim, é adicionado a minimização dos mínimos quadrados uma penalização baseada na magnitude absoluta dos coeficientes:
Fica evidente com base na equação acima que o valor de é extremamente relevante para o resultado do modelo. Se esse parâmetro aumenta, o viés do estimador também aumenta. Já se ele diminui, quem aumenta é a variância. Caso ele seja 0, ele se torna igual ao estimador OLS. A forma usual de encontrar o valor ótimo de
é por meio da validação cruzada (CV).
Árvores de decisão e Random forest
As árvores de decisão funcionam com base em respostas a perguntas sequenciais que nos enviam para uma determinada rota da árvore dada a resposta. O modelo se comporta com condições “se isso, então”, em última análise, produzindo um resultado específico.
Digamos que é preciso estimar uma previsão para decidir se os clientes de uma instituição financeira podem ter um empréstimo com pequeno ou grande com base em 2 variáveis: histórico e renda. A árvore de decisão estimada com base nos dados internos do banco divide em duas perguntas sequenciais: 1) O cliente tem bom histórico?; 2)O cliente tem boa renda. Nesse exemplo, um potencial resultado é de que clientes com bom histórico podem pegar qualquer tipo de empréstimo, com exceção aqueles de baixa renda, que só podem pegar o empréstimo menor. Já clientes com histórico ruim não podem pegar nenhum tipo, com exceção ao cliente de alta renda, que pode pegar o empréstimo menor.
Entretanto, esse tipo de modelo tende a gerar overfitting. A solução dada pra isso é utilizar técnicas de reamostragem e unir centenas dessas árvores e uma só estimação. São as chamadas Random forests.
Redes neurais
Redes Neurais são um tipo de modelo de machine learning que visa imitar o padrão de aprendizado de redes neurais biológicas. As redes neurais biológicas têm neurônios interconectados que recebem entradas e, com base nessas entradas, produzem um sinal de saída para outro neurônio. Da mesma forma, nos modelos de redes neurais, são criadas varios neurônios e redes que recebem o dado inicial e transformam de alguma forma esse dado para servir de insumo para a rede seguinte. Normalmente esses modelos precisam de uma grande quantidade de dados para conseguir uma performance boa.
Para séries temporais o modelo mais amplamente utilizado é o Recurrent Neural Networks (RNN). O formato é muito semelhante á rede neural padrão. Os neurônios são divididos em camadas de entrada (input), escondidas (hiddens) e saída (output). As camadas escondidas são as camadas entre a entrada e a saída. São nelas em que transformações não-lineares são aplicadas nos dados. A diferença do RNN pra rede neural padrão é que os neurônios nas camadas escondidas são conectados de forma dependente ao tempo. Ou seja, os neurônios do tempo estão conectados aos do neurônios do tempo
e assim por diante.
Exemplo: prevendo a recessão dos EUA.
Para mostrar um exemplo do uso de machine learning para previsão macroeconmétrica, decidimos criar um modelo para previsão de recessão nos Estados Unidos. Para isso, estamos utilizando as seguintes variáveis: taxa de juros do tesouro americano de curto (3 meses) e longo (10 anos) prazo, empregados (excluindo agrícolas) e inflação. Além disso é incluída uma variável de diferença entre a taxa de longo e a de curto prazo, para determinar o ângulo da curva de juros. Para todas as variáveis explicativas são incluídos os lags de 3,6,9 e 12 meses. Nossa variável de interesse é o indicador de recessão mensal produzido pelo NBER adiantado 12 meses. Ou seja, nosso interesse é prever se vai haver uma recessão nos 12 meses subsequentes.
Utilizaremos uma variação do cross validation que ao invés de ordenar os dados aleatóriamente, ordena sequencialmente no tempo.
Utilizaremos os seguintes modelos: Lasso (Regressão Logística com penalização), Random forest e KNN. Todos estão sendo aplicados com o uso do pacote {caret} no R e scikit-learn no Python, que possibilitam um uso uniforme de centenas de algoritmos de machine learning.
Abaixo, temos o resultado das previsões de cada modelo no período de 2006 até
___________________________________
Quer aprender mais?
Seja um aluno da nossa formação em Macroeconomia Aplicada e aprenda a criar projetos voltados para a Macroeconomia.



![Rendered by QuickLaTeX.com \[\begin{aligned} \mathbb{E}\left[\mathrm{SE}\right] &=\mathbb{E}\left[\left(y-\hat{f}\left(x\right)\right)^{2}\right] \\ &=\underbrace{\left(\mathbb{E}\left(\hat{f}\left(x\right)\right)-f\left(x\right)\right)^{2}}_{\text {viés }^{2}}+\underbrace{\mathbb{E}\left[\hat{f}\left(x\right)-\mathbb{E}\left(\hat{f}\left(x\right)\right)\right]^{2}}_{\text {variância }}+\underbrace{\mathbb{E}\left[y-f\left(x\right)\right]^{2}}_{\text {erro irredutível }} \\ &=\underbrace{\operatorname{vies}^{2}+\mathbb{V}\left[\hat{f}\left(x\right)\right]}_{\text {erro redutível }}+\sigma_{\epsilon}^{2} \end{aligned}\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-6122f58ceadc699d47897f7bc62a6d05_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{i=1}^{n}\left(y_{i}-\sum_{j} x_{i j} \beta_{j}\right)^{2}+\lambda \sum_{j=1}^{p}\left|\beta_{j}\right|\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-cffbf4220d4b2e3a4a560c435f4087a2_l3.png)
