Introdução
Este exercício explora a dinâmica da política monetária brasileira através de um modelo de Markov Switching no Python. O objetivo é identificar diferentes regimes de política monetária e como eles influenciam a taxa Selic, a meta de inflação e o hiato do produto.
Para obter o código e o tutorial deste exercício faça parte do Clube AM e receba toda semana os códigos em R/Python, vídeos, tutoriais e suporte completo para dúvidas.
O que é Markov Switching Regression Models
Modelos de Markov Switching Regression (MSDR) são ferramentas estatísticas que permitem analisar séries temporais com mudanças abruptas no comportamento. Esses modelos assumem que a série temporal é gerada por um processo que muda entre diferentes regimes, e que a probabilidade de transição entre esses regimes é governada por uma cadeia de Markov.
Uma cadeia de Markov é um processo estocástico que descreve a evolução de um sistema ao longo do tempo. Em uma cadeia de Markov, o estado futuro do sistema depende apenas do estado atual, e não de estados anteriores.
Em modelos de Markov Switching, a mudança de regime é modelada por uma cadeia de Markov. Isso significa que a probabilidade de transição para um determinado regime depende apenas do regime atual, e não de regimes anteriores.
Dados Utilizados no Exercício
Vamos nos basear em uma Regra de Taylor Forward-looking. Os dados utilizados neste exercício incluem:
- Taxa Selic: A taxa de juros básica da economia brasileira, definida pelo Comitê de Política Monetária (Copom) do Banco Central do Brasil.
- Meta de Inflação: A meta de inflação definida pelo Conselho Monetário Nacional (CMN).
- Expectativa de Inflação: A expectativa de inflação do mercado para o IPCA, medida pela pesquisa Focus do Banco Central do Brasil.
- Hiato do Produto: A diferença entre o produto potencial e o produto real da economia brasileira, medida pelo IFI.
A periodiciodade dos dados são trimestrais em compreendem o período de 2001Q3 até 2024Q4.
Modelo Markov Switching
O modelo utilizado neste exercício é um modelo de Markov Switching Regression com mudança de intercepto. O modelo assume que a taxa Selic é influenciada por três variáveis:
- Taxa Selic defasada em um trimestre: Reflete a inércia da política monetária.
- Desvio da expectativa de inflação em relação à meta: Reflete a resposta da política monetária à inflação.
- Hiato do produto: Reflete a resposta da política monetária ao ciclo econômico.
Esse modelo também assume que a taxa Selic é influenciada por dois regimes de política monetária:
- Regime 0: Um regime de política monetária restritiva, com um intercepto positivo e uma forte dependência da taxa Selic defasada.
- Regime 1: Um regime de política monetária mais expansiva, com um intercepto negativo e uma menor dependência da taxa Selic defasada.
Estimamos por máxima verossimilhança, e os resultados são utilizados para analisar a dinâmica da política monetária brasileira.
Regra de Taylor com Markov Switching
O exemplo modela a taxa Selic como ruído em torno de um intercepto constante, mas onde o intercepto muda durante diferentes regimes. Também é adicionado variáveis independentes, conforme uma Regra de Taylor Forward-looking: Taxa Selic defasada em 1 trimestre, desvio da expetativa de inflação 4 trimestres à frente em relação a meta e o Hiato do Produto.
![\[r_t = \mu_{S_t} + r_{t-1} \beta_{S_t} + (\Pi^e_{t,t+4} - \Pi_{meta_{t+4}}) \beta_{S_t} + h_{t} \beta_{S_t} + \varepsilon_t \qquad \varepsilon_t \sim N(0, \sigma^2)\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-168db8f81f8217d43709c2fd4628ac4a_l3.png "Rendered by QuickLaTeX.com")
onde 
e as transições dos regimes são
![\[\begin{split} P(S_t = s_t | S_{t-1} = s_{t-1}) = \begin{bmatrix} p_{00} & p_{10} \\ 1 - p_{00} & 1 - p_{10} \end{bmatrix}\end{split}\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-82d5839999041b7b06cf2fb26ba7f4d1_l3.png "Rendered by QuickLaTeX.com")
Estimaremos os parâmetros deste modelo por máxima verossimilhança.
Código
Markov Switching Model Results
==============================================================================
Dep. Variable: Selic No. Observations: 93
Model: MarkovRegression Log Likelihood -150.784
Date: Tue, 01 Apr 2025 AIC 323.569
Time: 09:13:36 BIC 351.427
Sample: 10-01-2001 HQIC 334.817
- 10-01-2024
Covariance Type: approx
Regime 0 parameters
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 4.3317 1.100 3.937 0.000 2.175 6.488
x1 0.6490 0.076 8.593 0.000 0.501 0.797
x2 0.0762 0.871 0.088 0.930 -1.631 1.783
x3 0.0047 0.284 0.017 0.987 -0.553 0.562
Regime 1 parameters
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const -0.2899 0.424 -0.683 0.494 -1.121 0.542
x1 1.0364 0.035 29.865 0.000 0.968 1.104
x2 0.2240 0.326 0.687 0.492 -0.415 0.863
x3 0.1842 0.073 2.514 0.012 0.041 0.328
Non-switching parameters
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
sigma2 1.2207 0.194 6.297 0.000 0.841 1.601
Regime transition parameters
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
p[0->0] 0.7776 0.169 4.609 0.000 0.447 1.108
p[1->0] 0.0624 0.044 1.415 0.157 -0.024 0.149
==============================================================================
Warnings:
[1] Covariance matrix calculated using numerical (complex-step) differentiation.Regimes Identificados
- Regime 0: Caracterizado por uma constante positiva (4.33) e um coeficiente significativo da defasagem da Selic (0.649, p < 0.01), indicando persistência na taxa de juros. As outras variáveis não são estatisticamente significativas.
- Regime 1: A constante negativa (-0.29) sugere um patamar menor de juros, mas não é estatisticamente significativa. A defasagem da Selic tem coeficiente alto (1.036, p < 0.01), indicando forte dependência da Selic anterior. O hiato do produto tem impacto positivo e significativo (0.184, p = 0.012).
Transições Entre Regimes
- p(0→0) = 0.7776 → Probabilidade de permanecer no regime 0 é alta.
- p(1→0) = 0.0624 → Baixa chance de transição do regime 1 para o regime 0.
Interpretação Econômica
- Regime 0 pode estar associado a períodos de juros altos e persistência da política monetária.
- Regime 1 sugere um ciclo mais instável, onde o hiato do produto influencia a taxa Selic.
- O impacto do desvio das expectativas de inflação não foi significativo em nenhum regime.
Plotamos as probabilidades filtradas e suavizadas da política monetária restritiva. Filtrada refere-se a uma estimativa da probabilidade no tempo 
com base nos dados até e incluindo o tempo (mas excluindo os tempos 
). Suavizada refere-se a uma estimativa da probabilidade no tempo usando todos os dados da amostra.
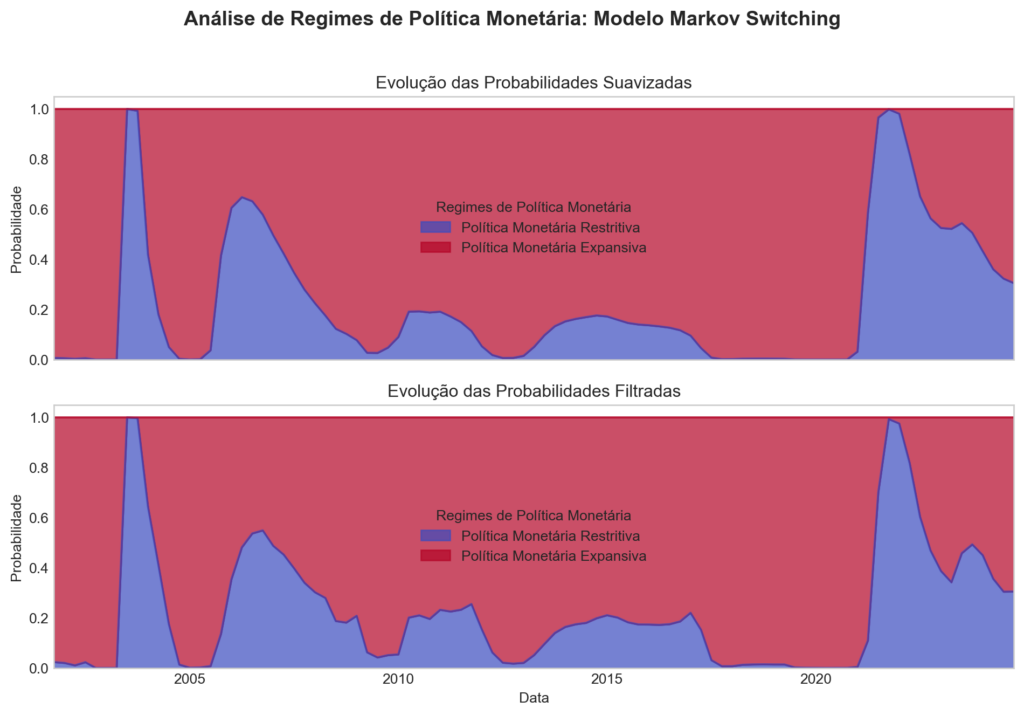
Considerações
O modelo é útil para compreender os diferentes regimes da política monetária brasileira. No entanto, os resultados obtidos não foram suficientes para confirmar a explicação das variáveis selecionadas. As probabilidades geradas, quando comparadas com os padrões aceitos em modelos tradicionais, não sustentaram a necessidade de uma política monetária expansiva durante os períodos de alta inflação, sugerindo o contrário. Isso indica a necessidade de explorar novas especificações e abordagens para aprimorar os resultados.
Quer aprender mais?
Conheça nossa Formação do Zero à Análise de Dados Econômicos e Financeiros usando Python e Inteligência Artificial. Aprenda do ZERO a coletar, tratar, construir modelos e apresentar dados econômicos e financeiros com o uso de Python e IA.
Referência:
Statsmodels. (n.d.). Markov Switching Regression Example. Recuperado de https://www.statsmodels.org/dev/examples/notebooks/generated/markov_regression.html
