Neste artigo verificamos como é possível realizar previsão de variáveis macroeconômicas utilizando os Vetores Autoregressivos.
Modelos multivariados estacionários
Processos autorregressivos de média móvel (ARMA) podem ser facilmente estendidos para o caso multivariado, onde o processo estocástico que gera um vetor de séries temporais é modelado
O mais comum dentre eles é o vetor autorregressivo (VAR), isto porque pode ser facilmente estimado via mínimos quadrados ordinários ou método bayesiano, as suas propriedades têm sido extensivamente estudadas na literatura e também porque são bastante similares às regressões lineares múltiplas.
Um VAR irá descrever a evolução dinâmica de um determinado número de variáveis de acordo com a história comum entre elas. Para ilustrar, considere um vetor autorregressivo de ordem 1, como
(1)
onde e
são ruídos brancos independentes das **estórias** de
e
, mas que podem estar correlacionados.
Se, por exemplo, , significa dizer que a **estória** de
ajuda a explicar
. O sistema acima, a propósito, pode ser representando da seguinte forma, como faz @tsay:
(2)
Ou, ainda, como
Esse sistema de ordem 1, a propósito, pode ser generalizado para qualquer ordem como
{#eq-varp}
onde para
é uma vetor
contendo observações de
séries temporais,
é um vetor
de interceptos,
é uma matriz
de coeficientes e
é um vetor
de erros, independentes e identicamente distribuídos, com média zero e covariância igual a
.
É conveniente representar o VAR com a utilização do operador defasagem como
(3)
Estimação de um VAR
Para obter todo o código em R e Python para os exemplos abaixo, faça parte do Clube AM, o repositório de códigos da Análise Macro, contendo exercícios semanais.
Para ilustrar, vamos considerar um exemplo envolvendo algumas variáveis bastante conhecidas:
- inflação mensal medida pelo IPCA;
- expectativas em t para t+1 para a taxa de inflação mensal;
- IC-br;
- taxa de câmbio R
;
- taxa Selic anualizada;
- taxa de desemprego medida pela PNAD Contínua.
- IBC-br
Os dados são importados abaixo.
Código
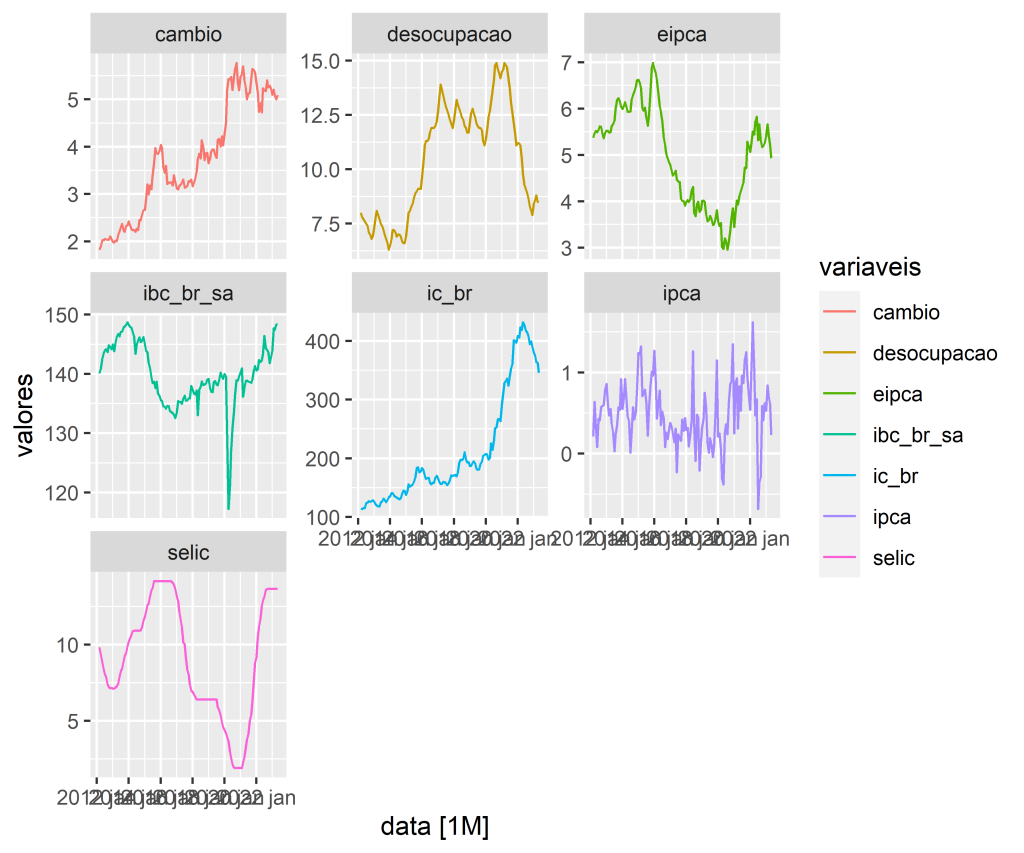
Um ponto importante que devemos nos atentar, para garantir a estabilidade do modelo, é a estacionariedade das séries. O gráfico abaixo deixa isso mais claro.
Acaso o leitor aplique o Teste ADF Sequencial visto na seção anterior, verá que algumas de nossas séries não são estacionárias. Isso, como vimos, pode ser um problema para a estabilidade do nosso VAR.
Código
ipca desocupacao eipca cambio selic ic_br
0 1 1 1 2 1
ibc_br_sa
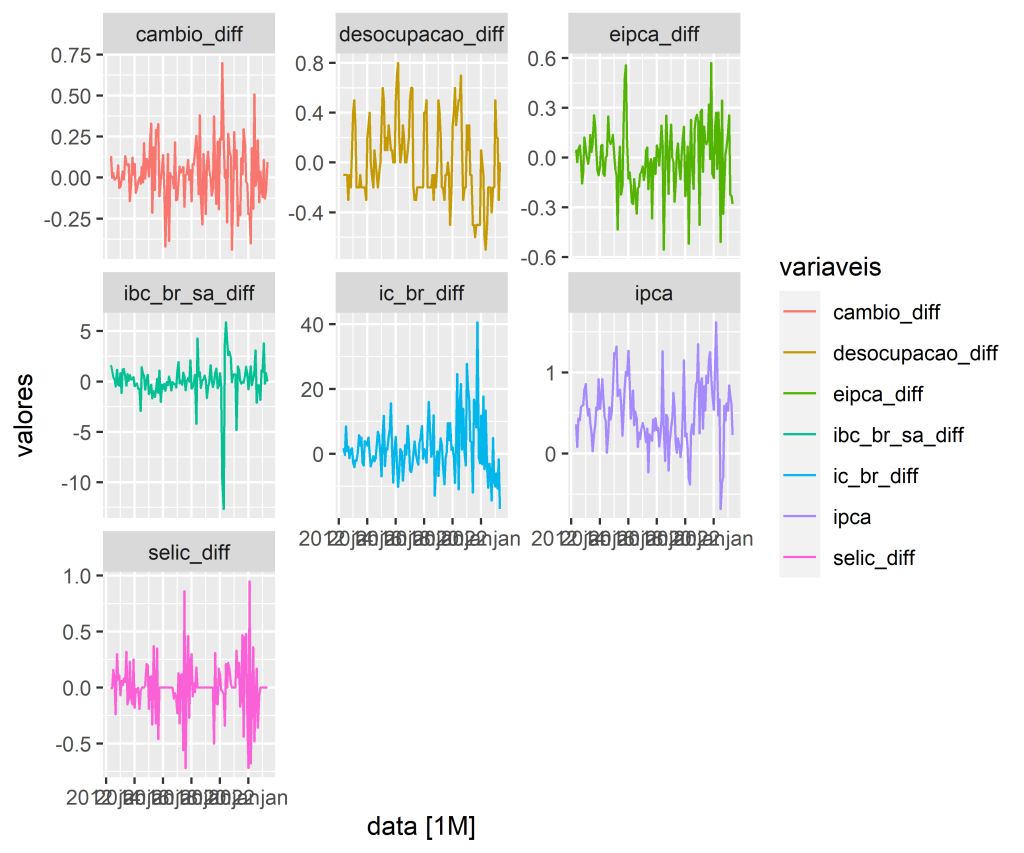
1 Assim, de modo a contornar o problema, vamos simplesmente diferenciar as séries que consideramos não estacionárias. Vejamos agora o resultado visual das séries diferenciadas.
Estimando o modelo VAR
Abaixo, são produzidos 3 modelos, cada um com determinado número de lags de acordo com diferentes critérios de informação (AIC, AICc e BIC).
Código
| .model | term | .response | estimate | std.error | statistic | p.value |
|---|---|---|---|---|---|---|
| var_aicc | lag(ipca,1) | ipca | 0.4022673 | 0.1082380 | 3.7165076 | 0.0003219 |
| var_aicc | lag(eipca_diff,1) | ipca | 0.4877298 | 0.2086646 | 2.3373860 | 0.0212623 |
| var_aicc | lag(selic_diff,1) | ipca | -0.0122650 | 0.1677115 | -0.0731315 | 0.9418368 |
| var_aicc | lag(ic_br_diff,1) | ipca | 0.0071756 | 0.0036690 | 1.9557476 | 0.0530779 |
| var_aicc | lag(ibc_br_sa_diff,1) | ipca | 0.0185280 | 0.0160211 | 1.1564761 | 0.2500382 |
| var_aicc | lag(ipca,2) | ipca | 0.2386245 | 0.1347311 | 1.7711171 | 0.0793622 |
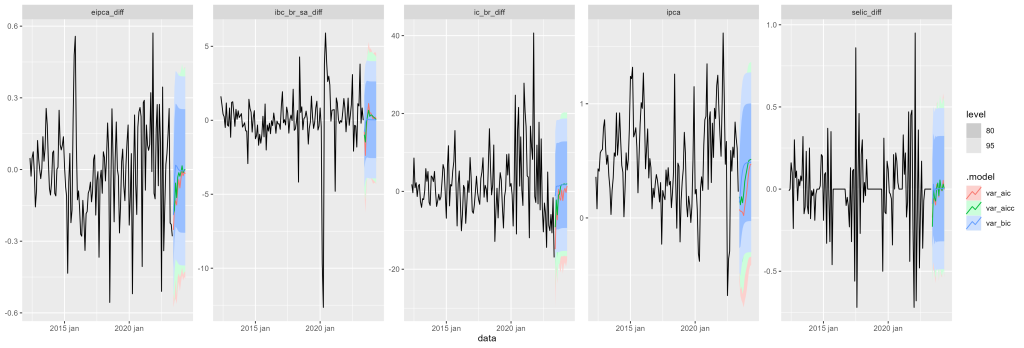
E geramos a previsão das variáveis conforme os gráficos abaixo:
___________________________________
Quer aprender mais?
Seja um aluno da nossa trilha de Macroeconomia Aplicada e aprenda a criar projetos voltados para a Macroeconomia.
Referências
Hyndman, R. J., e G. Athanasopoulos. 2013. Forecasting: Principles and Practice. OTexts.

![Rendered by QuickLaTeX.com \[z_{t} = \phi_{0} + \sum_{i=1}^{p} \phi_{i} z_{t-i} + \alpha_{t}\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-d8bf85a158f05646ab8f74d6036a13b5_l3.png)