A Lei de Okun é uma relação empírica que busca quantificar a relação entre a taxa de desemprego e a taxa de crescimento econômico. Ela foi proposta pelo economista Arthur Okun na década de 1960 e está presente em diversos livros textos de graduação. Buscamos através deste artigo investigar essa relação, descrevendo-a utilizando dados do Brasil. Usamos o Python para realizar todo o processo de análise de dados.
Para obter o código deste exercício faça parte do Clube AM e receba toda semana os códigos em R/Python, vídeos, tutoriais e suporte completo para dúvidas.
Relações empíricas relacionadas ao desemprego têm fascinado os economistas por muito tempo. Por exemplo, a curva de Phillips começou como uma simples observação de trade-off entre desemprego e inflação. No entanto, à medida que a teoria se alinhou com as evidências, a curva de Phillips emergiu como a relação mais importante na maneira como os economistas enxergam o lado da oferta da economia e está incorporada em todos os principais modelos macroeconômicos que orientam as políticas atualmente.
Outra relação de interesse para os economistas é aquela entre produção e desemprego. Em 1962, Arthur Okun observou duas relações empíricas:
- as mudanças trimestrais na taxa de desemprego estavam relacionadas ao crescimento trimestral do produto interno bruto (PIB) real
- desvios na taxa de desemprego estavam relacionados aos desvios do PIB em relação ao seu potencial (isto é, o Hiato do Produto)
Essas relações ficaram conhecidas como as versões differences e gaps da Lei de Okun, respectivamente.
A Lei de Okun é considerada uma relação estatística em vez de uma característica estrutural da economia, uma vez que tornou-se instável a sua aplicação. Isso corrobora como qualquer tipo de relação estatística, que pode estar sujeita a rupturas estruturais ou mudanças de regime. Por exemplo, mudanças estruturais no mercado de trabalho que levam a alterações na taxa de desemprego não aceleradora de inflação (NAIRU) são consideradas capazes de modificar o nível de equilíbrio do desemprego e alterar o trade-off entre inflação e produção. Embora esses choques do lado da oferta estejam cada vez mais integrados à teoria econômica, as rupturas estruturais na relação entre produção e desemprego limitaram o uso da Lei de Okun como uma regra de previsão.
Embora esses problemas tenham diminuido a confiança no uso da Lei de Okun, ainda podemos utiliza-la como uma regra de bolso simples e prática.
No presente exercício vamos empregar a Lei de Okun em sua versão output gap para dados do Brasil. O objetivo será não somente obter o coeficiente para toda a amostra, mas também criar de defasagem distribuidas e o coeficiente em janelas deslizantes.
Para dados do desemprego utilizaremos a Taxa de Desocupação medida pela PNADc ampliada e dessazonalizada, criada pelo exercício “Ampliando a série da PNADc” da Análise Macro. A importância de uma série ampliada permite que tenhamos uma amostra de tamanho suficiente, visto que utilizaremos dados trimestrais e a série da PNADc tem início em 2012.
Para dados de crescimento usamos o Hiato do Produto, capturamos os dados produzidos pelo Banco Central do Brasil, obtido através do Relatório de Inflação.
Esse artigo é uma continuação da postagem “Lei de Okun: qual a relação entre crescimento econômico e desemprego?”
Lei de Okun: output gap
Esta versão da lei relaciona as mudanças na taxa de desemprego ao hiato entre a produção real e a produção potencial ou tendencial. Portanto, se a produção cair abaixo do potencial, abrindo um hiato negativo, espera-se que o desemprego aumente. Vice-versa, quando a produção real está acima da tendência ou potencial e surge um hiato positivo, espera-se que o desemprego diminua. Semelhante à versão differences, isso enfatiza a importância do ciclo econômico na determinação das mudanças no desemprego.
Aprenda a coletar, processar, analisar e modelar dados macroeconômicos no curso de Macroeconometria usando o Python.
No entanto, não há uma definição universal do que constitui a produção ‘tendencial’ ou ‘potencial’, mas geralmente se pensa como sendo o nível de produção uma vez que medidas cíclicas e idiossincráticas foram removidas. Nesse sentido, é um nível de equilíbrio de produção no qual a economia pode crescer sem experimentar pressões inflacionárias ou deflacionárias. Outra maneira de expressar isso é definir a produção tendencial como o nível de produção consistente com o desemprego estando em sua NAIRU. Quando a produção ultrapassa a tendência, o desemprego cai abaixo de sua NAIRU e vice-versa.
Onde:
- é a taxa de desemprego no período
,
- é a taxa de desemprego no estado estacionário (ou NAIRU) no período
,
- é o PIB real no período
,
- é o PIB potencial no período
,
- é um coeficiente que representa a sensibilidade da taxa de desemprego aos desvios do PIB em relação ao seu potencial.
O problema nesta versão se concentra na impossibilidade de observar diretamente o produto potencial e a NAIRU, sendo necessário estimativas dessas medidas, o que pode tornar os valores da relação diferentes para cada diferentes método empregado para realizar a estimação.
Para o caso do Hiato, utilizaremos os dados disponibilizados pelo BCB, que estima o produto potencial através de uma função de produção. Para a NAIRU, utilizaremos o filtro hp, que permite remover oscilações, suavizando inovações de curto prazo (cíclicas e idiossincráticas).
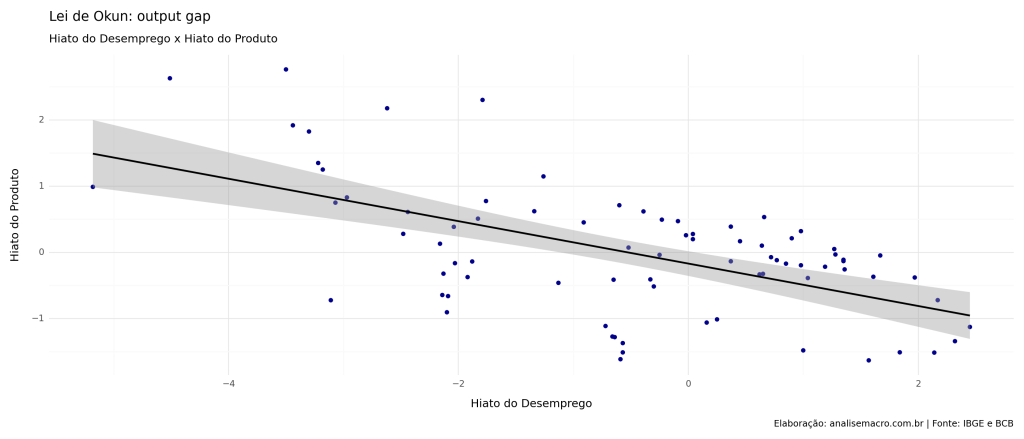
Relação output gap x hiato do desemprego
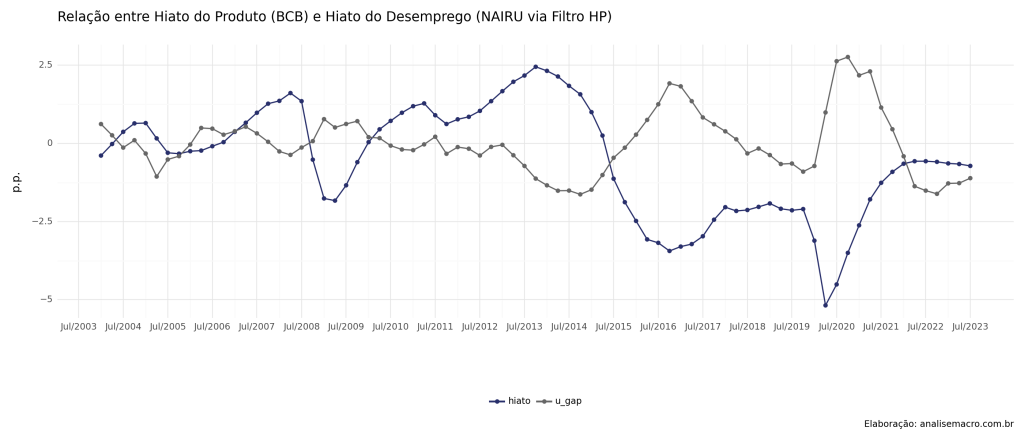
Através do gráfico de dispersão abaixo, podemos confirmar que há a relação inversa contemporânea, proposta pela Lei de Okun. Esta evidência é corroborada ao analisarmos o hiato do desemprego e do produto ao longo do tempo.
Modelo Econométrico
Modelo Estático
Código
| Dep. Variable: | u_gap | R-squared: | 0.337 |
| Model: | OLS | Adj. R-squared: | 0.328 |
| Method: | Least Squares | F-statistic: | 39.62 |
| Date: | Wed, 10 Jan 2024 | Prob (F-statistic): | 1.67e-08 |
| Time: | 20:39:02 | Log-Likelihood: | -93.763 |
| No. Observations: | 80 | AIC: | 191.5 |
| Df Residuals: | 78 | BIC: | 196.3 |
| Df Model: | 1 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
| Intercept | -0.1707 | 0.093 | -1.845 | 0.069 | -0.355 | 0.013 |
| hiato | -0.3218 | 0.051 | -6.295 | 0.000 | -0.424 | -0.220 |
| Omnibus: | 0.596 | Durbin-Watson: | 0.277 |
| Prob(Omnibus): | 0.742 | Jarque-Bera (JB): | 0.731 |
| Skew: | -0.170 | Prob(JB): | 0.694 |
| Kurtosis: | 2.678 | Cond. No. | 1.96 |
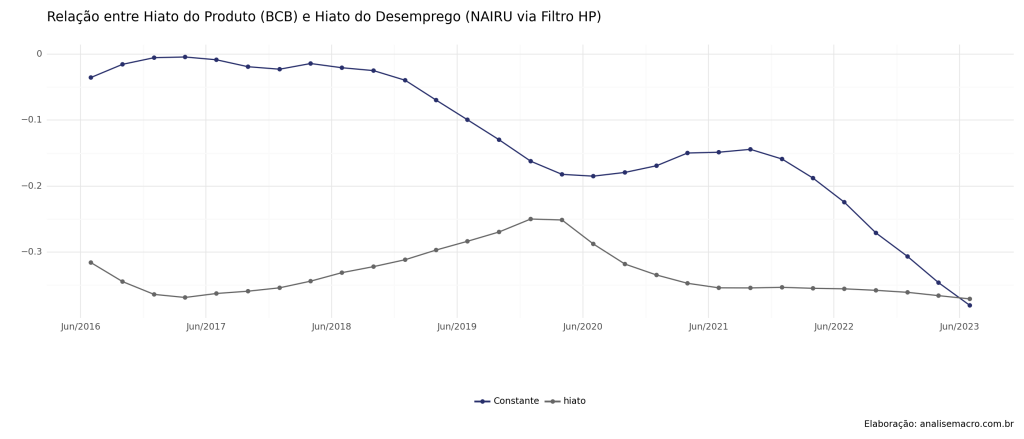
Modelo em Janelas Deslizantes
Quer aprender mais?
Clique aqui para fazer seu cadastro no Boletim AM e baixar o código que produziu este exercício, além de receber novos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas diretamente em seu e-mail.