Nós economistas, pelo menos grande parte, estamos sempre discutindo a relação entre duas ou mais variáveis e muitas vezes nos perguntamos se esta relação ainda vale ou se ela mudou ao longo do tempo. A dúvida se traduz, basicamente, em tentar descobrir se o coeficiente numa dada equação se manteve constante ao longo do tempo.
Aproveitando o post anterior (e também grande parte do script), onde assumimos o seguinte modelo para o IPCA
Podemos tentar inferir sobre a evolução do coeficiente . Obviamente existem testes formais de estabilidade de coeficientes de uma regressão (o pacote strucchange para o R, por exemplo, implementa alguns deles), porém seguindo a maneira exposta abaixo podemos ter uma intuição melhor sobre a evolução dos parâmetros (especialmente quando comparado com uma simples estatística de teste).
A idéia é então estimar o modelo proposto acima para uma dada janela, ou intervalo, de tempo, guardar os coeficientes estimados e seus respectivos desvios padrão para, em seguida, “andar” com a janela 1 mês e repetir o processo. Assim estaremos sempre utilizando o mesmo número de observações para estimar o modelo, ao mesmo tempo que fazemos uma transição lenta ao longo do tempo.
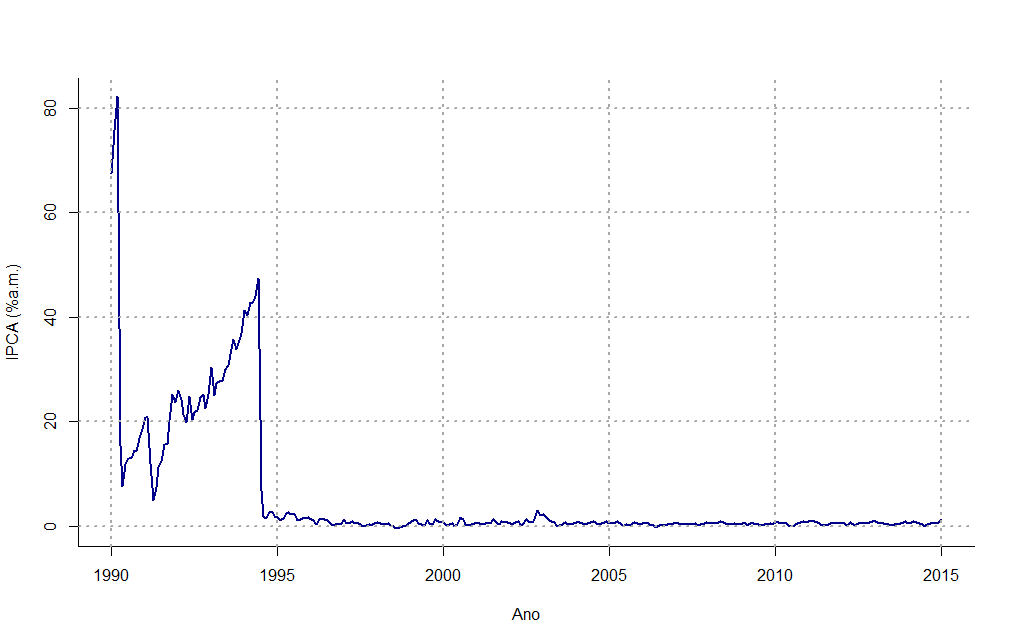
Para este exercício usarei somente o pacote lmtest (somente para simplificar a extração de informações sobre os coeficientes que eu quero) e irei ampliar a amostra do IPCA (comparado com o post anterior) para desde janeiro de 1990. Abaixo o gráfico da série utilizada e seu respectivo código de R.
plot(ipca,
ylab = 'IPCA (%a.m.)', xlab = 'Ano',
col = 'darkblue', lwd=2,
bty='l')
grid(col='darkgrey', lwd=2)
Para este exercício eu escolhi sempre utilizar uma amostra de 60 observações, isto é, 5 anos de IPCA. Em seguida eu desenvolvo um loop que faça justamente os passos expostos acima, isto é:
1. Começar com uma janela de 60 meses (em janeiro de 1990);
2. Estimar o modelo ARMA(1,1);
3. Salvar os coeficientes (e seus desvios);
4. Andar com a janela de amostra um mês para frente (isto é, começando em fevereiro de 1990);
5. Repetir os passos 1-4 até o final da amostra.
Abaixo o loop de modo a por em prática este processo.
N <- 5
inicio <- 5*freq
comp.beta <- length(ipca[inicio:length(ipca)])
k <- 3 # Numero de coeficientes
coefs <- matrix(NA, ncol=k, nrow=comp.beta)
dp <- matrix(NA, ncol=k, nrow=comp.beta)
colnames(coefs) <- c('AR','MA','Intercepto')
colnames(dp) <- c('AR','MA','Intercepto')
for (i in 1:comp.beta){
modelo <- arima(ipca[(1+i-1):(inicio+i-1)],
order = c(1,0,1))
coefs[i,] <- coef(modelo)
dp[i,] <- coeftest(modelo)[,2]
}
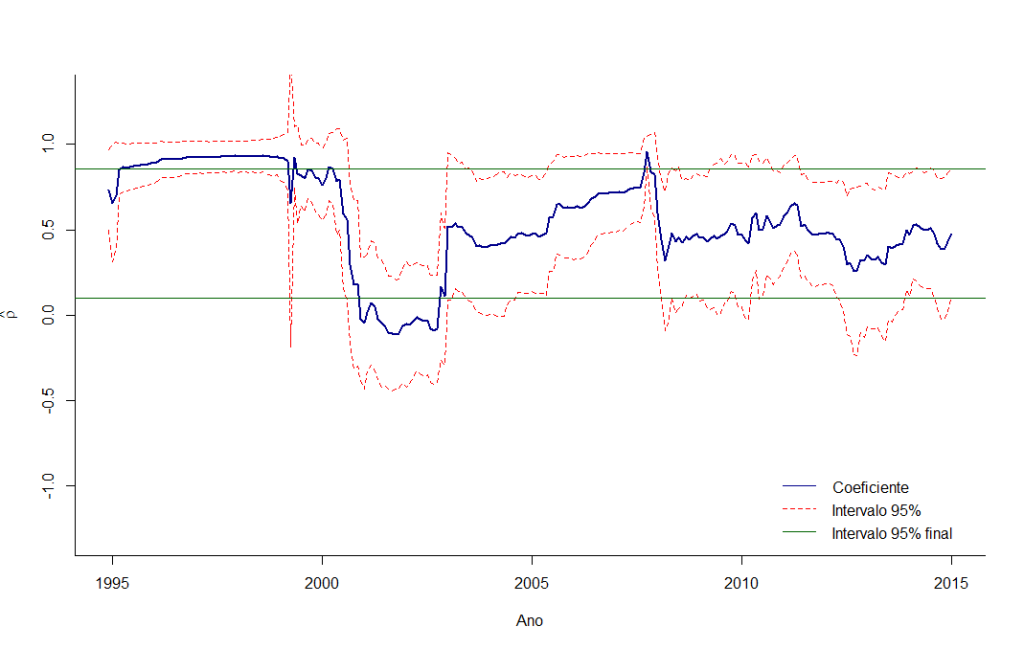
Em seguida podemos fazer um gráfico com nossas estimativas e, desta forma, ver o desenvolvimento do coeficiente de interesse (neste caso irei somente olhar para o parâmetro . Notem que no gráfico eu incluo o intervalo de confiança da última estimativa, desta forma podemos ver em quais momentos o coeficiente foi estatisticamente diferente da estimativa final, ou seja, do coeficiente hoje.
plot(coefs[,'AR'],
ylab = expression(hat(rho)), xlab = 'Ano',
col = 'darkblue', lwd=2,
ylim=c(-1.3,1.3),
bty='l')
lines(coefs[,'AR']+1.96*dp[,'AR'],
col='red',
lty=2)
lines(coefs[,'AR']-1.96*dp[,'AR'],
col='red',
lty=2)
abline(h=coefs[nrow(coefs),'AR']+1.96*dp[nrow(coefs),'AR'],
col='darkgreen',
lty=1, lwd=1)
abline(h=coefs[nrow(coefs),'AR']-1.96*dp[nrow(coefs),'AR'],
col='darkgreen',
lty=1, lwd=1)
legend('bottomright',
c('Coeficiente','Intervalo 95%','Intervalo 95% final'),
lty=c(1,2,1),
col=c('darkblue','red','darkgreen'),
bty='n')