Vetores Autoregressivos Bayesianos

Neste artigo, mostramos como é possível utilizar o Vetores Autoregressivos por meio da Abordagem Bayesiana. Como exemplo, demonstramos a estimação e previsão de série macroeconômicas utilizando o R e o Python.

Introdução

Até o momento, vimos como podemos utilizar modelos de Vetores Autoregressivos para avaliar e prever séries temporais multivariadas. Agora, veremos a abordagem Bayesiana do VAR. Entretanto, antes de verificarmos o funcionamento desse modelo e sua aplicação, realizaremos uma breve discussão sobre as diferenças da abordagem frequentista e bayesiana.

Abordagem Frequentista

Modelos estatísticos são, em geral, criados pela abordagem frequentista, no qual é amplamente utilizada para fazer inferências e tirar conclusões a partir de dados observados. Essa abordagem se concentra na análise das frequências relativas dos eventos em amostras grandes, considerando a repetição imaginária de um experimento sob as mesmas condições.

Principais características da abordagem frequentista:

Probabilidade como Frequência Relativa: Na abordagem frequentista, a probabilidade é interpretada como uma frequência relativa de um evento ocorrer em um grande número de repetições de um experimento sob as mesmas condições. Isso significa que a probabilidade de um evento é determinada observando quantas vezes ele ocorre em relação ao total de experimentos.
Estimadores Pontuais: A abordagem frequentista busca estimativas pontuais dos parâmetros desconhecidos de um modelo. Essas estimativas são baseadas em métodos como estimadores de máxima verossimilhança, que procuram encontrar os valores dos parâmetros que tornam os dados observados mais prováveis.
Inferência Baseada em Testes de Hipóteses: Os frequentistas usam testes de hipóteses para tomar decisões estatísticas. Esses testes envolvem a formulação de hipóteses nulas e alternativas, e a avaliação da probabilidade de observar os dados observados sob a hipótese nula.
Ausência de Incorporação de Conhecimento Prévio: A abordagem frequentista geralmente não incorpora informações prévias ou conhecimento especializado sobre os parâmetros do modelo. A análise é baseada exclusivamente nos dados observados.
Foco na Repetição do Experimento: A abordagem frequentista é mais adequada para situações em que é possível repetir o experimento várias vezes sob as mesmas condições. Ela é menos apropriada para situações únicas ou quando a experimentação repetida não é viável.
Ênfase na Distribuição Amostral: Os frequentistas consideram a distribuição amostral das estatísticas de amostra, como a média e o desvio padrão, para fazer inferências sobre a população.
Intervalos de Confiança: Além dos estimadores pontuais, os frequentistas também usam intervalos de confiança para fornecer uma faixa de valores prováveis para um parâmetro desconhecido.

Embora a abordagem frequentista seja amplamente utilizada e tenha uma base sólida na teoria da probabilidade, ela também tem limitações, como:

dificuldades em lidar com incerteza, a necessidade de amostras grandes para algumas inferências
falta de maneiras diretas de incorporar informações prévias.

Por isso, a abordagem frequentista é frequentemente comparada e contrastada com a abordagem bayesiana, que trata a incerteza de maneira diferente e permite incorporar informações prévias de maneira mais natural.

Abordagem Bayesiana

A abordagem bayesiana é um paradigma estatístico que trata a incerteza como uma distribuição de probabilidade e utiliza o Teorema de Bayes para atualizar gradualmente as crenças sobre os parâmetros de um modelo à medida que novas evidências são observadas. Diferentemente da abordagem frequentista, que se concentra nas frequências relativas dos eventos em amostras grandes, a abordagem bayesiana incorpora informações prévias e atuais para obter distribuições de probabilidade sobre os parâmetros e fazer inferências.

Principais características da abordagem bayesiana:

Incorporação de Incerteza: Na abordagem bayesiana, a incerteza é modelada diretamente por meio de distribuições de probabilidade. Em vez de estimativas pontuais, os parâmetros do modelo são tratados como variáveis aleatórias que têm distribuições priori (antes de observar os dados) e posteriores (após observar os dados).
Teorema de Bayes: O Teorema de Bayes é o pilar da abordagem bayesiana. Ele relaciona a probabilidade condicional inversa (probabilidade dos parâmetros dado os dados) com a probabilidade condicional direta (probabilidade dos dados dado os parâmetros) e a distribuição priori dos parâmetros.
Atualização Contínua de Crenças: À medida que novos dados são observados, as crenças sobre os parâmetros são atualizadas por meio da combinação da distribuição priori com a verossimilhança dos dados. Isso resulta em uma nova distribuição posterior dos parâmetros, que incorpora tanto o conhecimento prévio quanto os dados observados.
Incorporação de Informações Prévias: A abordagem bayesiana permite a incorporação direta de informações prévias, conhecimento especializado ou crenças sobre os parâmetros através da especificação da distribuição priori. Isso é especialmente útil quando há poucos dados disponíveis.
Interpretação Direta da Incerteza: As distribuições posteriores dos parâmetros fornecem uma interpretação direta da incerteza associada a esses parâmetros. Intervalos de credibilidade, por exemplo, representam faixas de valores prováveis para os parâmetros.
Inferência Hierárquica: A abordagem bayesiana pode ser usada para modelar hierarquias complexas, incorporando incerteza em múltiplos níveis de um modelo.
Processamento Computacional Intensivo: A inferência bayesiana muitas vezes envolve técnicas computacionais, como Cadeias de Markov Monte Carlo (MCMC), para amostragem de distribuições posteriores.

Teorema de Bayes

O Teorema de Bayes é um princípio fundamental na teoria das probabilidades e é usado para atualizar probabilidades após a observação de novas evidências. Ele estabelece a relação entre a probabilidade condicional inversa (probabilidade de uma hipótese ser verdadeira dado um conjunto de dados) e a probabilidade condicional direta (probabilidade dos dados dado uma hipótese). O teorema é nomeado em homenagem ao matemático e estatístico britânico Thomas Bayes, que desenvolveu o conceito.

A forma geral do Teorema de Bayes é a seguinte:

$P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)}$

Onde:
- $P(A|B)$ é a probabilidade de um evento $A$ ocorrer dado que o evento $B$ ocorreu (probabilidade posterior).
- $P(B|A)$ é a probabilidade de um evento $B$ ocorrer dado que o evento $A$ ocorreu (probabilidade de verossimilhança).
- $P(A)$ é a probabilidade a priori do evento $A$ ocorrer (probabilidade a priori).
- $P(B)$ é a probabilidade marginal do evento $B$ ocorrer.

Em termos mais simples, o Teorema de Bayes nos diz como atualizar nossas crenças sobre um evento à medida que novas evidências são apresentadas. Começamos com uma crença inicial (probabilidade a priori) e, à medida que observamos mais informações (probabilidade de verossimilhança), ajustamos nossa crença inicial para chegar a uma nova crença atualizada (probabilidade posterior).

VAR Bayesianos

Os Vetores Autoregressivos Bayesianos (VAR Bayesianos) são modelos estatísticos utilizados para analisar e prever séries temporais multivariadas, onde múltiplas séries temporais são modeladas simultaneamente com base em suas relações passadas e informações prévias. No caso, o VAR pode ser modelagem através da abordagem Bayesiana.

Considere $p$ séries temporais $y_t = (y_{1,t}, y_{2,t}, \ldots, y_{p,t})^T$ observadas em $t = 1, 2, \ldots, T$ , onde $p$ é o número de séries temporais e $T$ é o número de observações.

Um VAR Bayesiano de ordem $q$ é especificado da seguinte forma:

$y_t = c + A_1 y_{t-1} + A_2 y_{t-2} + \dots + A_q y_{t-q} + \varepsilon_t$

Onde:

- $y_t$ é um vetor $p \times 1$ contendo as observações das $p$ séries temporais no tempo $t$ .
- $c$ é um vetor $p \times 1$ de termos constantes.
- $A_1, A_2, \ldots, A_q$ são matrizes $p \times p$ de coeficientes associados aos termos defasados das séries temporais.
- $\varepsilon_t$ é um vetor $p \times 1$ de resíduos aleatórios, assumindo-se tipicamente que os resíduos seguem uma distribuição multivariada normal.

Na abordagem bayesiana, os coeficientes $A_i$ e o vetor de constantes $c$ são tratados como variáveis aleatórias e são modelados usando distribuições priori. A partir dos dados observados e das distribuições priori, a distribuição posterior dos parâmetros é obtida usando o Teorema de Bayes. Amostras desses parâmetros são então geradas usando técnicas de amostragem, como Cadeias de Markov Monte Carlo (MCMC).

Essa estrutura permite que os VAR Bayesianos capturem as relações dinâmicas e interações entre as séries temporais, enquanto incorporam incerteza através das distribuições priori e posteriores.

Para obter todo o código em R e Python para os exemplos abaixo, faça parte do Clube AM, o repositório de códigos da Análise Macro, contendo exercícios semanais.

BVAR com o R

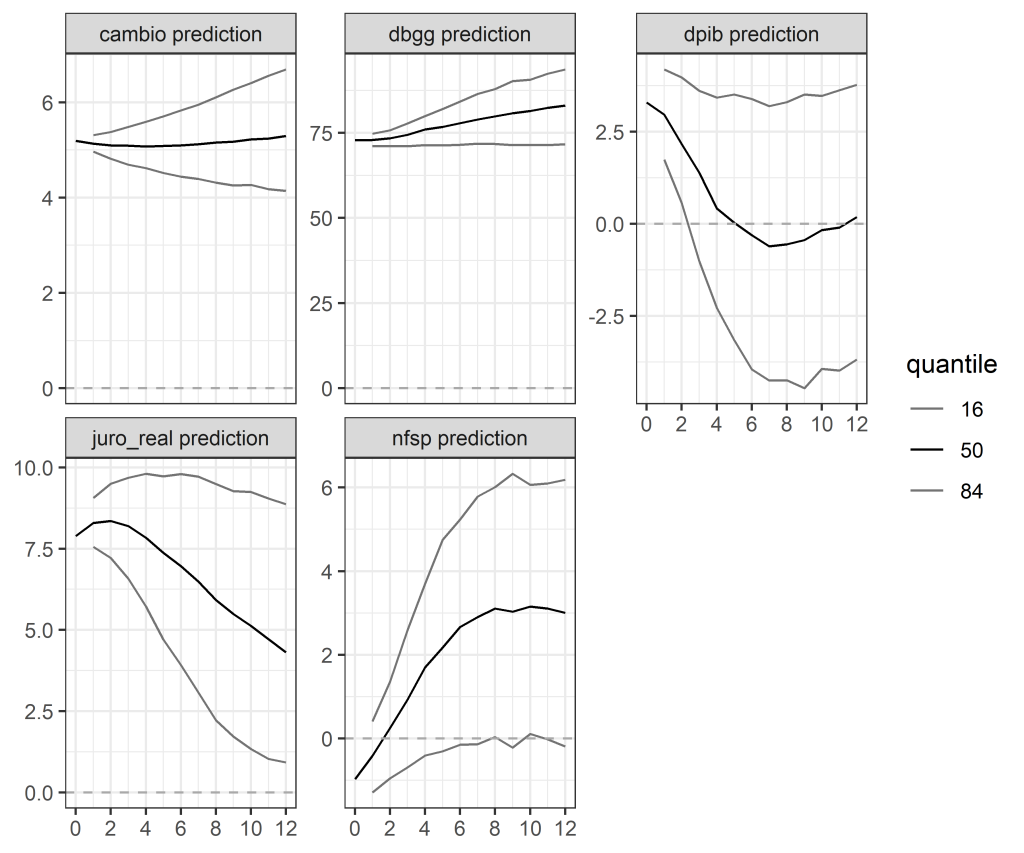
Podemos aplicar um exemplo de construção do BVAR usando o R como ferramenta através dos pacotes {BVAR} e {BVARverse}. Como exemplo, usamos a variáveis câmbio, DBGG, PIB, Juro Real ex-post e NFSP. Abaixo, um gráfico da previsão de cada variável.

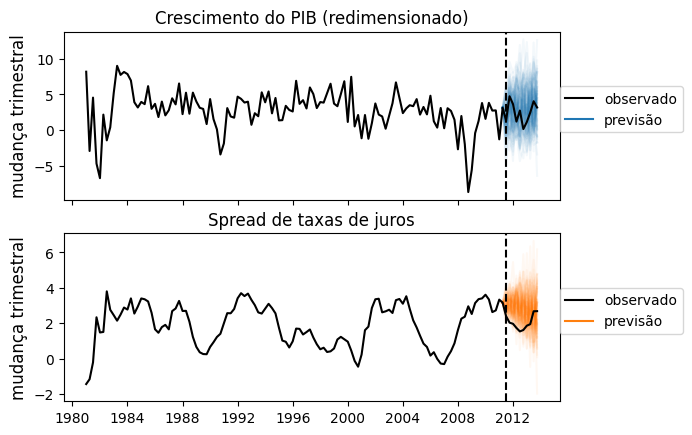
BVAR com o Python

Com o Python, realizamos o uso da biblioteca pymc3, que permite criar equações de modelos bayesianos. Como exemplo, usamos dados do Spread de taxa de juros e Crescimento do PIB dos EUA.

___________________________________
Quer aprender mais?

Seja um aluno da nossa trilha de Macroeconomia Aplicada e aprenda a criar projetos voltados para a Macroeconomia.

Referências

Ricardo Vieira. Bayesian Vector Autoregression in PyMC. PyMc Labs. 24/06/2022. Disponível em https://www.pymc-labs.io/blog-posts/bayesian-vector-autoregression/. Acesso em 14/08/2023.

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais
e conteúdos exclusivos sobre Análise de Dados!

Assinar

Encontre o seu conteúdo

Categorias

Artigos mais acessados

A Abordagem do Estudo de Eventos usando Python

Análise regional da atividade econômica com dados do BCB usando Python

Como coletar dados do Eurostat usando a API com o Python?

Estimando a volatilidade da taxa de câmbio

Como analisar o Núcleo de Inflação no Brasil usando Python?

Propensity Score com Múltiplas Variáveis no R

Outros artigos relacionados

A Abordagem do Estudo de Eventos usando Python

A maioria das pesquisas em finanças está dedicada a investigar o efeito de um anúncio da companhia ou de um evento, sistêmico ou não, sobre o preço de uma ação. Esses estudos são conhecidos como “estudos de eventos”. Neste contexto, apresentaremos uma breve introdução à metodologia e demonstraremos como aplicá-la por meio de exemplos reais utilizando a linguagem de programação Python.

Análise regional da atividade econômica com dados do BCB usando Python

O Banco Central disponibiliza indicadores regionais sobre a atividade econômica, possibilitando análises a nível de regiões e estados brasileiros. Neste artigo mostramos como acessar, processar e analisar estes dados utilizando o Python.

Como coletar dados do Eurostat usando a API com o Python?

Neste artigo mostramos como pesquisar e como coletar os dados do portal Eurostat através do sistema de API usando a linguagem Python. Este processo permite automatizar rotinas de extração de dados, eliminando trabalho manual e repetitivo de atualização de bases de dados econômicos.

Vetores Autoregressivos Bayesianos

Introdução

Abordagem Frequentista

Abordagem Bayesiana

Teorema de Bayes

VAR Bayesianos

BVAR com o R

BVAR com o Python

___________________________________ Quer aprender mais?

Referências

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Outros artigos relacionados

___________________________________
Quer aprender mais?