Uma das perguntas que mais tem sido feita aos economistas ultimamente é quando o desemprego vai começar a subir. Não é desejo das pessoas que perguntam, mas apenas constatação acaciana: afinal, economia que não cresce não gera emprego. E a resposta tem sido "depende". Depende de como a procura por trabalho vai se comportar daqui para frente. Isto porque, o desemprego é função de dois componentes principais: da oferta e demanda por mão de obra. Se a demanda cai por conta do baixo crescimento e a oferta se mantém, o desemprego sobe. Entretanto, se ambas caem, o desemprego pode até cair, se a oferta cair mais do que a demanda. Logo, a taxa de desemprego pode não estar sinalizando corretamente o que está acontecendo no mercado de trabalho, ainda que os salários continuem crescendo.
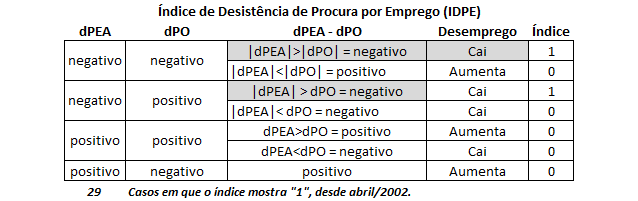
Pois é. No ano passado eu toquei várias vezes no assunto nesse espaço. Cheguei, inclusive, a criar um índice que busca identificar quando o desemprego está caindo mais por influência da queda na procura por emprego do que por influência da demanda por mão de obra. Em 2014, isso aconteceu 4 vezes: Na série da PME, desde abril de 2002 (153 observações), esse "fênomeno" aconteceu 29 vezes (18%).
E em 2015, como será? Bom, para tentar responder essa pergunta difícil nada melhor do que usar um pouco de econometria, não é mesmo? Para tal, vamos usar três séries extraídas da PME (Pesquisa Mensal de Emprego) do IBGE, disponível no amigável SIDRA: a taxa de desemprego, a variação interanual da população ocupada e da população economicamente ativa. Estas duas últimas são calculadas, logicamente, a partir dos dados de PO e PEA. Vamos construir um modelo ARIMA utilizando o R.
Antes de mais nada, vamos ver as séries. Os códigos e gráficos são colocados abaixo.
### Gráfico da Taxa de Desemprego
plot(desemprego[,'desemprego'], col='red', xlab='', ylab='%',
xlim=c(2003,2015), bty='l', lwd=3, lty=1)
grid(lty=2, lwd=1, col='darkgrey')
mtext('Desemprego no Brasil pela PME-IBGE',side=3,line=1, col='black',
font=2)
mtext('Fonte: [analisemacro.com.br], com dados do IBGE.',
side=1,line=3)
### Gráfico das variáveis exógenas
par(mar=c(5,4,4,5)+.1)
plot(desemprego[,'pea'],type='l',col='red', lty=2, lwd=2,
xlab='', ylab='PEA', ylim=c(-1,7), main='')
par(new=T)
plot(desemprego[,'po'], type='l', col='black',
xaxt='n',yaxt='n', lty=1, lwd=2,
xlab='', ylab='', ylim=c(-1,6))
axis(4)
mtext('PO',side=4,line=3)
legend('topright', col=c('red','black'), lty=c(2,1),
lwd=c(2,2), legend=c('PEA', 'PO'))
mtext('PEA vs. PO',side=3,line=2, col='black',
font=2)
mtext('(variaçao interanual)',side=3,line=1, col='black',
font=1)
mtext('Fonte: [analisemacro.com.br], com dados do IBGE.',
side=1,line=3)
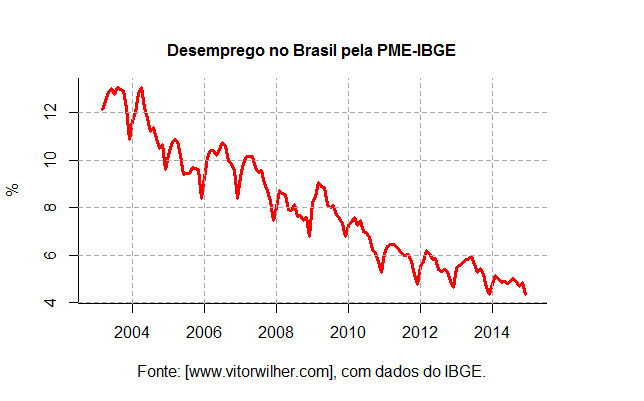
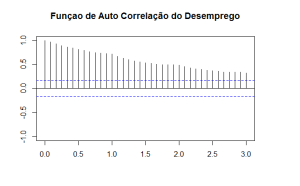
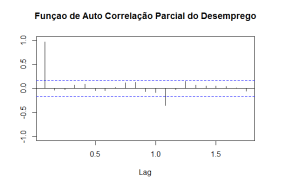
Bom, ao visualizar o gráfico do desemprego é nítido que ele apresenta um comportamento sazonal ao longo do ano. Ele aumenta nos primeiros meses e cai nos últimos, refletindo o comportamento cíclico da economia. Esse é um aspecto importante na hora de constuir o ARIMA. Para uma ideia sobre qual modelo escolher, vamos dar uma olhada nos correlogramas da taxa de desemprego com as funções acf e pacf.
Ao olhar os correlogramas, fica nítido que a taxa de desemprego apresenta uma "inércia", com o coeficiente da primeira defasagem próximo a 1. Além disso, observa-se que, de fato, a sazonalidade que vimos no gráfico é mesmo significativa. Para completar as informações que dispomos até aqui, falta verificar a ordem de integração da taxa de desemprego. Para isso, é necessário rodar alguns testes de raiz unitária para verificar se a série em questão é ou não estacionária (possui média e variância constantes). No caso do desemprego, ao olhar o gráfico, é bastante nítido que a mesma possui uma tendência decrescente ao longo da amostra considerada. Isso é um indício de que a mesma não é estacionária ou é estacionária ao redor de uma tendência.
Um teste mais elaborado de raiz unitária pode ser feito adotando algum protocolo ou aplicando testes tradicionais, como "adf", "kpss" e "pp", de forma a tentar inferir qual a ordem de integração da série. Para isso, é preciso verificar a ordem de defasagem da equação de teste, de forma a controlar a autocorrelação dos resíduos, o poder do teste com a inclusão de variáveis determinísticas, o tamanho da amostra para testes como o "df-gls" e "ng-perron" e por aí vai. Como o post não é sobre raiz unitária, vamos simplesmente considerar que a série é integrada de ordem 1, isto é, possui uma raiz unitária. Isso, o leitor pode tratar com maiores pormenores alterando o script ao final do texto.
Dito isto, vamos comparar dois modelos. O primeiro será extraído da função auto.arima do pacote forecast, enquanto o segundo será um SARIMA (1,1,1)(1,1,1). Além disso, vamos considerar nos dois modelos como variáveis exógenas a variação interanual da população ocupada e da população economicamente ativa. Para isso, vamos rodar o seguinte código.
### Construção dos modelos ARIMA ### xreg <- window(cbind(desemprego[,'po'],desemprego[,'pea']), end=prev.start-c(0,1)) newxreg <- window(cbind(desemprego[,'po'],desemprego[,'pea']), start=prev.start) modelo01 <-auto.arima(window(desemprego[,"desemprego"], end=prev.start-c(0,1)), xreg=xreg, max.p=5, max.q=5, max.P=2, max.Q=2, trace=F) modelo02<-arima(window(desemprego[,"desemprego"], end=prev.start-c(0,1)), order=c(1,1,1), seasonal=list(order=c(1,1,1),period=12), xreg=xreg)
Feito isto, podemos dar uma olhada nos modelos com o comando summary().
> summary(modelo01) Series: window(desemprego[, "desemprego"], end = prev.start - c(0, 1)) ARIMA(3,1,0)(2,0,0)[12] Coefficients: ar1 ar2 ar3 sar1 sar2 desemprego[, "po"] -0.1369 0.0811 -0.0005 0.8087 0.0437 -0.4319 s.e. 0.0814 0.0789 0.0776 0.0758 0.0738 0.0241 desemprego[, "pea"] 0.4465 s.e. 0.0230 sigma^2 estimated as 0.02541: log likelihood=58.44 AIC=-101.96 AICc=-100.86 BIC=-78.37 > summary(modelo02) Series: window(desemprego[, "desemprego"], end = prev.start - c(0, 1)) ARIMA(1,1,1)(1,1,1)[12] Coefficients: ar1 ma1 sar1 sma1 desemprego[, "po"] desemprego[, "pea"] 0.5827 -0.5918 0.6367 -0.9996 -0.4235 0.4284 s.e. NaN NaN 0.0942 0.4028 0.0272 0.0260 sigma^2 estimated as 0.03201: log likelihood=34.64 AIC=-55.28 AICc=-54.35 BIC=-35.26
Feito isto, é importante dar uma olhada nos resíduos dos modelos para ver se estão "bem comportados". Pode-se ver a normalidade dos resíduos com o comando jarque.bera.test e a autocorrelação com o Box.test. Neste último, entretanto, é preciso corrigir os graus de liberdade, dado que o mesmo não foi feito para verificar os resíduos de uma regressão. Maiores detalhes, no script ao final do post. Para o caso aqui sublinhado, os resíduos estão ok. Logo, é hora de fazer a previsão propriamente dita com o comando forecast do pacote de mesmo nome. Um detalhe importante é que estou assumindo que entre janeiro e dezembro de 2015, a população ocupada e população economicamente ativa irão crescer conforme uma média dos últimos anos. De forma alternativa, você pode gerar uma previsão para essas variáveis, antes de prever a taxa de desemprego propriamente dita.
### Previsão ### prev1 <- forecast(modelo01, 12, level=40, xreg=newxreg) prev2 <- forecast(modelo02, 12,level=40, xreg=newxreg)
Após tudo isso, abaixo construímos uma tabela com os resultados dos dois modelos.
### Construindo matriz com resultados das previsões ### prevmean<-cbind(prev1$mean[1:12],prev2$mean[1:12]) prevlower<-cbind(prev1$lower[1:12],prev2$lower[1:12]) prevupper<-cbind(prev1$upper[1:12],prev2$upper[1:12]) prevtot<-cbind(prevlower,prevmean,prevupper) write.csv2(cbind(prevlower,prevmean,prevupper), file="prevdesemprego.csv")
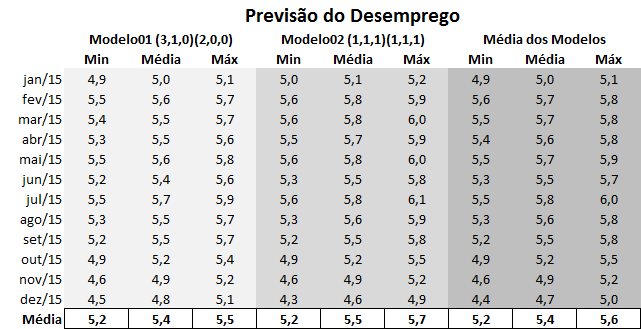
E abaixo organizada a tabelinha com os resultados para os próximos 12 meses.
Pois é, a média dos modelos indica que o desemprego deve ficar em 5,4% em 2015, o que seria 0,6 pontos percentuais acima do registrado em 2014. A tendência de aumento, ao menos, parece ser capturada por ambos os modelos. O leitor pode tentar outras coisas, como por exemplo, tentar inferir o comportamento da população ocupada e da população economicamente ativa. Ou, claro, utilizar outras variáveis exógenas, considerar a taxa de desemprego trend stationary, etc. Para além disso, o exercício tem objetivo meramente didático, logo deve ser visto com cautela. Para projeções mais apuradas, que levem em consideração outras questões que afetam o mercado de trabalho, basta entrar em contato... 🙂
O script do exercício aqui.