[et_pb_section admin_label="section"][et_pb_row admin_label="row"][et_pb_column type="1_2"][et_pb_text admin_label="Texto" background_layout="light" text_orientation="justified" use_border_color="off" border_color="#ffffff" border_style="solid" text_font="Verdana||||" text_font_size="18"]
No post anterior, fizemos um apanhado sobre como coletar e tratar dados agregados do INSS com uso do R. Nesse, vamos discutir uma característica que salta aos olhos em relação à série de gasto previdenciário: o fato da mesma não ser estacionário. É, por suposto, o tipo de discussão inicial que fazemos em nosso curso de Séries Temporais usando o R. Para começar, coloco abaixo o gráfico com o gasto mensal com INSS, em valores correntes.
[/et_pb_text][/et_pb_column][et_pb_column type="1_2"][et_pb_image admin_label="Imagem" src="https://analisemacro.com.br/wp-content/uploads/2019/02/loteextra2.png" show_in_lightbox="off" url="https://analisemacro.com.br/cursos-de-r" url_new_window="off" use_overlay="off" animation="left" sticky="off" align="left" force_fullwidth="off" always_center_on_mobile="on" use_border_color="off" border_color="#ffffff" border_style="solid"]
[/et_pb_image][/et_pb_column][/et_pb_row][et_pb_row admin_label="row"][et_pb_column type="4_4"][et_pb_text admin_label="Texto" background_layout="light" text_orientation="justified" use_border_color="off" border_color="#ffffff" border_style="solid" text_font="Verdana||||" text_font_size="18"]
Ao olhar a série acima, chama atenção a tendência da mesma. Significa dizer que se estivéssemos interessados em modelar a série, teríamos de levar essa tendência crescente em consideração. Isso é, de fato, um problema. Para entendermos melhor essa questão, vamos definir o que seja uma série estacionária.
Com base em Enders (2009), podemos assumir que um processo estocástico, tendo uma média e variância finitas, será covariância-estacionário se para todos 
e 
,
(1) ![\begin{eqnarray*} E(y_{t}) = E(t-k) = \mu \\ E\left [(y_{t} - \mu)^2 \right ] = E\left [(y_{t-k} - \mu)^2 \right ] = \sigma_{y}^2 \\ E\left [(y_{t} - \mu)(y_{t-k} - \mu) \right ] = E\left [(y_{t-j} - \mu)(y_{t-j-k} - \mu) \right ] = \gamma_{k} \end{eqnarray*}](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-a350d0e5c212cacde204471e6fa6c497_l3.png "Rendered by QuickLaTeX.com")
onde 
, 
e 
são todas constantes. Em termos simples, desse modo, uma série temporal é covariância-estacionária se sua média e todas as auto-covariâncias não são afetadas por mudanças na origem do tempo.
Em outras palavras, como explica Wooldridge (2013), a estacionariedade da covariância enfatiza somente os primeiros dois momentos de um processo estocástico: a média e a variância do processo são constantes no decorrer do tempo e a covariância entre 
e 
depende somente da distância entre os dois termos, h, e não da localização do período de tempo inicial.
Com base nessa definição e olhando para a nossa série de gasto previdenciário, não parece em nada com um processo estacionário, não é mesmo? Pois é, para tirar a prova dos nove, aplicamos o teste ADF Sequencial, proposto, por exemplo, por Pfaff (2008). Uma vez feito isso, descobre-se que se trata de um processo tendência-estacionário. Para ilustrar melhor o argumento, podemos, por suposto, caracterizar uma série tendência-estacionária como segue:
(2) 
Onde 
forma uma tendência determinística e 
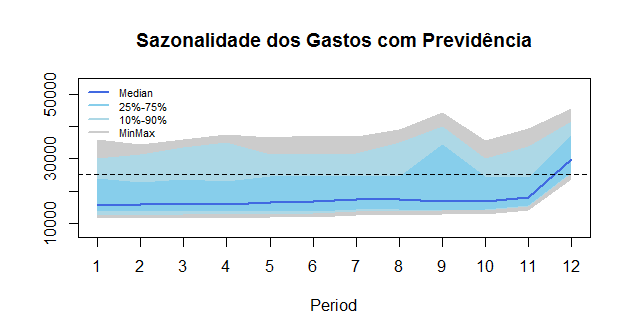
representa um componente estocástico. Isso significa que para tornarmos estacionária, precisamos retirar o componente determnístico, deixando apenas . Ademais, observamos que a série apresenta sazonalidade, como pode ser visto melhor no gráfico abaixo.
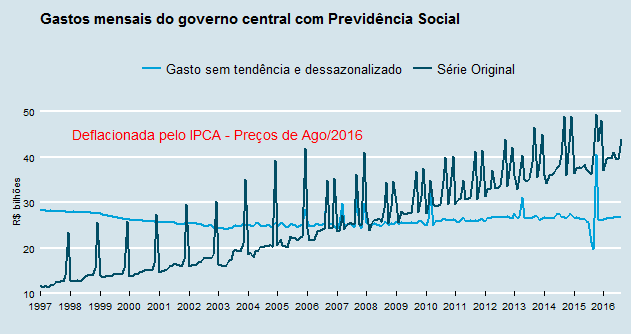
A sazonalidade vem, basicamente, do décimo-terceiro salário. Uma vez compreendido que se trata de uma série tendência-estacionária e que contém sazonalidade, nós tratamos os dois problemas e apresentamos abaixo a série original comparada à série sem tendência e dessazonalizada.
Bem diferente, não é mesmo? A tendência positiva contida no gasto com previdência nos indica, portanto, que o mesmo é uma série não estacionária, que irá crescer de forma indefinida, se nada não for feito. Por isso, é tão importante realizar uma reforma no sistema.
Para saber mais sobre o tipo de análise que fizemos nesse post, confira nosso curso de Séries Temporais usando o R!
[/et_pb_text][/et_pb_column][/et_pb_row][/et_pb_section]
