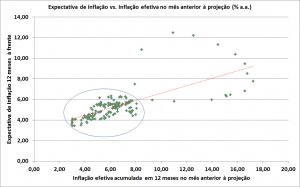
Ontem, o Comitê de Política Monetária decidiu, por unanimidade, elevar a taxa básica de juros, a Selic, em 50 pontos-base, de 10% para 10,5%. Na minha leitura pesou na decisão dos membros do comitê o IPCA divulgado na última semana, mostrando uma inflação bastante disseminada pelos 365 bens e serviços que compõem o índice, com a difusão beirando os 70%. A despeito dos problemas de comunicação da autoridade monetária, notadamente ao explicitar as defasagens envolvidas no processo e a indecisão sobre o cenário fiscal, observo que a Selic deve ir mesmo a 11% na próxima reunião, como havia projetado na Carta de Dezembro e no cenário normativo da Carta de Janeiro. O Banco Central, com essa decisão, mostrou que não abandonou, ainda, a ancoragem das expectativas - que só cederão quando a inflação efetiva mostrar algum alívio, como pode ser visto no gráfico ao lado. As pressões remanescentes sobre o índice, como a desvalorização do câmbio e o contínuo crescimento da massa salarial, são desafios para o movimento contracionista. A minha leitura, nesse ponto, é que o Banco faça mais um ajuste de 50 pontos-base em fevereiro e suste o processo, verificando a transmissão sobre os principais canais (expectativas, notadamente). A aguardar a ata na próxima semana para confirmar essa leitura. O bom-senso, leitor, venceu: ao menos, por enquanto.
