A análise de correlação desempenha um papel importante na análise de séries temporais, dado que pode ser útil como indicativo de relação entre os valores passados de uma variável.
Neste artigo, vamos apresentar o conceito de autocorrelação na estatística, avaliar sua aplicabilidade no mundo real, verificar como estimar e interpretar e, por fim, vamos ver como aplicar a análise de autocorrelação com dados macro-financeiros do Brasil, usando as linguagens de programação R e Python.
O que é autocorrelação?
Na análise de séries temporais, a autocorrelação é qualquer relação estatística, causal ou não, entre os valores passados com os valores presentes de uma variável aleatória.
Mas o que isso significa? Em termos técnicos, a autocorrelação mede a correlação entre os valores de uma série de dados com seus próprios valores defasados no tempo (valor da observação no índice contra o índice
,
,
). Em outras palavras, a autocorrelação avalia a relação entre observações consecutivas em uma série temporal.
Usualmente, utiliza-se de duas medidas para o cálculo da autocorrelação, a Função de Autocorrelação (FAC/ACF) e a Função de Autocorrelação Parcial (FACP/PACF), que exploraremos melhor adiante.
Também é importante notar que a autocorrelação aqui só mede a relação linear entre duas variáveis. Variáveis que se relacionam de forma não linear não podem ser captadas corretamente, sendo necessário utilizar medidas apropriadas para analisar essas relações.
Quando usar usar a autocorrelação?
A autocorrelação possui uma especificidade maior que a correlação, visto que pretende-se analisar a relação de uma série temporal com ela mesma. Entretanto, apesar de estar em um nicho mais estreito, o seu uso é de extrema importância, pois pode auxiliar a encontrar padrões importantes e auxiliar na montagem de modelos estatísticos. Alguns exemplos:
- Finanças: A autocorrelação é frequentemente usada para analisar séries temporais financeiras. Ela ajuda a identificar padrões e tendências nos retornos dos ativos financeiros, permitindo a construção de modelos de previsão e Volatilidade.
- Economia: Permite avaliar se existe alguma inércia em determinada variável, como por exemplo, na identificação da inércia inflacionária. Além disso, auxilia a analisar modelos econométricos, permitindo encontrar tendências e sazonalidade em séries temporais.
- Meteorologia e Ciências Ambientais: Auxilia analisar dados climáticos e ambientais, como temperaturas, precipitação e níveis de poluentes ao longo do tempo. Isso ajuda a identificar padrões sazonais, tendências de longo prazo e fenômenos climáticos recorrentes, como El Niño e La Niña.
- Processamento de Sinais: A autocorrelação é amplamente utilizada no processamento de sinais para análise e detecção de padrões. Por exemplo, na área de telecomunicações, a autocorrelação é usada para estimar atrasos de propagação de sinais em um canal de comunicação e para a detecção de sinais periódicos.
Como calcular a correlação entre duas variáveis?
Existe mais dois métodos diferentes de medir a autocorrelação, temos o ACF e o PACF. Vamos verificar o primeiro caso.
O **FAC** mede a relação linear e é comumente denotado com os símbolos (rho) ou
para medir o grau de correlação de uma observação passada com o valor presente, em que o índice
representa o número da defasagem.
O FAC pode ser calculado pela divisão da covariância dos valores presentes e dos valores da defasagem pelo desvio padrão.
A fórmula matemática para calcular o ACF () é:
onde:
representa o índice no tempo da observação da variável.
é o tamanho da série temporal;
são os valores individuais das observações em cada ponto do tempo
da variável em questão.
é a média amostral de
.
No caso, teremos diversos coeficientes de autocorrelação de tamanho . Por exemplo,
mede a relação entre
e
,
mede a relação entre
e
e assim em diante.
As imagens abaixo ilustram bem o caso.
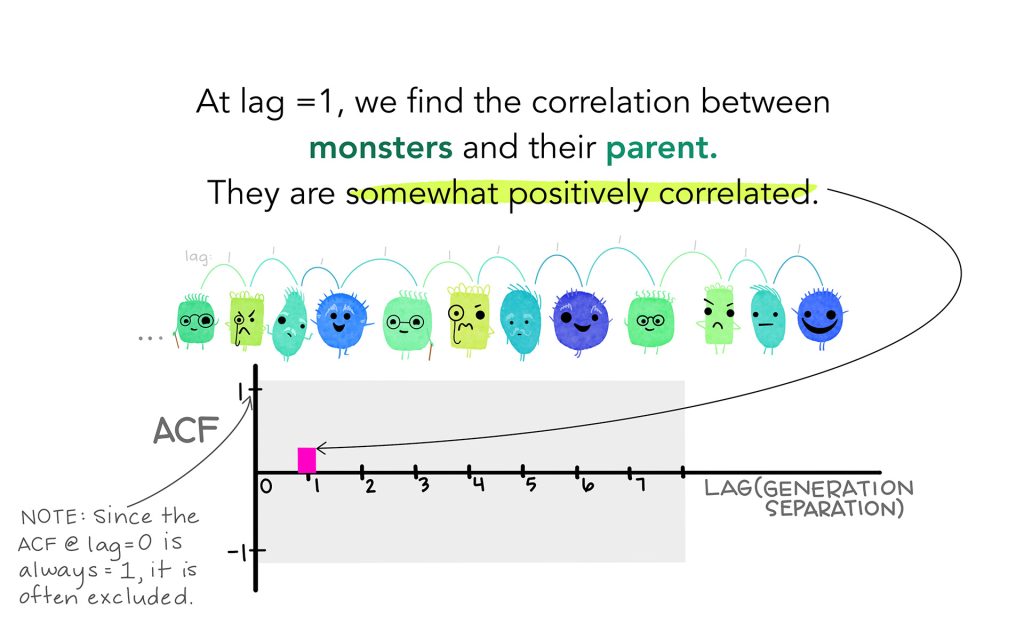

Como interpretar o valor da autocorrelação?
O coeficiente de autocorrelação pode assumir valores na mesma medida que o coeficiente de correlação de Pearson. Portanto, implica que a correlação entre dos valores passados pode ser negativa, positiva ou nula, além de indicar, informalmente, a força da relação linear.
Podemos indicar o guia de mensuração do grau de autocorrelação:
- ±0.9 a ±1 indica correlação muito forte
- ±0.7 a ±0.9 indica correlação forte
- ±0.5 a ±0.7 indica correlação moderada
- ±0.5 a ±0.3 indica correlação fraca
- ±0.3 a 0 indica correlação desprezível ou nula
Exemplo prático: correlação entre variáveis macro-financeiras
Para fixar o conhecimento de forma aplicada usando ferramentas práticas de linguagem de programação, abaixo calculamos o coeficiente de autocorrelação das variáveis “taxa de juros Selic” e “taxa de inflação IPCA”, período 2005 a 2023. A fonte dos dados é o BCB e o IBGE.
Para obter todo o código em R e Python para os exemplos abaixo, faça parte do Clube AM, o repositório de códigos da Análise Macro, contendo exercícios semanais.
Para o caso do R, utilizaremos o framework do Tidyverts, uma família de pacotes que facilita a criação de análise e previsão de séries temporais.
No Python, veremos como construir através do uso de funções da biblioteca statsmodels.
R
Código
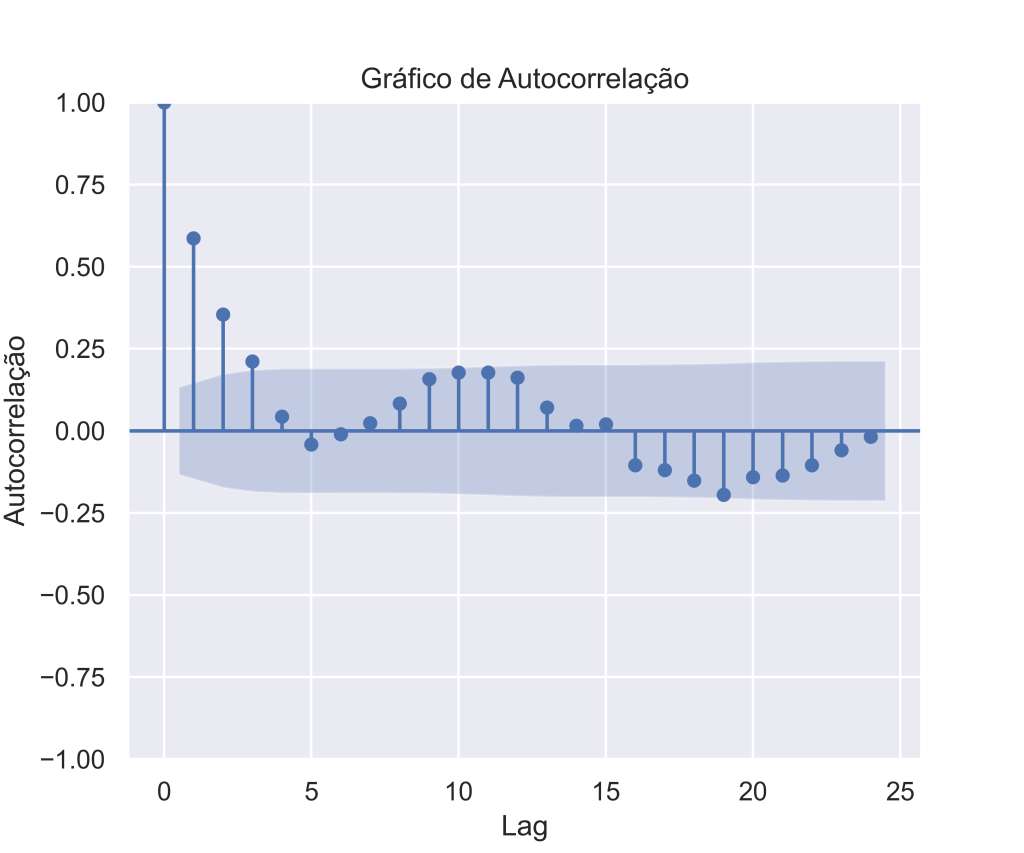
| lag | acf |
|---|---|
| 1M | 0.5860022 |
| 2M | 0.3539921 |
| 3M | 0.2112729 |
| 4M | 0.0430643 |
| 5M | -0.0412319 |
| 6M | -0.0105816 |
| 7M | 0.0237349 |
| 8M | 0.0829602 |
| 9M | 0.1576327 |
| 10M | 0.1773623 |
| 11M | 0.1771891 |
| 12M | 0.1616305 |
| 13M | 0.0708879 |
| 14M | 0.0159120 |
| 15M | 0.0197167 |
| 16M | -0.1045384 |
| 17M | -0.1196631 |
| 18M | -0.1518746 |
| 19M | -0.1948830 |
| 20M | -0.1409027 |
| 21M | -0.1362136 |
| 22M | -0.1050327 |
| 23M | -0.0590058 |
| 24M | -0.0184417 |
Código
Código
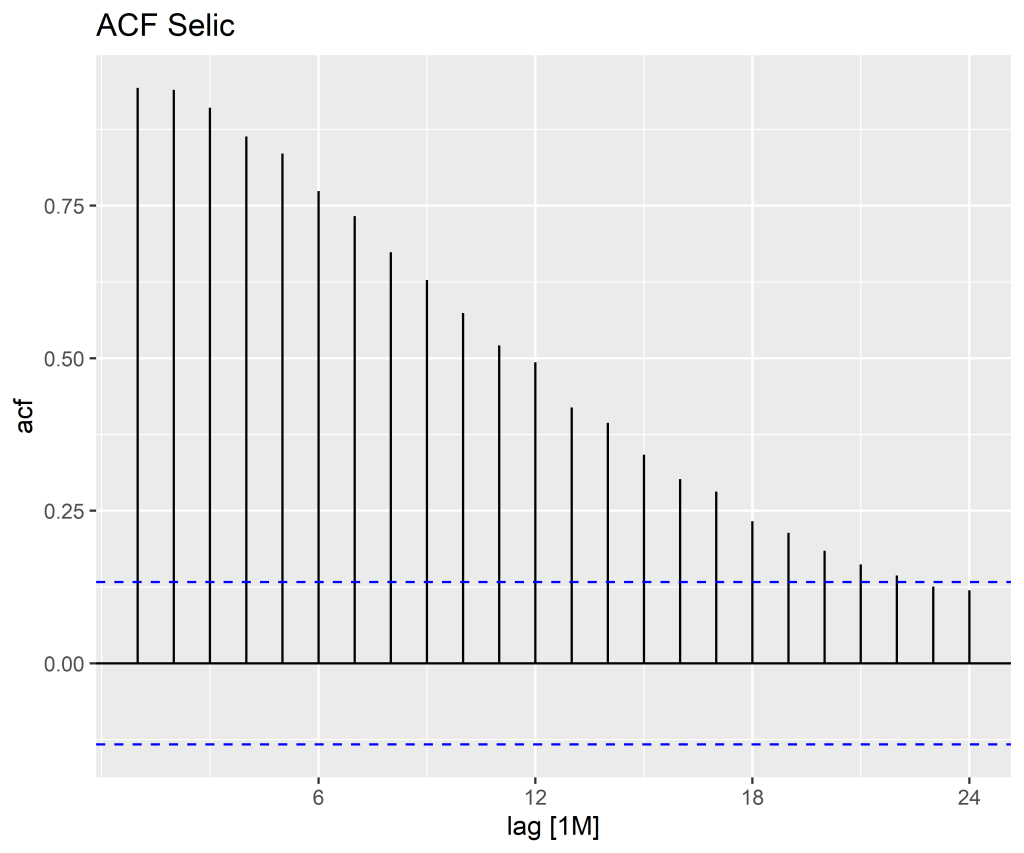
| lag | acf |
|---|---|
| 1M | 0.9429826 |
| 2M | 0.9397433 |
| 3M | 0.9103364 |
| 4M | 0.8633469 |
| 5M | 0.8356182 |
| 6M | 0.7738830 |
| 7M | 0.7328393 |
| 8M | 0.6739795 |
| 9M | 0.6280843 |
| 10M | 0.5741553 |
| 11M | 0.5207589 |
| 12M | 0.4936177 |
| 13M | 0.4191846 |
| 14M | 0.3943758 |
| 15M | 0.3419370 |
| 16M | 0.3020969 |
| 17M | 0.2812181 |
| 18M | 0.2327372 |
| 19M | 0.2138030 |
| 20M | 0.1846690 |
| 21M | 0.1620674 |
| 22M | 0.1437452 |
| 23M | 0.1257066 |
| 24M | 0.1196230 |
Código
Python
Código
array([ 1. , 0.58600222, 0.35399214, 0.21127288, 0.04306428,
-0.04123194, -0.01058157, 0.02373486, 0.0829602 , 0.1576327 ,
0.17736229, 0.17718907, 0.16163054, 0.0708879 , 0.01591198,
0.01971667, -0.10453837, -0.11966313, -0.15187464, -0.194883 ,
-0.14090267, -0.13621363, -0.10503274, -0.05900584, -0.01844174])Código
Código
sm.tsa.stattools.acf(tabela.selic.values, nlags = 24)
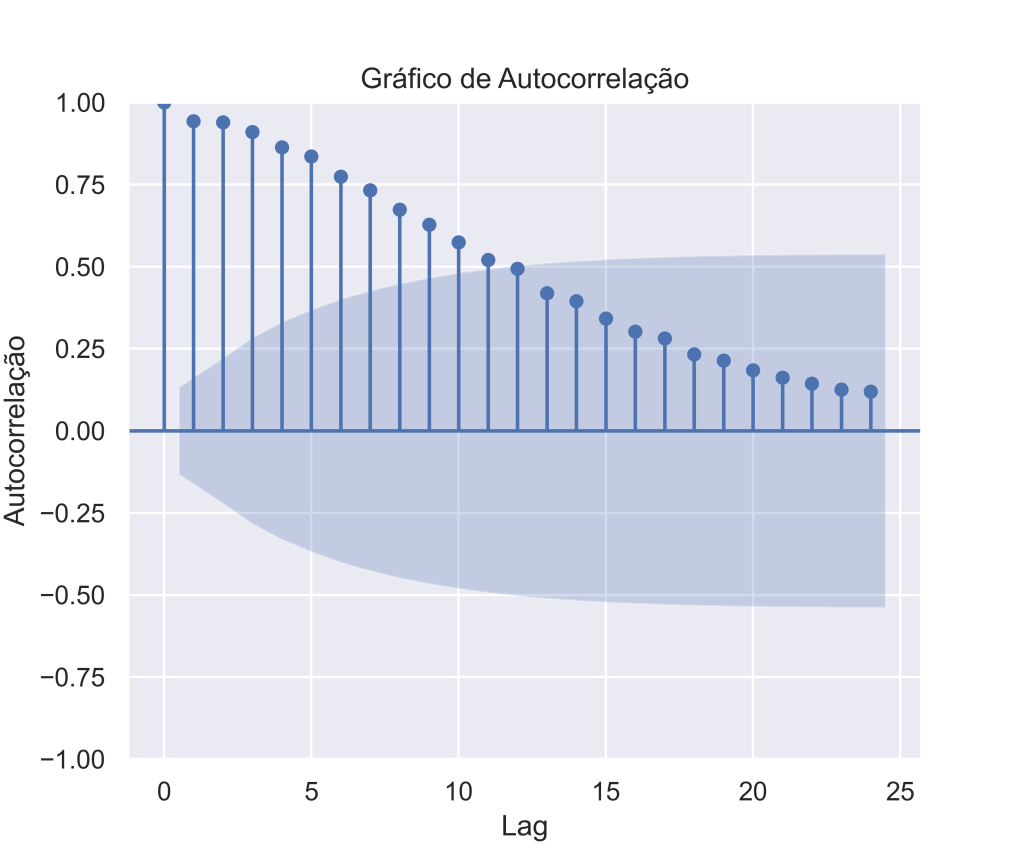
# Gráfico de autocorrelação selicarray([1. , 0.94298259, 0.93974331, 0.91033638, 0.86334691,
0.83561823, 0.77388297, 0.73283927, 0.67397952, 0.62808427,
0.57415532, 0.52075894, 0.49361772, 0.41918465, 0.39437582,
0.34193697, 0.30209692, 0.28121809, 0.23273716, 0.21380302,
0.18466905, 0.16206735, 0.14374523, 0.12570663, 0.11962301])Código
Vejam que a partir do cálculo do ACF, é possível criar uma visualização dos coeficientes estimados, e que são úteis para compreender a medida. Esse gráfico é conhecido como correlograma.
Nos gráficos acima, além dos coeficientes para cada defasagens, encontramos uma linha traçada ou um sombreado, indicando a significância estatística de que a correlação é diferente de zero.
Tendência e Sazonalidade
Quando os dados têm uma tendência, as autocorrelações para pequenas defasagens tendem a ser grandes e positivas porque as observações próximas no tempo também têm valores próximos. Portanto, o ACF de uma série temporal com tendência tende a ter valores positivos que diminuem lentamente à medida que as defasagens aumentam.
Quando os dados são sazonais, as autocorrelações serão maiores para as defasagebs sazonais (em múltiplos do período sazonal) do que para outros atrasos.
Quando os dados são de tendência e sazonais, existe uma combinação desses efeitos.
Nos casos acima, vemos uma forte tendência para Selic em que há um decaimento lento dos valores. Para o IPCA fica claro o padrão sazonal, visto que as defasagens próximas de 6 meses possuem valores de correlação próximos de 0 (ou mesmo negativos), enquanto para as defasagens próximas de 12 meses possuem uma correlação positiva.
Conclusão
Neste artigo, apresentamos o conceito de autocorrelação, avaliamos sua aplicabilidade no mundo real, verificamos como estimar e interpretar o coeficiente e, por fim, aplicamos a análise de autocorrelação com dados macro-financeiros do Brasil, usando as linguagens de programação R e Python.
Saiba mais
Se você se interessa por análise e ciência de dados e quiser adquirir os conhecimentos e habilidades destacados neste artigo, dê uma olhadinha nessa formação especial que a Análise Macro preparou:
E para obter os códigos completos deste exercício e de vários outros, dê uma olhada no Clube AM da Análise Macro, onde publicamos exercícios de ciência de dados toda semana em R e Python.
Referências
Forecasting: Principles and Practice Hyndman, R. & Athanasopoulos, G., 2021, 3rd ed. OTexts.

![Rendered by QuickLaTeX.com \[r_{k} = \frac{\sum\limits_{t=k+1}^T (y_{t}-\bar{y})(y_{t-k}-\bar{y})} {\sum\limits_{t=1}^T (y_{t}-\bar{y})^2},\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-d74b312f8289ecb4271865dab8b727c5_l3.png)