Propriedades estatísticas de séries temporais

Série temporal é uma estrutura de dados fundamental para as áreas de economia e finanças, uma vez que a maioria das variáveis nessas áreas são observadas ao longo do tempo. Compreender as principais características estatísticas de uma série temporal é essencial para aqueles interessados em analisar dados econômicos.

O que é uma Série Temporal?

Dados de séries temporais (time series, no inglês) são estruturas de dados tabulares compostos de observações indexadas no tempo, frequentemente constituindo observações sequenciais e igualmente espaçadas entre períodos diferentes. A frequência de dados podem ser dispostas a hora, dia, semana, mensal, trimestral ou anual.

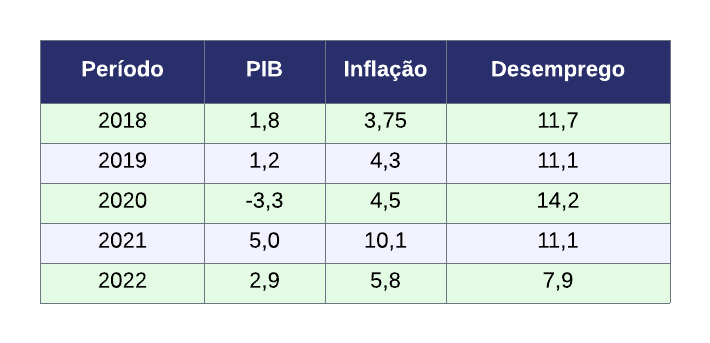
Diferente de dados de corte transversal (cross section, no inglês) são estruturas de dados tabulares que são coletados em apenas um período no tempo, podendo ser sobre diversas observações (como pessoas, empresas, países, etc.), dados com séries temporais, em linhas gerais, possuem um formato parecido com esse abaixo:

É uma estrutura de dados muito utilizada em diversas áreas como estatística, econometria, clima, finanças, macroeconomia e outras. A análise e a previsão de séries temporais são as aplicações mais comuns com essa estrutura de dados.

Para o nosso interesse, há diversos conjuntos de dados econômicos que se apresentam como uma série temporal, tais como:

Taxa de desemprego;
Juros básicos de uma economia;
Produto Interno Bruto (PIB);
Taxa de inflação.

Visualização

Uma série temporal pode ser facilmente visualizada em um gráfico, em que:

eixo x representa o tempo (indexação);
eixo y representa os valores da série.

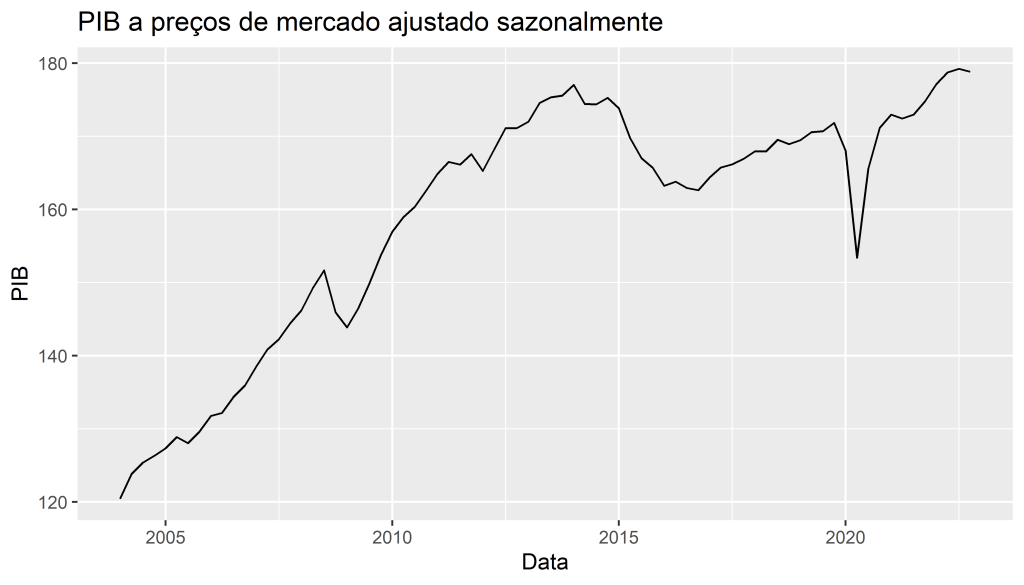
Verificamos abaixo a série temporal do PIB trimestral a preços de mercado ajustado sazonalmente. Cada valor no eixo x representa o trimestre, e no eixo y, há o valor correspondente verificado no período.

Para obter todo o código do processo de criação dos gráficos e das propriedades das séries utilizando o R e o Python como ferramenta, faça parte do Clube AM, o repositório de códigos da Análise Macro, contendo exercícios semanais.

O campo de estudo referente às propriedades e relação dessas variáveis econômicas chama-se econometria de séries temporais.

A econometria de séries temporais estará, nesse contexto, preocupada em explicar o passado de uma determinada variável, construir relações entre variáveis distintas e gerar previsões para alguns períodos à frente. Para isso, devemos construir modelos, simplificações da realidade que buscam ressaltar algumas características importantes das séries em que estamos interessados.

Objetivos da análise de séries temporais

Conforme Morettin (2006), se temos em mãos uma série temporal $Y(t_1), \dotsc, Y(t_n)$

, observada nos instantes $t_1, \dotsc, t_n$

, estamos interessados em:

Investigar o mecanismo gerador da série temporal;
Descrever o comportamento passado da série, por meio de suas propriedades estatísticas e gráficos;
Fazer previsões de valores futuros da série.

Para descrever as séries, modelos probabilísticos ou modelos estocásticos são construídos, e que no qual devem ser simples e parcimoniosos, isto é, devem ser fáceis de serem manipulados e devem possuir o menor número de parâmetros possível.

Séries Temporais, Processos Estocásticos e o Processo gerador de dados

Um processo aleatório ou estocástico é uma coleção de variáveis aleatórias ordenadas no tempo.

Por exemplo, se temos a série do PIB trimestral, como definimos ela como um processo estocástico? Basicamente, o valor do PIB em determinado trimestre pode ser qualquer um, a depender do clima econômico e político, portanto, se tivermos um valor $Y$ qualquer do PIB no período, temos uma realização particular de todas as possibilidades do processo, ou seja, se tivermos o histórico de 1950 até 2023 para o Brasil, temos as realizações particulares do processo, e portanto, uma amostra.

Do mesmo modo que utilizamos as amostras de dados para extrair inferências sobre a população, utilizamos, em séries temporais, a realização para extrair inferências sobre o processo estocástico subjacente.

Sendo um pouco mais formal, temos a definição de Morettin (2006):

Seja $T$ um conjunto arbitrário. Um processo estocástico é uma família $Y = \{ Y(t), t \in T \}$ , tal que, para cada $t \in T$ , $Z(t)$ é uma variável aleatória.

Nestas condições, um processo estocástico é uma família de variáveis aleatórias (v.a.), que supomos definidas em um mesmo espaço de probabilidades, e que é representada por:

$\begin{equation*} \left \{ Y \right \}_{t=1}^{T} = \left \{ y_{1}, y_{2}, ..., y_{t}, ..., y_{T-1}, y_{T} \right \} \end{equation*}$

Nesses termos, esse processo estocástico desconhecido é o que chamamos de processo gerador dos dados que formam uma série temporal. O desafio do econometrista será, portanto, tendo acesso apenas à série temporal, buscar compreender esse processo estocástico desconhecido. Quanto melhor for essa compreensão, melhor será a modelagem e, com efeito, a previsão de observações futuras.

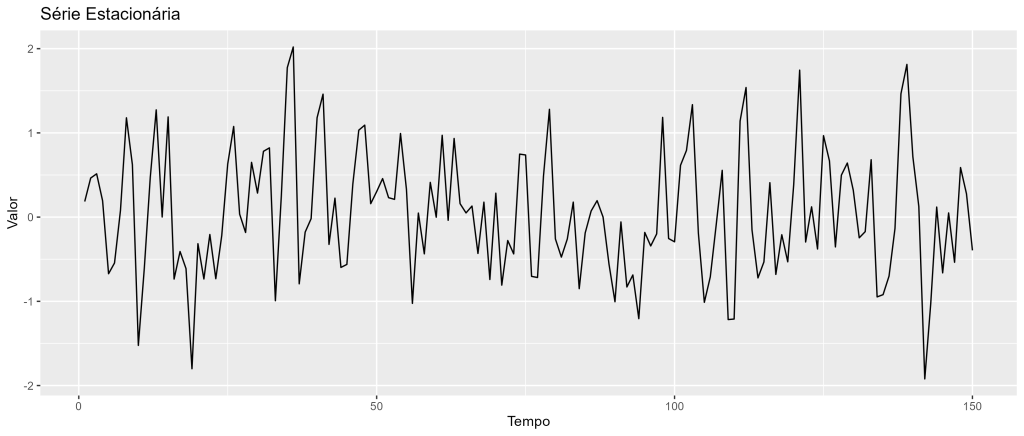
Estacionariedade (processo estocástico estacionário)

Um tipo de processo estocástico que merece grande atenção é o assim chamado processo estocástico estacionário.

Como vimos acima, uma série temporal nada mais é do que a realização particular de um processo estocástico. Essa realização, contudo, pode ser estacionária ou não. Observe, por exemplo, a série abaixo.

Tal série temporal tenderá a retornar para a sua média (o que chamamos de reversão da média), e flutuações em torno dessa média (mensurada por sua variância) terão, de modo geral, uma amplitude constante. Em outras palavras, essa série (que é estacionária) não se desviará muito de seu valor médio em virtude da variância finita.

E caso não tenhamos uma série com o comportamento acima? Vejamos a série abaixo.

Ao olhar a série acima, chama atenção a tendência da mesma. Significa dizer que se estivéssemos interessados em modelar a série, teríamos de levar essa tendência crescente em consideração. Isso é, de fato, um problema.

Então, como definimos uma série estacionária? Um processo estocástico será chamado de estacionário se sua média e variância forem constantes ao longo do tempo e o valor da covariância entre os dois períodos de tempo depender apenas da distância, do intervalo ou da defasagem entre os dois períodos e não o tempo real ao qual a covariância é computada.

Para explicar a estacionariedade fraca, considere o $Yt$

como uma série temporal estocástica com essas propriedades:

$\text{Média:} = E(y_{t}) = E(t-k) = \mu$

$\text{Variância:} E\left [(y_{t} - \mu)^2 \right ] = E\left [(y_{t-k} - \mu)^2 \right ] = \sigma_{y}^2$

$\text{Covariância:} E\left [(y_{t} - \mu)(y_{t-k} - \mu) \right ] = E\left [(y_{t-j} - \mu)(y_{t-j-k} - \mu) \right ] = \gamma_{k}$

onde $\mu$

, $\sigma_{y}^2$

e $\gamma_{k}$

são todas constantes.

A estacionariedade é extremamente importante para a modelagem de uma série temporal. Isso porque, suponha que estejamos regredindo $\left \{ y \right \}_{t=1}^{T}$

contra $\left \{ x \right \}_{t=1}^{T}$

. Se estivermos lidando com séries não estacionárias, isso implica que os coeficientes que encontrarmos não serão representativos da relação entre elas. Estaremos, assim, encontrando uma relação espúria. Logo, antes de construir um modelo econométrico, precisaremos nos certificar se as séries em questão são, de fato, estacionárias ou, claro, lidar com esse fato através de algum outro procedimento, como veremos mais à frente nesse curso.

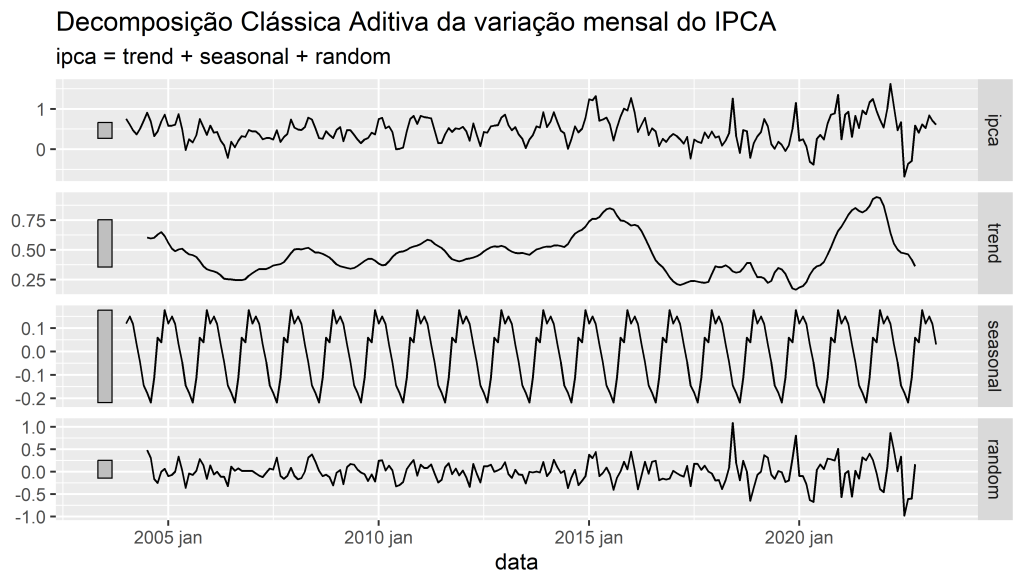
Decomposição de uma série temporal

De modo a compreender o processo gerador de dados de uma determinada série temporal, pode ser interessante decompô-la em alguns componentes, como abaixo:

$\begin{equation*}y_{t} = S_{t} + T_{t} + R_t \end{equation*}$

Onde, no tempo $t$

, $y_{t}$

é uma série temporal, $T_{t}$

é uma tendência, $S_{t}$

é um efeito sazonal e $R_t$

é um termo de erro.

Alternativamente, temos a decomposição multiplicativa:

$\begin{equation*}y_{t} = S_{t} \times T_{t} \times R_t \end{equation*}$

A decomposição aditiva é a mais adequada se a magnitude das flutuações sazonais, ou a variação em torno do ciclo de tendência, não varia com o nível da série temporal.

Quando a variação no padrão sazonal, ou a variação em torno do ciclo de tendência, parece ser proporcional ao nível da série temporal, então uma decomposição multiplicativa é mais apropriada. Decomposições multiplicativas são comuns em séries temporais econômicas.

Componentes

Tendência

Uma tendência existe quando há um aumento ou diminuição de longo prazo nos dados. Não precisa ser linear. Às vezes, nos referiremos a uma tendência como "mudança de direção", quando ela pode passar de uma tendência crescente para uma tendência decrescente.

Sazonalidade

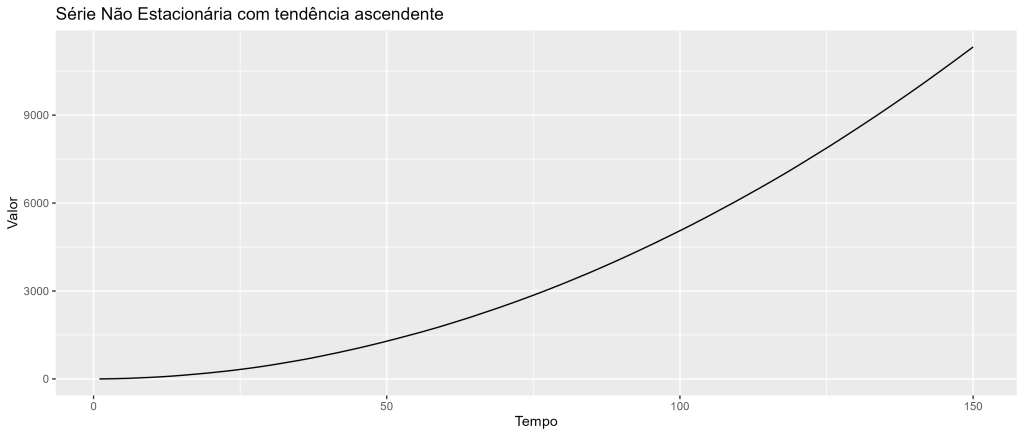
Um padrão sazonal ocorre quando uma série temporal é afetada por fatores sazonais, como a época do ano ou o dia da semana. A sazonalidade é sempre de um período fixo e conhecido.

Ciclo e o Termo de erro

Um ciclo ocorre quando os dados exibem aumentos e quedas que não são de uma frequência fixa. Essas flutuações geralmente são devidas a condições econômicas e geralmente estão relacionadas ao "ciclo de negócios". A duração dessas flutuações é geralmente de pelo menos 2 anos.

Quando decompomos uma série temporal em componentes, geralmente combinamos a tendência e o ciclo em um único componente de ciclo de tendência (geralmente chamado apenas de tendência para simplificar).

Assim, podemos pensar em uma série temporal como compreendendo três componentes: um componente de ciclo de tendência, um componente sazonal e um componente restante/termo de erro (contendo qualquer outra coisa na série temporal).

Pontos importantes:

Para algumas séries temporais (por exemplo, aquelas que são observadas pelo menos diariamente), pode haver mais de um componente sazonal, correspondendo aos diferentes períodos sazonais.

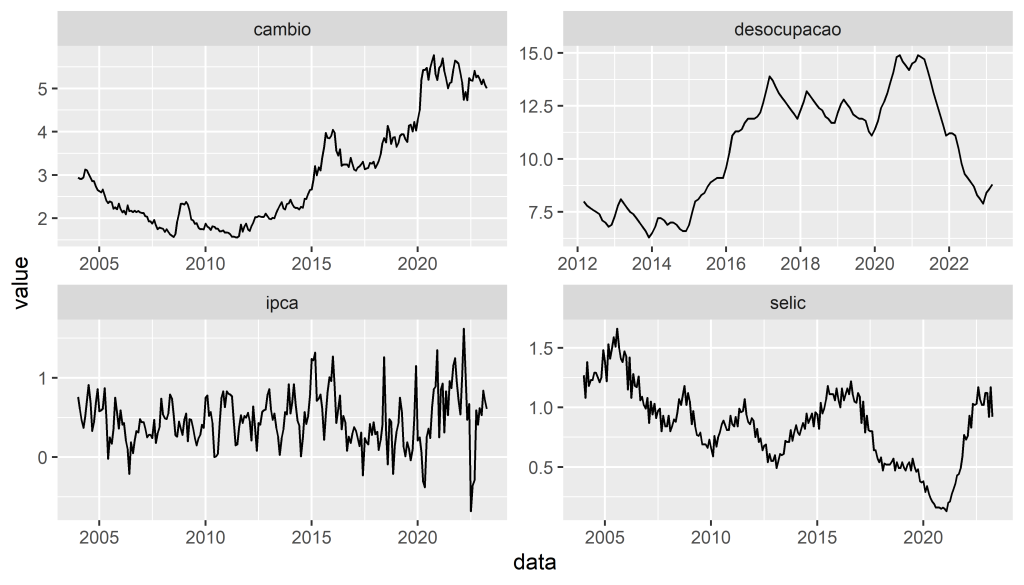
Exemplo de séries temporais econômicas

Vejamos as diferentes séries temporais, referentes a variáveis econômicas do Brasil. Quais apresentam tendências, sazonalidades e os ciclos?

Os gráficos mostram de forma bem clara fortes tendências nas séries da taxa de câmbio, taxa de desocupação e taxa SELIC, ainda que com certa irregularidade, enquanto que a série da inflação medida pelo IPCA possui aspecto parecido de uma série estacionária.

Decomposição

É possível decompor os componentes de uma série temporal através de diferente métodos. Abaixo, utilizamos o que é conhecido como decomposição clássica (aditiva) para verificar a tendência, a sazonalidade e o termo de erro da série da variação mensal do IPCA.

Identificar corretamente esses componentes é um passo importante para compreender o processo gerador de dados de uma série.

Tipos de modelos de séries temporais

Há, basicamente, duas formas de se entender uma série temporal, do ponto de vista econométrico. Modelos de série temporal podem ser:

Modelos Univariados - as características da série de interesse são explicadas exclusivamente a partir do comportamento da própria série;
Modelos Multivariados - as características da série de interesse são explicadas não apenas em função da própria série, mas também por outras séries.

Obs: Os modelos multivariados podem ser escalares, quando há apenas uma única equação, ou vetoriais, quando há múltiplas equações.

_____________________________________
Quer aprender mais?

Seja um aluno da nossa trilha de Macroeconomia Aplicada e aprenda a criar projetos voltados para a Macroeconomia.

________________________________________________

Referências

Enders, W. 2009. Applied Econometric Times Series. Wiley Series in Probability and Statistics. Wiley.

Hyndman, R.J., & Athanasopoulos, G. (2021) Forecasting: principles and practice, 3rd edition, OTexts: Melbourne, Australia. OTexts.com/fpp3.

Morettin, Pedro A., and Clélia Toloi. 2006. Análise de séries temporais. Editora Blucher.

Pfaff, B. 2008. Analysis of Integrated and Cointegrated Time Series with R. Second. New York: Springer.

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Criando seu primeiro Transformer para previsão de séries econômicas

Como avaliar modelos de IA na previsão macroeconômica?

Análise exploratória e seleção de séries temporais econômicas para modelagem

Transformers para Análise de Séries Temporais

O que é e como funciona a Arquitetura Transformer

Tratamento e transformação de séries temporais macroeconômicas para modelagem

Outros artigos relacionados

Criando seu primeiro Transformer para previsão de séries econômicas

Este tutorial mostra como construir e avaliar um modelo Transformer para prever a Dívida Bruta do Governo Geral (DBGG) do Brasil. Utilizando a biblioteca darts, exploramos desde a coleta dos dados via API do Banco Central até a comparação com modelos clássicos, como ETS e Theta.

Como avaliar modelos de IA na previsão macroeconômica?

Descubra como economistas e cientistas de dados estão combinando econometria e inteligência artificial para aprimorar previsões macroeconômicas. Neste post, você vai entender as principais etapas de avaliação de modelos — da preparação dos dados à validação cruzada — e conhecer as métricas e técnicas que revelam quais métodos realmente entregam as melhores previsões. Uma leitura essencial para quem quer compreender o futuro da análise econômica orientada por dados.

Análise exploratória e seleção de séries temporais econômicas para modelagem

Quer entender como transformar dados econômicos brutos em previsões macroeconômicas precisas? Neste post, mostramos passo a passo como realizar a análise exploratória e seleção de séries temporais com Python — desde o tratamento de dados e remoção de multicolinearidade até a escolha das variáveis mais relevantes usando técnicas de machine learning e econometria. Um guia essencial para quem quer unir teoria econômica e inteligência artificial na prática da previsão macroeconômica.

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!

Propriedades estatísticas de séries temporais

O que é uma Série Temporal?

Visualização

Objetivos da análise de séries temporais

Séries Temporais, Processos Estocásticos e o Processo gerador de dados

Estacionariedade (processo estocástico estacionário)

Decomposição de uma série temporal

Componentes

Tendência

Sazonalidade

Ciclo e o Termo de erro

Pontos importantes:

Exemplo de séries temporais econômicas

Decomposição

Tipos de modelos de séries temporais

_____________________________________ Quer aprender mais?

Referências

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Outros artigos relacionados

Boletim AM

Boletim AM

_____________________________________
Quer aprender mais?