Como realizar uma análise de dados da ação de sua carteira? Uma das formas mais eficientes de compreender os movimentos do preço de uma ação é através de sua volatilidade. Para tanto, criamos uma análise da volatilidade usando Python, tomando como exemplos os retornos mensais da ação da WEGE3.
Ao analisar ativos financeiros, usualmente, utiliza-se o retorno de seu preço. O retorno de uma ação é uma medida de desempenho que representa o ganho ou a perda de um investimento em um determinado período.
Para obter todo o código em R e Python para os exemplos abaixo, faça parte do Clube AM, o repositório de códigos da Análise Macro, contendo exercícios semanais.
É calculado como a variação percentual no preço da ação, ajustada por dividendos e outras distribuições.
Fórmula do Retorno:
Onde:
- é o retorno no tempo
- é o preço da ação no tempo
- é o preço da ação no tempo
O Retorno é utilizado pelos seguintes motivos:
- Medida Direta de Desempenho: O retorno proporciona uma medida direta e quantitativa do desempenho de uma ação, permitindo que os investidores comparem o rendimento de diferentes ações ou portfólios de forma objetiva.
- Comparabilidade: Ao expressar o desempenho como uma porcentagem, os retornos permitem a comparação entre diferentes ativos financeiros, independentemente dos seus preços absolutos.
- Análise de Risco e Retorno: Investidores utilizam o retorno para avaliar a relação entre risco e retorno. Eles procuram maximizar o retorno esperado para um dado nível de risco.
O Retorno permite realizar a avaliação da Volatilidade do preço de uma ação. A Volatilidade é uma medida da variação dos retornos de um ativo ao longo do tempo. Ela quantifica a dispersão ou a variabilidade dos retornos em relação à média.
A Volatilidade auxilia na avaliação de uma ação, por que representa os seguintes fatores:
- Medida de Risco: A volatilidade é uma medida crucial do risco de um ativo. Alta volatilidade indica alta incerteza nos retornos, o que é um sinal de risco maior.
- Tomada de Decisões: Investidores utilizam a volatilidade para tomar decisões informadas sobre suas carteiras. Um ativo com alta volatilidade pode ser evitado por investidores avessos ao risco.
- Diversificação: A análise da volatilidade de diferentes ativos permite que investidores criem carteiras diversificadas que minimizam o risco total, aproveitando a correlação entre os ativos.
Existem diversas formas de avaliar a volatilidade de uma ação. Usualmente utiliza-se medidas do momentos da distribuição dos retornos, como o desvio padrão, assimetria e curtose. Veremos como calcular esses valores usando o Python. Outra forma é através de Modelos, tal como o Modelo de Mercado ou CAPM, que permitem obter uma medida de volatilidade de mercado, o Beta.
Como analisar a Volatilidade de Ações usando Python?
Os resultados obtidos abaixo seguem as seguintes etapas:
- Coleta dos preços mensais de fechamentos da ação WEGE3 e Ibovespa, no período de 01/01/2010 até 31/12/2023.
- Cálculo dos retornos mensais
- Análise Exploratória de dados: Histograma e Estatísticas Descritivas
- Análise da Volatilidade:
- Desvio Padrão Anualizado Móvel
- Assimetria Móvel
- Curtose Móvel
- Beta Móvel
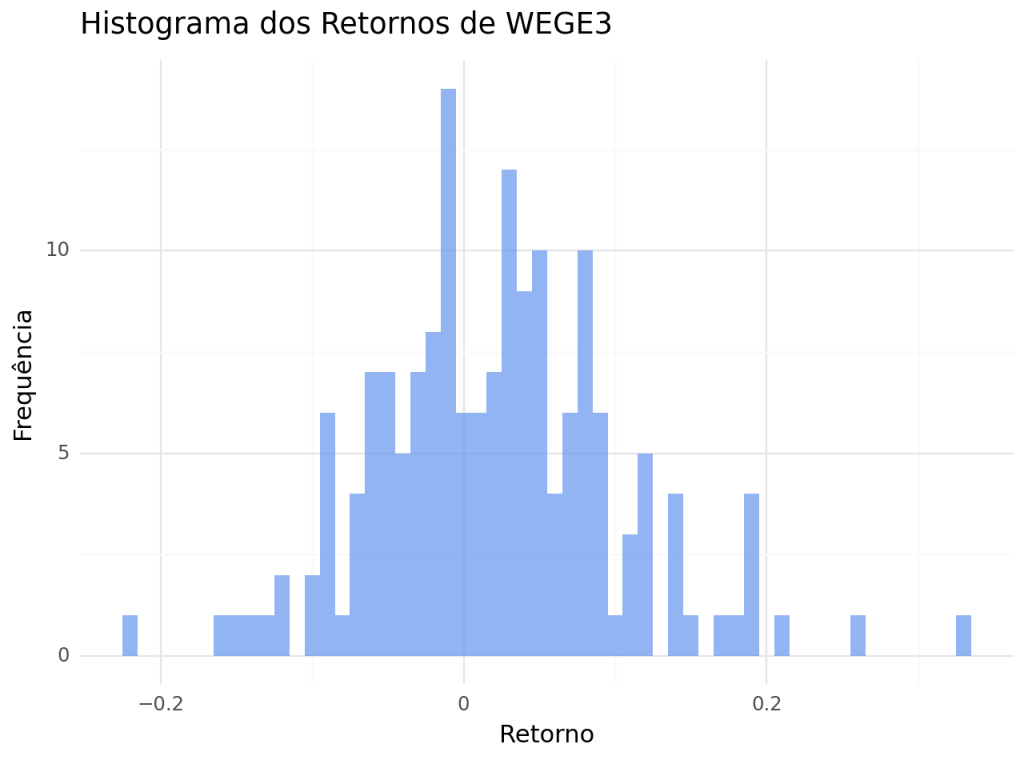
Histograma
Na avaliação de retornos, um histograma pode ser usado para visualizar como os retornos de um ativo estão distribuídos ao longo do tempo. Usualmente, a distribuição de retornos de ativos financeiros possuem valores extremos, representado nas caudas, como é o caso abaixo.
Estatística Descritiva
Abaixo, as estatísticas descritivas da amostra dos retornos da WEGE3.
Código
| Retorno | |
|---|---|
| count | 167.000000 |
| mean | 0.020662 |
| std | 0.080917 |
| min | -0.219387 |
| 25% | -0.033595 |
| 50% | 0.022182 |
| 75% | 0.070482 |
| max | 0.331783 |
| Assimetria | 0.432445 |
| Curtose | 1.222026 |
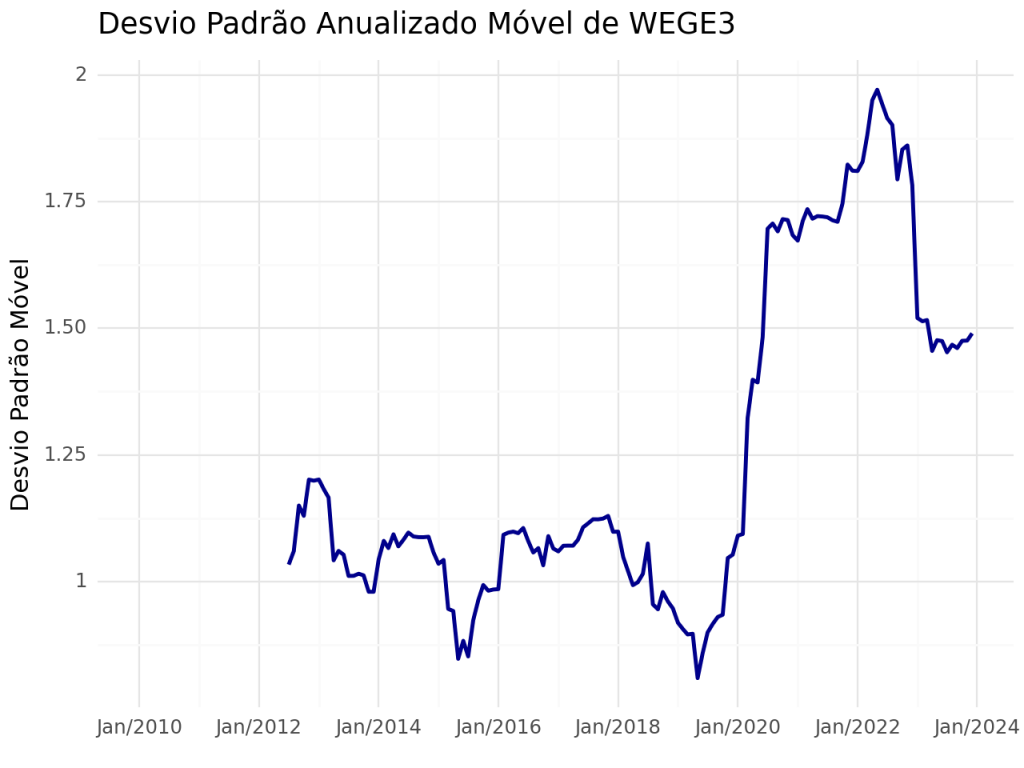
Desvio Padrão Móvel
O desvio padrão móvel é uma medida estatística que calcula a volatilidade de uma série temporal de retornos ao longo de um período de tempo móvel.
É utilizado para identificar como a volatilidade de um ativo financeiro muda ao longo do tempo. Assim como o desvio padrão tradicional, ele quantifica a dispersão dos retornos em relação à média, mas faz isso de forma dinâmica, ajustando-se continuamente à medida que novos dados são adicionados e os mais antigos são descartados.
Quanto maior o valor, mais volátil o ativo é.
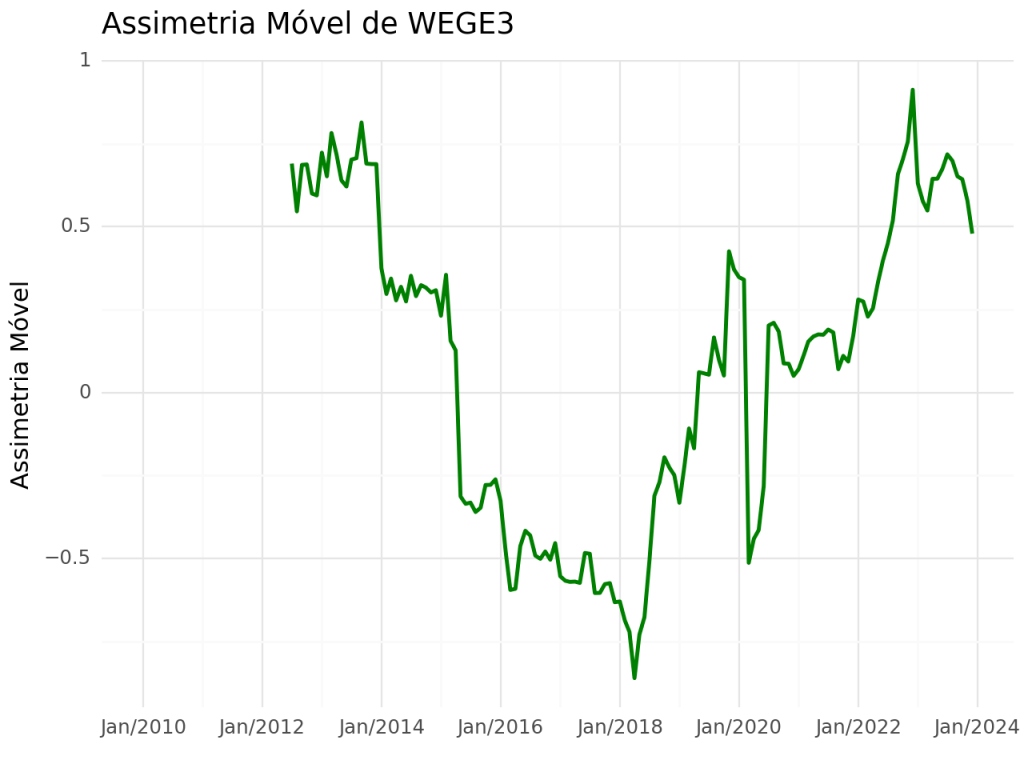
Assimetria Móvel
A assimetria é uma medida de simetria na distribuição dos retornos de um ativo financeiro. Ela indica o grau de distorção ou desvio da curva de distribuição em relação a uma distribuição normal (simétrica). Uma distribuição simétrica tem assimetria zero. Uma distribuição com cauda longa à direita (positivamente assimétrica) tem uma assimetria positiva, enquanto uma distribuição com cauda longa à esquerda (negativamente assimétrica) tem uma assimetria negativa.
Se a assimetria móvel é positiva, indica que há uma tendência para retornos maiores do que a média, com uma cauda mais longa à direita.
Se a assimetria móvel é negativa, indica que há uma tendência para retornos menores do que a média, com uma cauda mais longa à esquerda.
Se a assimetria móvel é próxima de zero, sugere que os retornos estão aproximadamente simetricamente distribuídos ao redor da média.
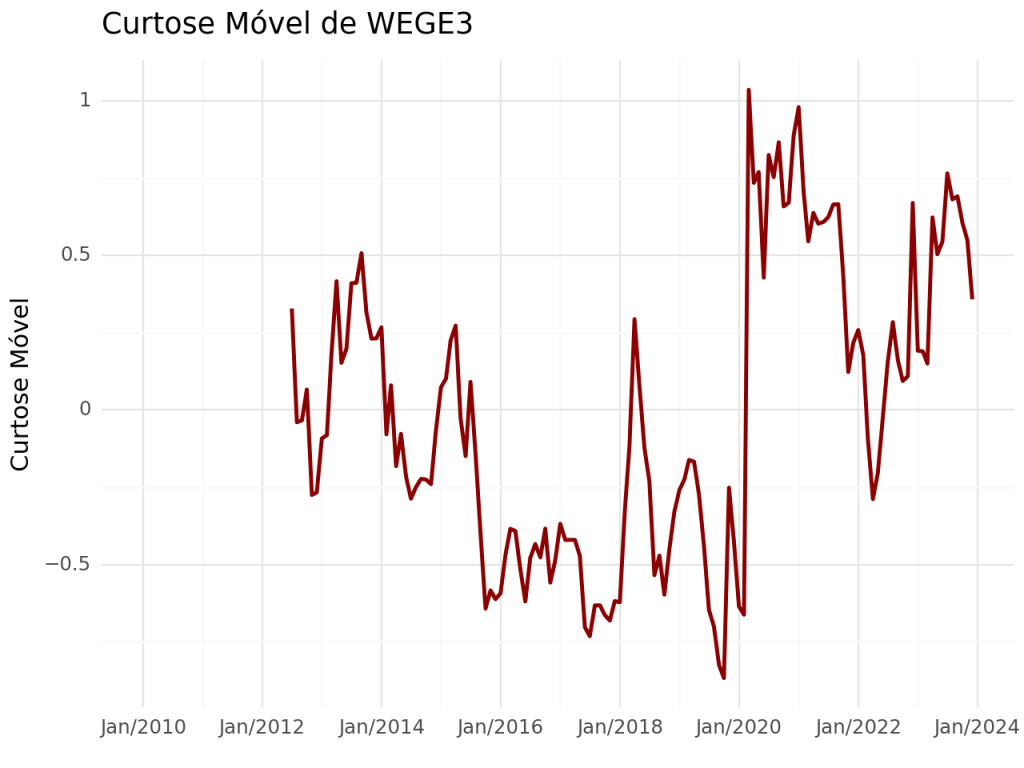
Curtose Móvel
Curtose é uma medida estatística que descreve a forma das caudas de uma distribuição em relação a uma distribuição normal. Especificamente, a curtose indica a presença de extremos ou outliers.
Um valor alto da Curtose representa uma distribuição com caudas mais pesadas e pontas mais altas do que a normal, sugerindo uma maior probabilidade de eventos extremos. O contrário para um valor baixo de Curtose.
Para Curtose para valores próximos de 0, indica uma distribuição aproximadamente normal.
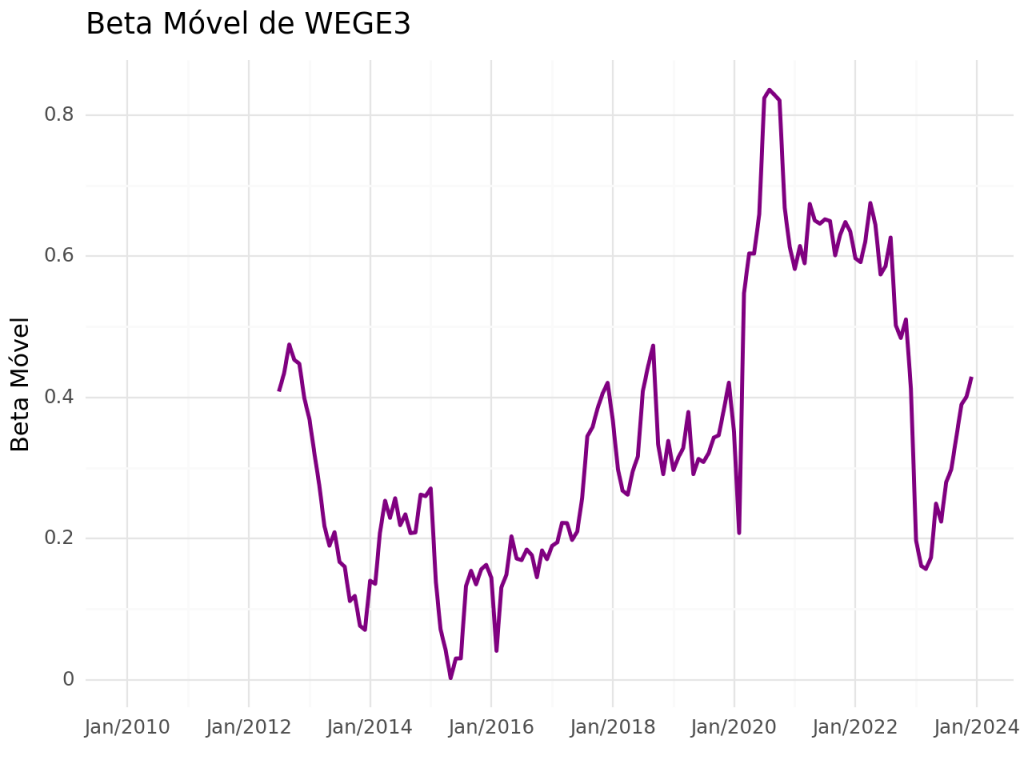
Beta Móvel
O beta é uma medida da sensibilidade do retorno de um ativo em relação ao retorno de um índice de referência, geralmente um índice de mercado como o Ibovespa. O beta indica o risco sistemático ou de mercado do ativo, em comparação com o mercado como um todo.
- Beta = 1: O ativo move-se em consonância com o mercado.
- Beta > 1: O ativo é mais volátil que o mercado.
- Beta < 1: O ativo é menos volátil que o mercado.
_____________________________________
Quer aprender mais?
Clique aqui para fazer seu cadastro no Boletim AM e baixar o código que produziu este exercício, além de receber novos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas diretamente em seu e-mail.