Uma importante medida em finanças é o risco associado a um ativo e a volatilidade de ativos é talvez a medida de risco mais utilizada. Há, entretanto, diversas medidas de volatilidade.
Como a média móvel ponderada exponencialmente (EWMA), a heteroscedasticidade condicional autorregressiva (ARCH) e a heteroscedasticidade condicional autorregressiva generalizada (GARCH). A característica marcante dos modelos é que eles reconhecem que as volatilidades e correlações não são constantes. Durante alguns períodos, uma determinada volatilidade ou correlação pode ser relativamente baixa, enquanto durante outros pode ser relativamente alta. Os modelos tentam acompanhar as variações da volatilidade ou da correlação com o tempo.
Características da Volatilidade
Ainda que a volatilidade seja bem definida, ela não é diretamente observada na prática. Nós observamos os preços dos ativos e seus derivativos. A volatilidade deve ser, então, estimada com base nesses preços observados. Ainda, ela apresenta algumas características comuns associadas aos retornos dos ativos. Listamos abaixo algumas delas:
- A volatilidade é alta em certos períodos e baixa em outros, configurando o que a literatura chama de volatility clusters;
- A volatilidade evolui de maneira contínua, de modo que saltos não são comuns;
- A volatilidade costuma variar em um intervalo fixo;
- A volatilidade costuma reagir de forma diferente a um aumento muito grande nos preços e a um decréscimo igualmente muito grande, com o último representando maior impacto.
Essas características implicam que, de modo geral, a volatilidade é uma série estacionária. Ademais, essas características determinam a forma como os modelos serão construídos.
De fato, alguns modelos de volatilidade são formatados justamente para corrigir a inabilidade dos atualmente existentes em capturar algumas das características mencionadas acima.
Modelos de Volatilidade
O desvio padrão, uma métrica simples e amplamente adotada para medir a dispersão dos retornos em relação à média, tem suas limitações ao assumir uma distribuição normal dos retornos e ignorar correlações entre períodos. Essa abordagem simplificada não consegue capturar as nuances complexas da volatilidade financeira.
Essa lacuna é evidente devido à presença de heteroscedasticidade condicional nos retornos. A heteroscedasticidade condicional é uma característica comum em séries temporais financeiras, indicando que a volatilidade dos retornos frequentemente manifesta mudanças sistemáticas ao longo do tempo.
A heteroscedasticidade condicional refere-se à presença de volatilidade condicional variável ao longo do tempo em uma série temporal. Em outras palavras, a heteroscedasticidade condicional ocorre quando a variância dos erros de uma série depende das informações disponíveis no tempo anterior.
Por exemplo, nos mercados financeiros, pode-se observar períodos de alta volatilidade seguidos por períodos de baixa volatilidade. Esses padrões na volatilidade são fundamentais para a modelagem e previsão de riscos financeiros.
Os modelos ARCH e GARCH são mais adequados quando se deseja modelar e prever a volatilidade condicional dos retornos, levando em consideração a autocorrelação e a heteroscedasticidade.
Análise da Volatilidade do Índice Bovespa
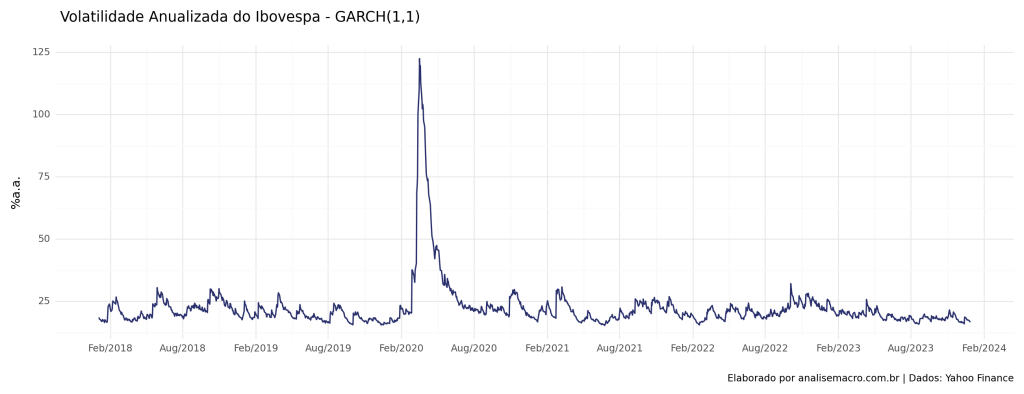
Com base no modelo GARCH(1,1), iremos realizar a modelagem da variância condicional dos log retornos diários do Ibovespa, abrangendo o período de janeiro de 2018 até dezembro de 2023. O objetivo principal é compreender a implementação desse modelo utilizando a linguagem de programação Python, além de conduzir uma análise do mercado acionário brasileiro ao longo do período amostral.
Ao concluirmos este exercício, teremos a capacidade de obter uma medida representativa da variância de longo prazo da série temporal. Essa medida poderá ser comparada com a variância histórica, permitindo-nos inferir se a volatilidade presente está atualmente inferior ou superior àquela projetada para o futuro. Essa análise contribuirá para uma melhor compreensão da dinâmica da volatilidade no mercado acionário brasileiro.
Para obter o código deste exercício faça parte do Clube AM e receba toda semana os códigos em R/Python, vídeos, tutoriais e suporte completo para dúvidas.
Estrutura do Modelo do GARCH
Seja o logaritmo do retorno de um ativo no índice de tempo
. A ideia básica por trás do estudo de volatilidade é que a série
é ou seriamente não correlacionada ou possui correlações seriais de ordem inferior, mas é uma série dependente
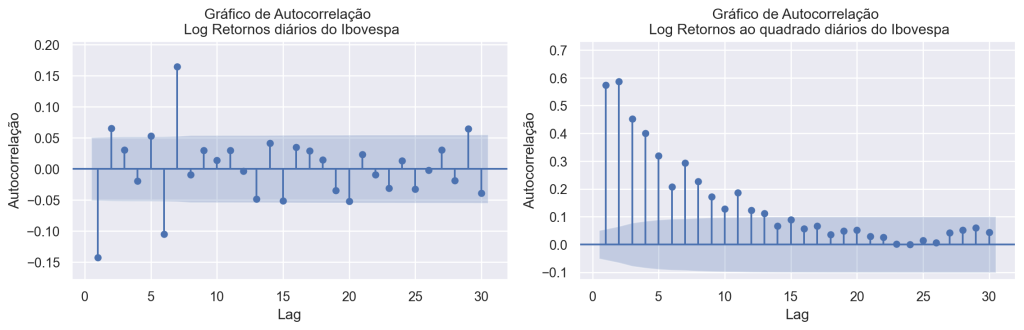
Na figura abaixo, apresenta-se a Função de Autocorrelação Amostral (FAC) da série de retornos logarítmicos, sugerindo algumas correlações seriais significativas (em geral, não há correlação serial). Mostra também a FAC amostral dos retornos logarítmicos ao quadrado . Esses dois gráficos sugerem claramente que os retornos logarítmicos diários não são serialmente independentes. Modelos de volatilidade tentam capturar essa dependência na série de retornos.
De modo a colocar os modelos de volatilidade em uma perspectiva apropriada, é informativo considerar a média e a variância condicionais de dado
, isto é,
onde é o conjunto de informação disponível no período
. Tipicamente,
consiste em todas as funções lineares dos retornos passados. Ou seja, queremos realizar previsões em
do retorno futuro e seus momentos utilizando a informação disponível até o tempo
.
De modo a construir nosso modelo de volatilidade, a equação para deveria ser simples, de modo que nós assumimos que
segue uma média zero, uma média constante ou um modelo de série temporal simples tal qual um modelo
.
Assim, dado que , temos que
será dado por
será referido como um choque ou inovação do retorno de um ativo no período
ou mesmo erro de previsão.
Sendo assim, temos que a variância será
O modelo para é referido como equação da média para
e o modelo para
é a equação de volatilidade para
.
Construção do modelo
Construir um modelo de volatilidade para uma série de retorno de ativo consiste em quatro etapas:
- Especificar uma equação da média testando para dependência serial nos dados e, se necessário, construir um modelo econométrico para a série de retorno de modo a remover qualquer dependência linear;
- Utilizar os resíduos da equação da média para testar efeitos ARCH;
- Especificar um modelo de volatilidade se o efeito ARCH foi estatisticamente significativo e performar uma estimativa conjunta da equação da média e da volatilidade;
- Checar o modelo estimado com cuidado e refinar, caso necessário.
Modelo GARCH
O Modelo GARCH foi proposto por Bollerslev (1986), como uma versão melhorada do modelo ARCH produzido por Engle (1982). Definimos
onde é uma variável aleatória IID.
Podemos utilizar a distribuição Normal, t-Student, t-student assimétrica, etc.
é o processo da variância e possui componente autoregressiva e
dependência de .
Aqui, representa
, onde
é o peso alocado a taxa de variância de longo prazo
,
é o peso alocado a
e
é peso alocado a
Depois que ,
e
foram estimados, podemos calcular
como
. A variância de longo prazo VL pode então ser calculada como
. Para um processo GARCH(1,1) estável, precisamos que
. Caso contrário, o peso aplicado à variância de longo prazo é negativo.
Abaixo, estimamos o GARCH(1,1) para a série de log retornos diários do Ibovespa, tomando como equação da média um AR(1), e uma distribuição t de student assimétrica.
Código
| Dep. Variable: | Adj Close | R-squared: | 0.000 |
| Mean Model: | AR | Adj. R-squared: | 0.000 |
| Vol Model: | GARCH | Log-Likelihood: | -2530.89 |
| Distribution: | Standardized Skew Student's t | AIC: | 5073.78 |
| Method: | Maximum Likelihood | BIC: | 5105.60 |
| No. Observations: | 1485 | ||
| Date: | Mon, Jan 08 2024 | Df Residuals: | 1484 |
| Time: | 16:38:23 | Df Model: | 1 |
| coef | std err | t | P>|t| | 95.0% Conf. Int. | |
| Const | 0.0656 | 3.212e-02 | 2.043 | 4.110e-02 | [2.653e-03, 0.129] |
| coef | std err | t | P>|t| | 95.0% Conf. Int. | |
| omega | 0.0842 | 2.773e-02 | 3.038 | 2.379e-03 | [2.990e-02, 0.139] |
| alpha[1] | 0.0767 | 1.728e-02 | 4.436 | 9.171e-06 | [4.279e-02, 0.111] |
| beta[1] | 0.8788 | 2.603e-02 | 33.757 | 8.371e-250 | [ 0.828, 0.930] |
| coef | std err | t | P>|t| | 95.0% Conf. Int. | |
| eta | 10.9362 | 2.815 | 3.885 | 1.022e-04 | [ 5.419, 16.453] |
| lambda | -0.1196 | 4.054e-02 | -2.951 | 3.172e-03 | [ -0.199,-4.016e-02] |
Verificamos que ao longo do período da amostra o ponto de "salto" da volatilidade ocorre em 2020, início do período da pandemia de covid. Pequenos "saltos" são verificados em parcelas de períodos diferentes, ocasionados por diversos eventos e turbulências no mercado acionário. Em relação ao último períodos da amostra, referente ao ano de 2023, verifica-se uma queda no valor da volatilidade.
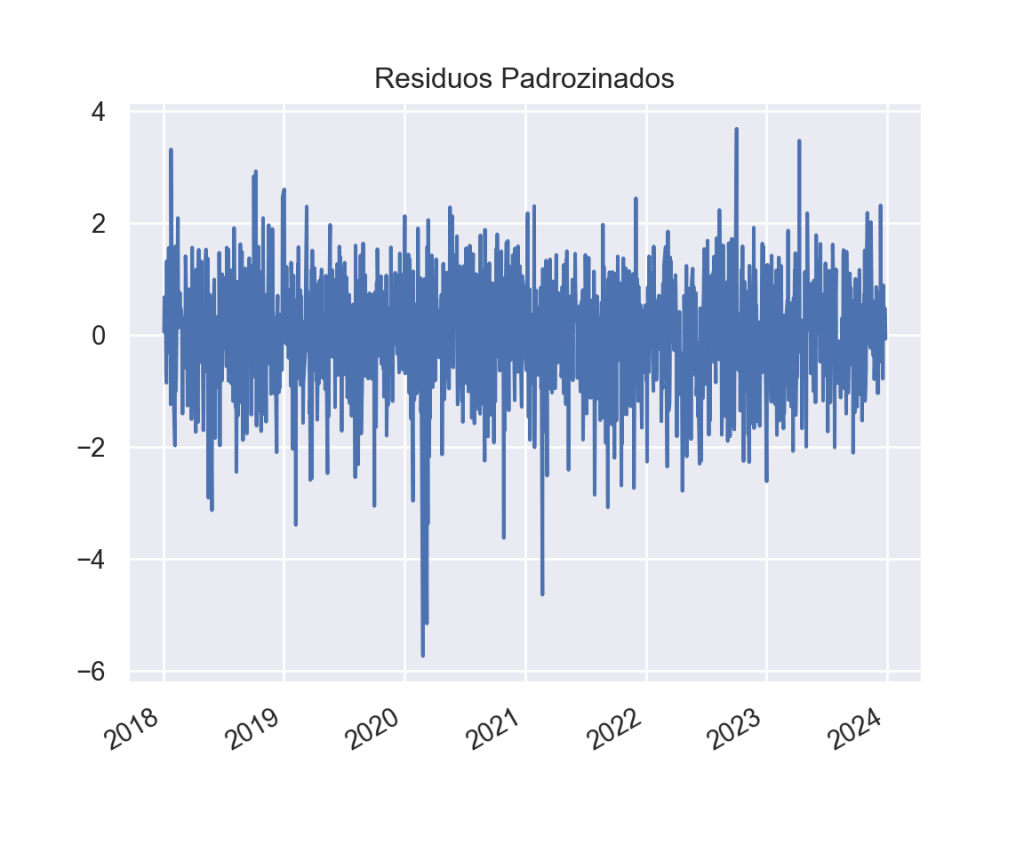
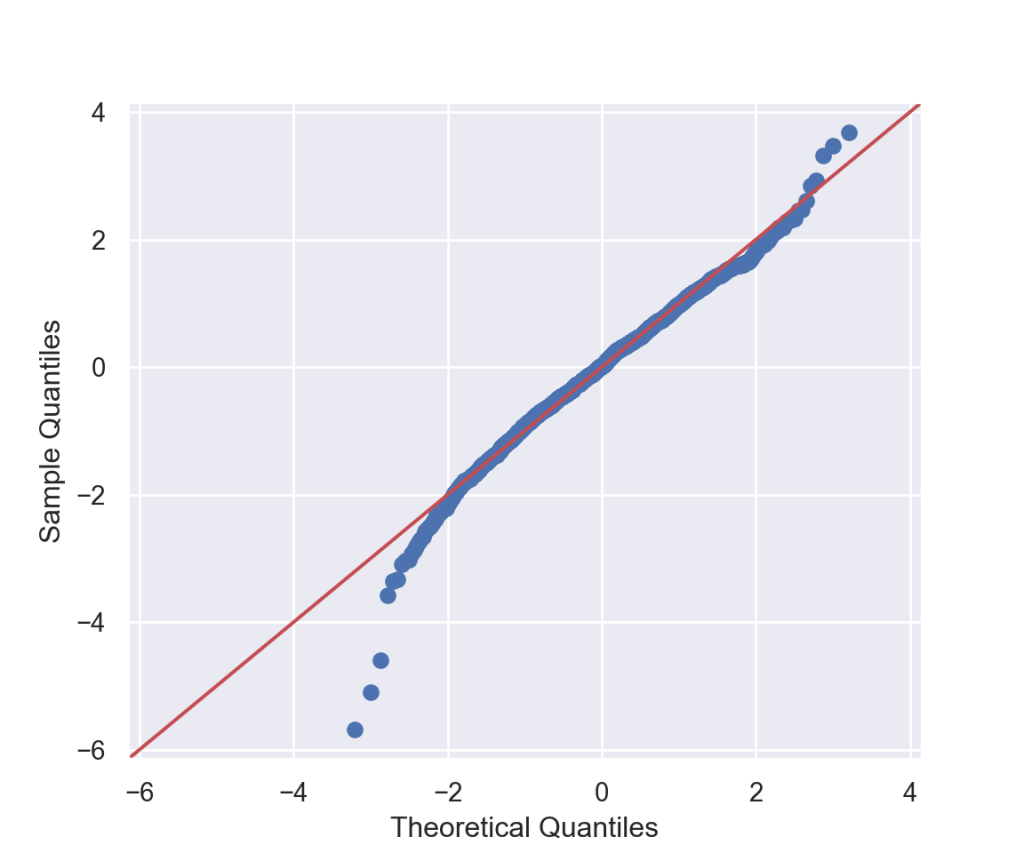
Resíduos Padronizados
Verificamos os valores dos resíduos padronizados para avaliar a qualidade do modelo. Abaixo, como pode-se evidenciar, temos um relativo bom desempenho dos resíduos, apresentando-se estacionário e com pequenas quantidades de outliers.
Volatilidade de Longo Prazo
A variância incondicional representa a estimativa da variância que a série temporal de retornos eventualmente convergirá, assumindo que a série é infinitamente longa e que as condições de mercado permanecem constantes no longo prazo. É dada por:
Podemos comparar a variância incondicional estimada em janelas móveis com a variância amostral também em janelas móveis. Assim, podemos ter os seguintes critérios de análise:
- Se a Volatilidade Amostral é Maior que a Volatilidade Incondicional:
- Isso pode indicar que, no curto prazo, a série de retornos está experimentando picos de volatilidade acima do nível que se esperaria no longo prazo de acordo com o modelo GARCH. Pode sugerir períodos de maior instabilidade ou eventos anômalos na série temporal.
- Se a Volatilidade Amostral é Menor que a Volatilidade Incondicional:
- Isso pode sugerir que, no curto prazo, a série de retornos está experimentando uma volatilidade abaixo da média esperada no longo prazo pelo modelo GARCH. Pode indicar um período de estabilidade relativa ou menor variação nos retornos.
T. Bollerslev, “Generalized Autoregressive Conditional Heteroscedasticity”, Journal of Econometrics, 31 (1986): 307–27.
R. Engle “Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of UK Inflation”, Econometrica, 50 (1982): 987–1008.
Quer aprender mais?
Clique aqui para fazer seu cadastro no Boletim AM e baixar o código que produziu este exercício, além de receber novos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas diretamente em seu e-mail.

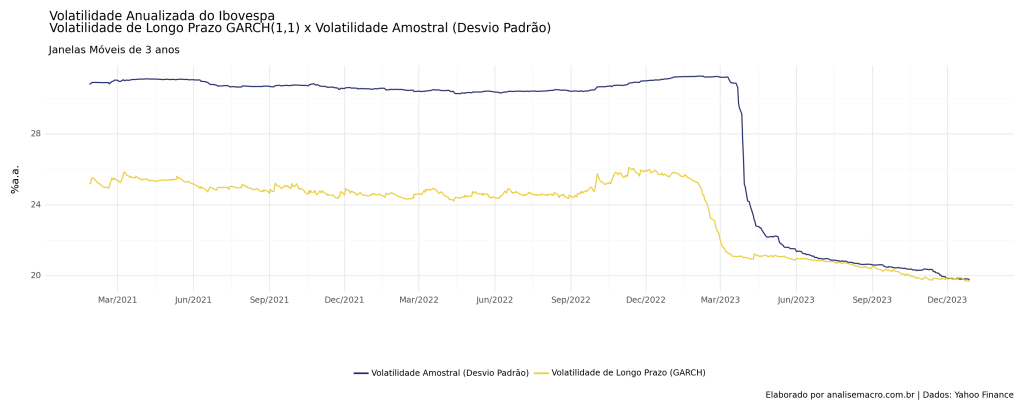
![Rendered by QuickLaTeX.com \[\sigma_t^2 = \omega + \sum_{i=1}^p \alpha_i a^2_{t-i} + \sum_{i=1}^q \beta_i \sigma^2_{t-i}\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-f73b7efa6aee8254b14d93f347890ad9_l3.png)