Neste artigo, conduzimos uma análise exploratória dos Betas estimados das ações no mercado acionário brasileiro utilizando a linguagem de programação Python. Optamos por segmentar cada empresa de acordo com seu setor, com o objetivo de examinar as distribuições de seus riscos de mercado. Adicionalmente, elaboramos classificações de portfólio com base na alocação de betas elevados e baixos, a fim de avaliar a eficácia da estratégia proposta pelo Modelo de Precificação de Ativos de Capital (CAPM). Isso nos permitiu realizar um teste de excesso de retorno e traçar a Security Market Line como parte da avaliação da formulação proposta.
Beta
De acordo com o Modelo de Precificação de Ativos de Capital (CAPM) de Sharpe (1964), Lintner (1965) e Mossin (1966), a variação transversal nas taxas de retorno esperadas dos ativos deve ser uma função da covariância entre o excesso de retorno do ativo e o excesso de retorno do portfólio de mercado. O coeficiente de regressão dos excessos de retornos de mercado nos excessos de retornos de ações é geralmente chamado de beta de mercado. Não entramos em detalhes sobre os fundamentos do beta de mercado, mas simplesmente remetemos a qualquer tratamento do CAPM para mais informações. Em vez disso, fornecemos detalhes sobre todas as funções que usamos para calcular os resultados. Em particular, aproveitamos conceitos computacionais úteis: estimação com janela deslizante e classificação de portfólios.
Para estimar os coeficientes de regressão do CAPM
Dados
Para o conjunto de amostra utilizamos dados de retornos diários de empresas participantes do Índice Bovespa. A lista de empresas foi obtida a partir da composição do Índice Bovespa no dia 30/10, que também inclui a separação por setores econômicos. Para o retorno livre de risco utilizamos o CDI diário. Os dados compreendem o período de 2021 até 10/2023.
Alunos inscritos no curso de Mercado Financeiro e Gestão de Portfólio com o Python têm a oportunidade de adquirir conhecimento em todas as etapas a seguir, além de obter uma compreensão teórica abrangente das principais ferramentas utilizadas no Mercado Financeiro.
Estimação de Beta
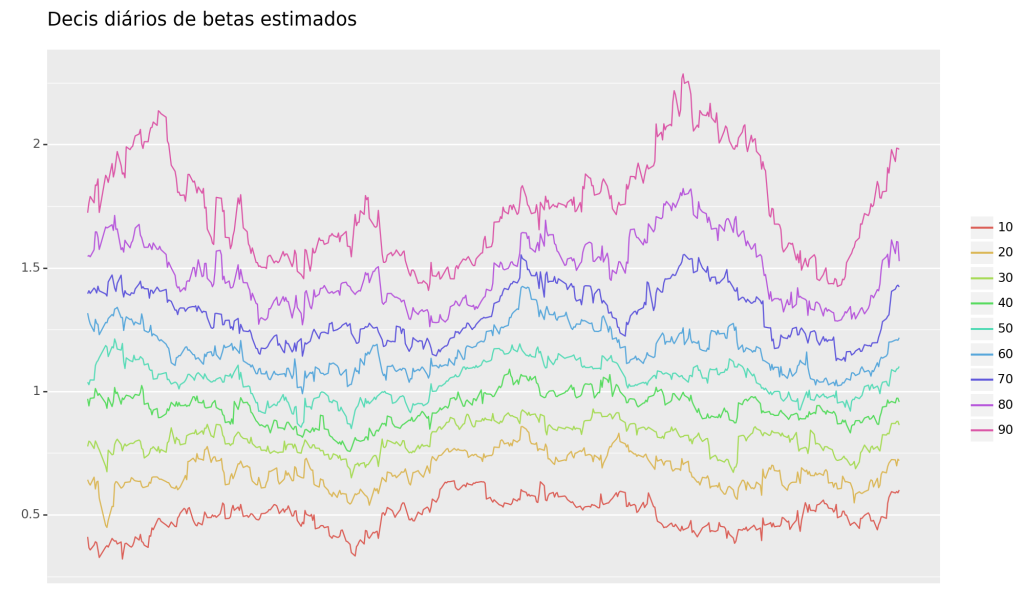
A estimativa do Beta diário móvel oferece a capacidade de avaliar a evolução e alteração da relação entre a ação/setores e o risco de mercado ao longo do tempo. Isso é alcançado ao excluir valores mais antigos que poderiam distorcer a contemporaneidade da relação de risco.
Além disso, ao examinar o Beta como uma Série Temporal para cada empresa, a oportunidade de agrupá-las por setores surge como uma abordagem valiosa. Isso possibilita a identificação de padrões e distribuições na relação de cada setor com o risco de mercado em um período específico, oferecendo insights mais abrangentes.
Código
| market | tickers | returns | beta | |
|---|---|---|---|---|
| Date | ||||
| 2022-02-16 | 0.004142 | ABEV3.SA | -0.012426 | 0.413070 |
| 2022-02-17 | -0.014753 | ABEV3.SA | 0.003655 | 0.346828 |
| 2022-02-18 | -0.007096 | ABEV3.SA | -0.002422 | 0.361883 |
| 2022-02-21 | -0.009651 | ABEV3.SA | -0.030766 | 0.402244 |
| 2022-02-22 | 0.010044 | ABEV3.SA | 0.061185 | 0.399989 |
| ... | ... | ... | ... | ... |
| 2023-11-03 | 0.026550 | YDUQ3.SA | 0.020394 | 1.152530 |
| 2023-11-06 | 0.002312 | YDUQ3.SA | 0.002744 | 1.164963 |
| 2023-11-07 | 0.006136 | YDUQ3.SA | 0.014016 | 1.172450 |
| 2023-11-08 | -0.001872 | YDUQ3.SA | -0.002148 | 1.169734 |
| 2023-11-09 | -0.001186 | YDUQ3.SA | -0.006268 | 1.176007 |
37238 rows × 4 columns
Distribuição de Beta por Setores do Índice Bovespa
Visualização: Boxplot
Visualização: Percentis
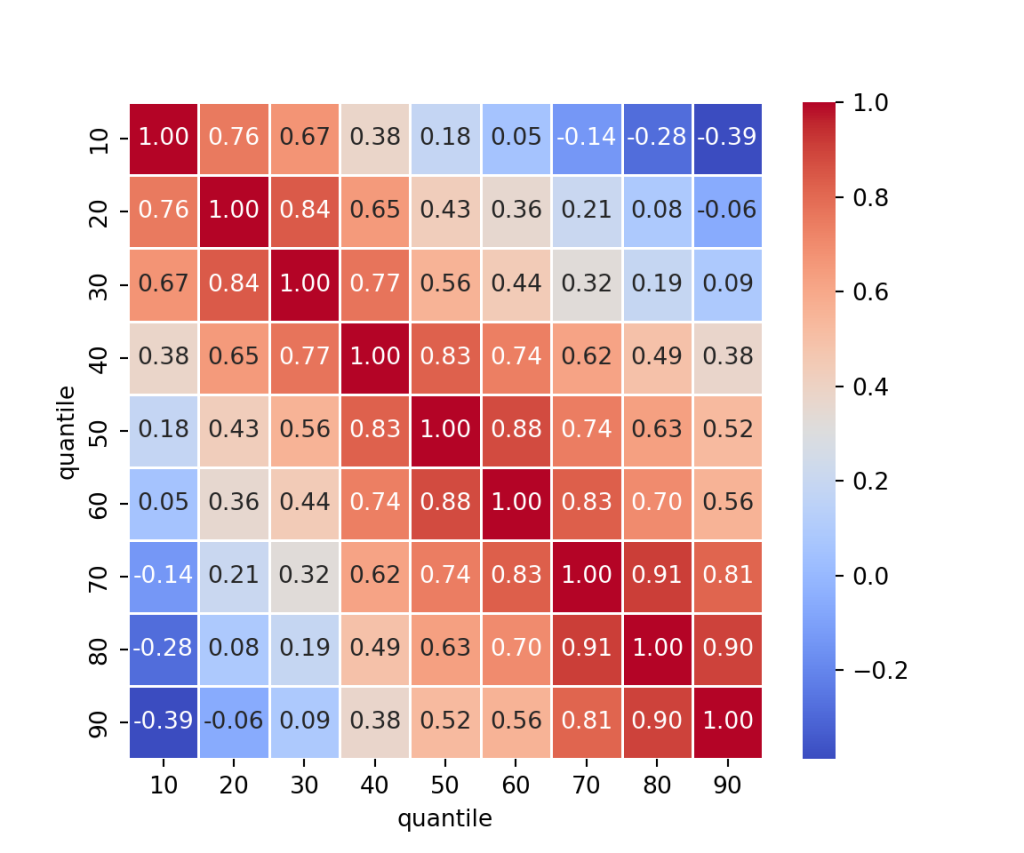
Visualização: Matriz de correlação dos percentis
Classificação de Portfólios
Exploramos as classificações de portfólio, uma das metodologias estatísticas mais amplamente empregadas na análise empírica de ativos. A aplicação central das classificações de portfólio é avaliar se uma ou mais variáveis podem antecipar retornos futuros em excesso.
Em linhas gerais, a abordagem consiste em agrupar ações individuais em portfólios, nos quais as ações dentro de cada conjunto compartilham semelhanças em relação a uma variável específica, como tamanho da empresa, valor, risco de mercado (beta), entre outras. Os diversos portfólios representam investimentos bem diversificados que variam conforme o nível da variável de classificação. Ao analisar a distribuição resultante, torna-se possível atribuir as discrepâncias (diferenças) na distribuição de retornos ao impacto da variável de classificação. Isso é particularmente útil na criação de fatores de risco, especialmente aqueles que têm frequências trimestrais e semestrais.
Introduzimos classificações de portfólio univariadas, neste caso, utilizando o Beta como a característica principal.
Um classificação de portfólio univariada considera apenas uma variável de classificação . Aqui,
denota a ação e
indica que a característica é observável pelos investidores no momento
. O objetivo é avaliar a relação transversal entre
e, tipicamente, os retornos em excesso da ação
no momento
como a variável dependente. Para ilustrar como as classificações de portfólio funcionam, utilizamos as estimativas para os betas de mercado como nossa variável de classificação. Um ponto importante, é que utilizamos os betas defasados de um período como variável de classificação para garantir que as classificações dependam apenas das informações disponíveis no momento em que criamos os portfólios.
Formulamos dois tipos diferentes de alocação para os portfólios: ponderados pelo percentual relativo na composição dos Ibovespa e outro igualmente ponderado.
Avaliação de performance dos portfólios
Podemos criar uma estratégia long-short com base nos dois portfólios: comprar o portfólio de alto beta e, ao mesmo tempo, fazer uma venda a descoberto no portfólio de baixa beta. Assim, a posição geral no mercado é zero líquido, ou seja, não é necessário investir dinheiro para realizar essa estratégia na ausência de atritos.
Calculamos o retorno médio e o erro padrão correspondente para testar se o portfólio long-short, em média, produz retornos em excesso positivos ou negativos. Na literatura de precificação de ativos, normalmente se ajusta para a autocorrelação usando as estatísticas de Newey e West (1987) para testar a hipótese nula de que os retornos médios em excesso do portfólio são iguais a zero.
Ponderado pela composição no Ibovespa
Código
| portfolio | Date | low | high | long_short |
|---|---|---|---|---|
| 0 | 2022-02-17 | -0.002092 | 0.003563 | 0.005654 |
| 1 | 2022-02-18 | -0.006824 | -0.021813 | -0.014989 |
| 2 | 2022-02-19 | -0.004749 | -0.015014 | -0.010264 |
| 3 | 2022-02-22 | -0.012890 | -0.026414 | -0.013525 |
| 4 | 2022-02-23 | 0.016211 | 0.017874 | 0.001663 |
| ... | ... | ... | ... | ... |
| 428 | 2023-11-04 | 0.022125 | 0.062428 | 0.040304 |
| 429 | 2023-11-07 | 0.008046 | -0.024795 | -0.032841 |
| 430 | 2023-11-08 | 0.004865 | 0.052297 | 0.047431 |
| 431 | 2023-11-09 | -0.003637 | -0.003785 | -0.000149 |
| 432 | 2023-11-10 | -0.012308 | -0.007796 | 0.004511 |
433 rows × 4 columns
Código
OLS Model:
long_short ~ 1
Coefficients:
Estimate Std. Error Statistic p-Value
Intercept -0.001 0.001 -1.613 0.107
Summary statistics:
- Number of observations: 433
- R-squared: -0.000, Adjusted R-squared: -0.000
- F-statistic: nan on 0 and 432 DF, p-value: nanIgualmente Ponderado
Código
| portfolio | Date | low | high | long_short |
|---|---|---|---|---|
| 0 | 2022-02-17 | 0.000735 | 0.006085 | 0.005350 |
| 1 | 2022-02-18 | -0.005420 | -0.016566 | -0.011146 |
| 2 | 2022-02-19 | -0.007282 | -0.010880 | -0.003598 |
| 3 | 2022-02-22 | -0.011638 | -0.027543 | -0.015906 |
| 4 | 2022-02-23 | 0.013678 | 0.018311 | 0.004634 |
| ... | ... | ... | ... | ... |
| 428 | 2023-11-04 | 0.022549 | 0.060494 | 0.037945 |
| 429 | 2023-11-07 | 0.008885 | -0.020103 | -0.028988 |
| 430 | 2023-11-08 | 0.005967 | 0.041303 | 0.035336 |
| 431 | 2023-11-09 | 0.000676 | -0.005234 | -0.005911 |
| 432 | 2023-11-10 | -0.006262 | -0.007398 | -0.001136 |
433 rows × 4 columns
Código
OLS Model:
long_short ~ 1
Coefficients:
Estimate Std. Error Statistic p-Value
Intercept -0.0 0.001 -0.681 0.496
Summary statistics:
- Number of observations: 433
- R-squared: -0.000, Adjusted R-squared: -0.000
- F-statistic: nan on 0 and 432 DF, p-value: nanOs resultados indicam que não podemos rejeitar a hipótese nula de que os retornos médios são iguais a zero. Portanto, nossa estratégia de portfólio usando a mediana como ponto de corte não gera retornos anormais. Isso é surpreendente ao reconsiderar o CAPM? Certamente é. O CAPM sugere que as ações de alto beta devem proporcionar retornos esperados mais elevados. Nossa classificação de portfólio imita implicitamente uma estratégia de investimento que financia ações de alto beta ao realizar vendas a descoberto de ações de baixo beta. Portanto, seria de se esperar que os retornos médios em excesso resultassem em um retorno acima da taxa livre de risco.
Classificação de diversos portfólios
Vamos avançar na classificação de portfólio. Queremos ser capazes de classificar ações em um número arbitrário de portfólios. Para este caso, a programação funcional é muito útil: definimos uma função que nos dá flexibilidade em relação à variável a ser usada para a classificação. Definimos o ponto de quebra que desejamos para criar o número de portfólio desejados. Em seguida, atribuímos portfólios às ações.
Em algumas aplicações, a variável usada para a classificação pode estar agrupada (por exemplo, em um limite inferior de 0). Nesse caso, múltiplos pontos de quebra podem ser idênticos, levando a portfólios vazios. Da mesma forma, alguns portfólios podem ter um número muito pequeno de ações no início da amostra. Casos nos quais o número de constituintes do portfólio difere substancialmente devido à distribuição das características exigem consideração cuidadosa e, dependendo da aplicação, podem exigir abordagens de classificação personalizadas.
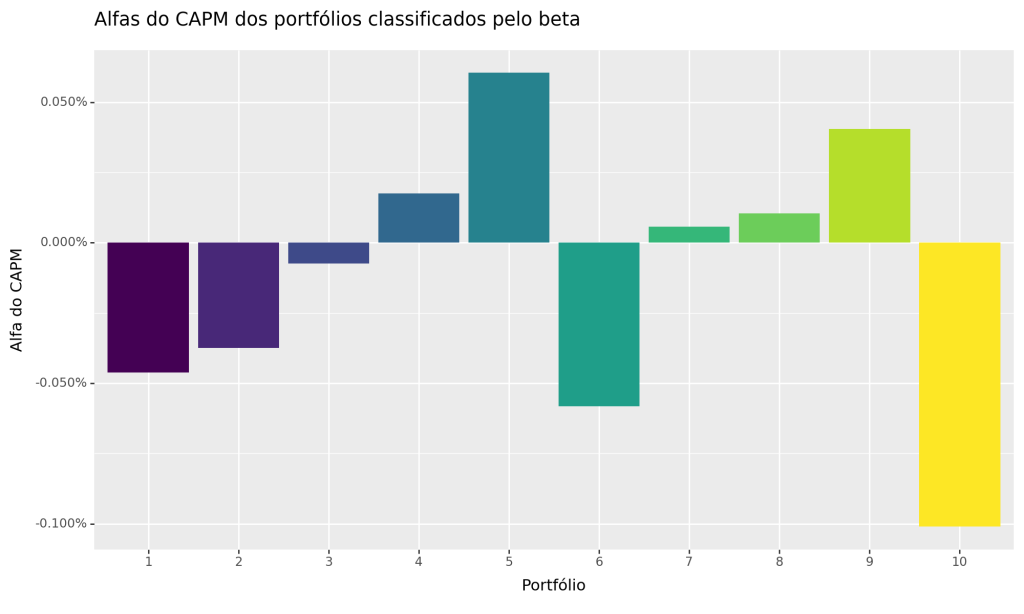
Visualização: Alpha dos Portfólios Classificados
No próximo passo, calculamos estatísticas resumidas para cada portfólio de beta. Em particular, calculamos alfas ajustados pelo CAPM, o beta de cada portfólio e os retornos médios.
Como consequência, conseguimos ilustrar os Alphas de cada Portfólio construído. Veja que para o caso do Mercado Acionário Brasileiro, temos uma relação não bem definida entre beta e retornos futuros de ações, o que contradiz as previsões do CAPM. De acordo com o CAPM, os retornos deveriam aumentar com o beta entre os portfólios, e os retornos ajustados ao risco deveriam ser estatisticamente indistinguíveis de zero.
Código
| portfolio | alpha | beta | ret | |
|---|---|---|---|---|
| 0 | 1 | -0.000462 | 0.370372 | -0.000583 |
| 1 | 2 | -0.000374 | 0.625378 | -0.000578 |
| 2 | 3 | -0.000074 | 0.771182 | -0.000325 |
| 3 | 4 | 0.000175 | 0.884648 | -0.000113 |
| 4 | 5 | 0.000604 | 1.000301 | 0.000278 |
| 5 | 6 | -0.000582 | 1.106388 | -0.000942 |
| 6 | 7 | 0.000057 | 1.255543 | -0.000352 |
| 7 | 8 | 0.000105 | 1.433910 | -0.000362 |
| 8 | 9 | 0.000405 | 1.577735 | -0.000109 |
| 9 | 10 | -0.001011 | 2.020611 | -0.001669 |
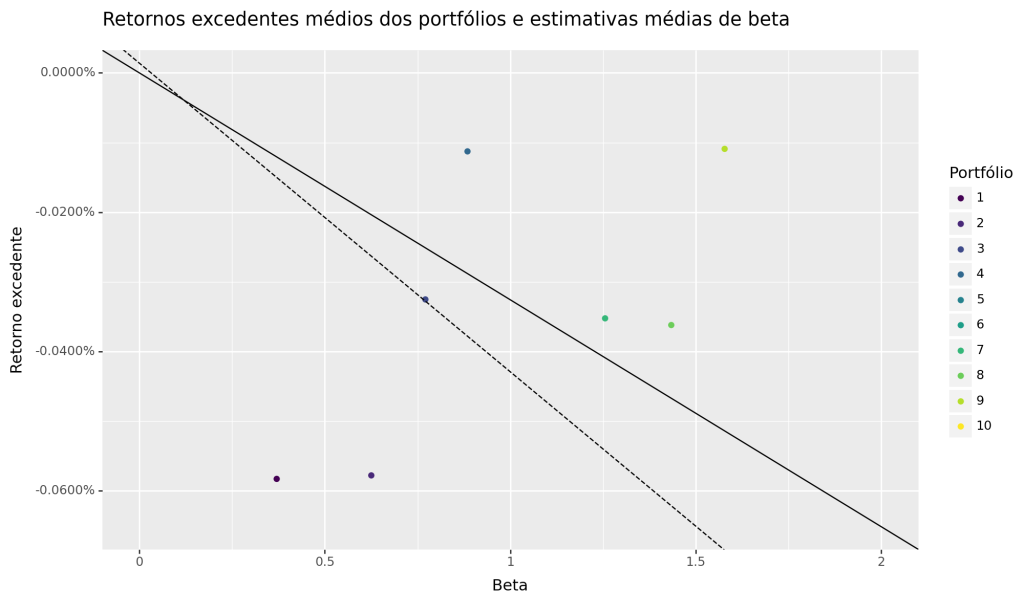
Visualização: Security Market Line dos Portfólios Classificados
O CAPM prevê que nossos portfólios deveriam estar na linha do mercado de títulos (SML). A inclinação da SML é igual ao prêmio de risco de mercado e reflete o trade-off entre risco e retorno em qualquer momento específico. O gráfico abaixo ilustra a linha do mercado de títulos: Observamos que a SML é negativa, bem como há alta dispersão dos Retornos em relação ao Beta indicando que não há nenhuma relação bem definida dos Betas para o mercado acionário estudado.
Quer aprender mais?
Clique aqui para fazer seu cadastro no Boletim AM e baixar o código que produziu este exercício, além de receber novos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas diretamente em seu e-mail.
Referências
Christoph Frey, Chistoph Scheuch, Stefan Voigt, Patrick Weiss. Tidy Finance with Python. https://www.tidy-finance.org/python/