Aplicação de Cadeias de Markov no mercado financeiro com o R

A ideia da Cadeia de Markov é construir um sistema matemático que visa calcular probabilidades de transição de um estado para o outro de acordo com um conjunto de regras probabilísticas. São chamados processos "sem memória", pois dependem somente da informação do presente. No post de hoje, vamos realizar uma introdução a essa classe de modelos realizando uma simples aplicação para o mercado financeiro.

Cadeias de Markov

Cadeias de Markov fazem parte da disciplina de processos estocásticos e são usadas em diversas tipos de áreas. Uma cadeia de Markov é um processo estocástico que satisfaz a propriedade de markov, o que significa que o passado e o futuro são independentes quando o presente é conhecido. Isso significa que se tivermos o conhecimento o estado atual do processo, então nenhuma informação adicional de seus estados passados são necessários para criar a melhor previsão do futuro.

A ideia principal é que uma variável pode ser definida em estados. Exemplo: o clima pode possuir três estados, ensolarado, chuvoso ou nublado, portanto, possui estados discretos. Além dos estados, deve conter um espaço, usualmente o tempo, este em que pode ser discreto ou contínuo. No exercício a seguir trabalharemos com cadeia de Markov em tempo discreto.

Formalmente,  de acordo com Ross (2012), tenha-se uma sequência de variáveis aleatórias dentro do conjunto de valores possíveis em . Interpreta-se como o estado de algum sistema no tempo , e portanto, diz-se que o sistema está no estado no tempo se . Essa sequência de variáveis aleatória formam uma cadeia de Markov se cada vez que o sistema estiver no estado , existir uma probabilidade fixa de que o sistema siga no estado definida com . Para

(1)  

A partir do conhecimento das probabilidades de transição e do conhecimento do estado inicial, é possível, em tese, calcular todas as probabilidades de interesse. É possível facilitar a construção desse cálculo, para n estados, por meio de um vetor de probabilidade inicial e de uma matriz de probabilidade . O sistema é representado pelo seguinte cálculo.

E com   representando o numero de passos do sistema, é possível conhecer as probabilidades de passos a frente por meio do conhecimento das probabilidades presentes.

Aplicação

Uma cadeia de Markov pode ser útil para prever as condições do futuro do mercado. Para tanto, é necessário dizer que o preço de uma ação segue as propriedades de Markov em tempo discreto, sendo representada por dois estados:

• Tendência positiva: quando o preço no tempo atual é maior do que o preço no tempo imediatamente anterior
• Tendência negativa: quando o preço no tempo atual é menor do que o preço no tempo imediatamente anterior

Vamos calcular a matriz de probabilidade dos estados do preço de uma ação em determinado período de tempo. Para tanto, vamos coletar os dados da ITUB4, durante o período de 2019 até o fim de 2021. O foco será calcular as probabilidades de ocorrências do estados positivo e negativo de acordo com a regra criada acima, em   passos a frente. Para tanto, criaremos um vetor de estados dos dados do preço passado de acordo, e em seguida, utilizaremos o pacote {markovchain} para estimar a matriz de transição por meio da máxima verossimilhança e por fim, por meio do calculo de matrizes, obtemos as probabilidades futuras dos estados.

library(quantmod)
library(xts)
library(timetk)
library(markovchain)
library(dplyr)
library(ggplot2)

</pre>
# Ativo
asset <- "ITUB4.SA"
# Início
inicio <- "2019-01-01"
# Fim
fim <- "2021-12-31"

# Importa os dados
getSymbols(asset,
from = inicio,
to = fim )

# Tratamento e criação dos estados
price_itub <- Cl(ITUB4.SA) |>
to.monthly(indexAt = "yearmon", OHLC = FALSE) |>
tk_tbl(preserve_index = TRUE,
rename_index = "date") |>
mutate(estados = if_else(ITUB4.SA.Close > dplyr::lag(ITUB4.SA.Close), "positivo", "negativo"))

# Pega o vetor de estados
estados <- price_itub$estados[-1]
<pre>

Com os estados definidos dentro de um vetor, utilizaremos o pacote {markovchain} para realizar a inferência da matriz de transição

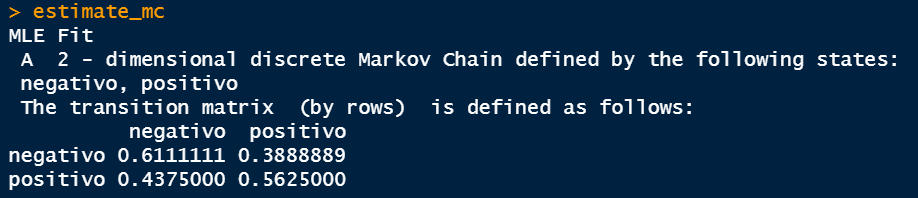
</pre>
# Estima a matriz de probabilidades de transição (MLE)
mc_fit <- markovchainFit(data = estados)

# Matriz estimada
estimate_mc <- mc_fit$estimate
<pre>

Acima, obtemos a matriz de transição de acordo com os estados do período. A leitura é feita por linhas, isto é, há 61% de chances de um estado negativo continuar no estado negativo caso haja uma transição, enquanto há 38% de chance de sair do estado negativo para o positivo. Por outro lado, caso esteja inicialmente em um estado positivo, há 44% de chance de continuar no mesmo estado, enquanto há 56% de chance de ir do estado positivo para o negativo.

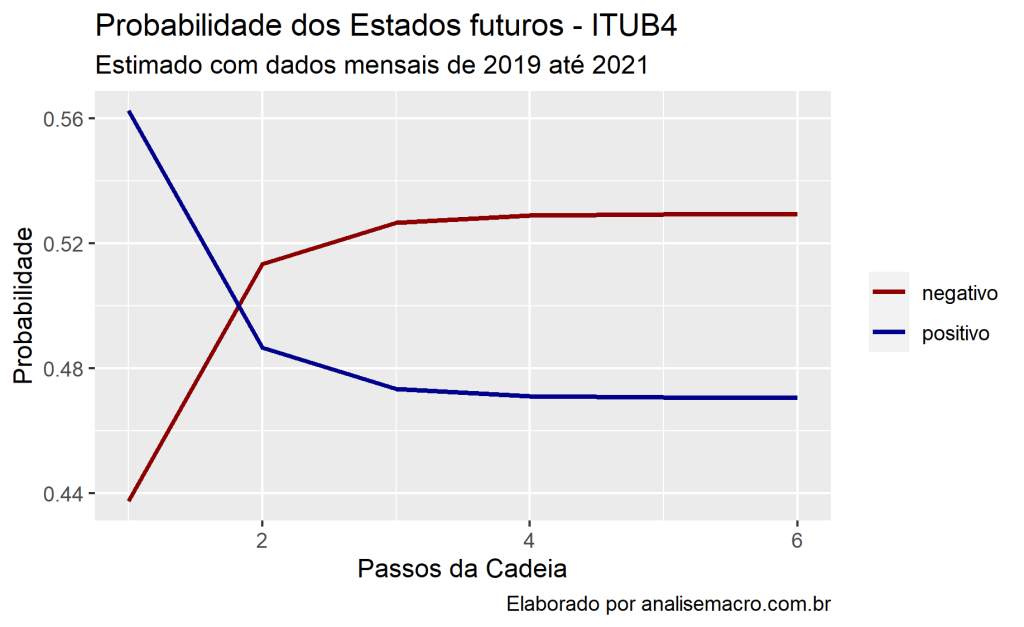
Abaixo, podemos obter as probabilidades em passos a frente. Tomaremos como estado inicial o último estado computado no vetor (positivo).

</pre>
# Estado inicial
init_state <- c("negativo" = 0,
"positivo" = 1)

# Inicializa
p_prob <- c()
n_prob <- c()

# Calcula as probabilidades em 6 passos
for(k in 1:6){
nsteps <- init_state * estimate_mc ^ k
n_prob[k] <- nsteps[1,1]
p_prob[k] <- nsteps[1,2]
}

# Transforma em data frame
p_prob_df <- as.data.frame(p_prob) |>
mutate(group = 'positivo',
iter = 1:6) |>
rename(value = p_prob)

n_prob_df <- as.data.frame(n_prob) |>
mutate(group = 'negativo',
iter = 1:6) |>
rename(value = n_prob)

steps <- rbind(p_prob_df, n_prob_df)
<pre>

# Plota as probabilidades em 6 passos
ggplot(steps, aes(x = iter, y = value, color = group))+
geom_line(size = 1)+
scale_color_manual(NULL, values = c("darkred", "darkblue"))+
labs(x = 'Passos da Cadeia',
y = 'Probabilidade',
title = "Probabilidade dos Estados futuros - ITUB4",
subtitle = "Estimado com dados mensais de 2019 até 2021",
caption = "Elaborado por analisemacro.com.br")

______________________________________

Quer saber mais?

Veja nossa trilha de Finanças Quantitativas.

______________________________________

Referências

Ross, S. Probabilidade: Um Curso Moderno com Aplicações. Bookman, 2012.