Aplicação
Para obter o código e o tutorial deste exercício faça parte do Clube AM e receba toda semana os códigos em R/Python, vídeos, tutoriais e suporte completo para dúvidas.
Como mencionado, o HMM é amplamente utilizado diversas aplicações de diferentes áreas, como exemplos temos: Inteligência Artificial, reconhecimento de fala, análise de sequências biológicas e, no contexto financeiro, identificação de mudanças de regime em séries temporais, como a detecção de períodos de alta e baixa volatilidade em mercados.
? Objetivo
Neste exercício nosso objetivo é o e detectar mudanças de regime nos retornos mensais do Ibovespa, identificando períodos de alta volatilidade (mercado de crise) e baixa volatilidade (mercado estável).
? Passos
- Coletar os dados mensais do Ibovespa
- Calcular os retornos logarítmicos (%)
- Ajustar um Modelo Oculto de Markov (HMM) para detectar regimes
- Analisar os estados e probabilidades de volatilidade previstos
1️⃣ Baixando os Dados do Ibovespa
Vamos coletar os dados do Yahoo Finance usando a biblioteca yfinance.
Código
| Price | Date | Close | High | Low | Open | Volume | Retorno |
|---|---|---|---|---|---|---|---|
| Ticker | ^BVSP | ^BVSP | ^BVSP | ^BVSP | ^BVSP | ||
| 0 | 2000-02-01 | 17660.0 | 18886.0 | 16389.0 | 16389.0 | 0 | 7.475284 |
| 1 | 2000-03-01 | 17820.0 | 19047.0 | 16922.0 | 17668.0 | 0 | 0.901923 |
| 2 | 2000-04-01 | 15538.0 | 17826.0 | 14029.0 | 17826.0 | 0 | -13.703279 |
| 3 | 2000-05-01 | 14957.0 | 15944.0 | 13556.0 | 15596.0 | 0 | -3.810922 |
| 4 | 2000-06-01 | 16728.0 | 17396.0 | 14967.0 | 14967.0 | 0 | 11.190454 |
2️⃣ Visualizar a Série dos Retornos Mensais
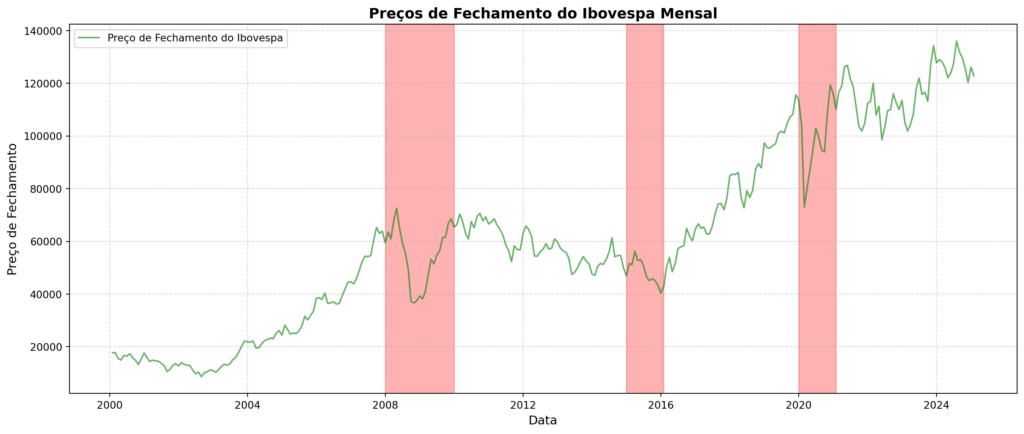
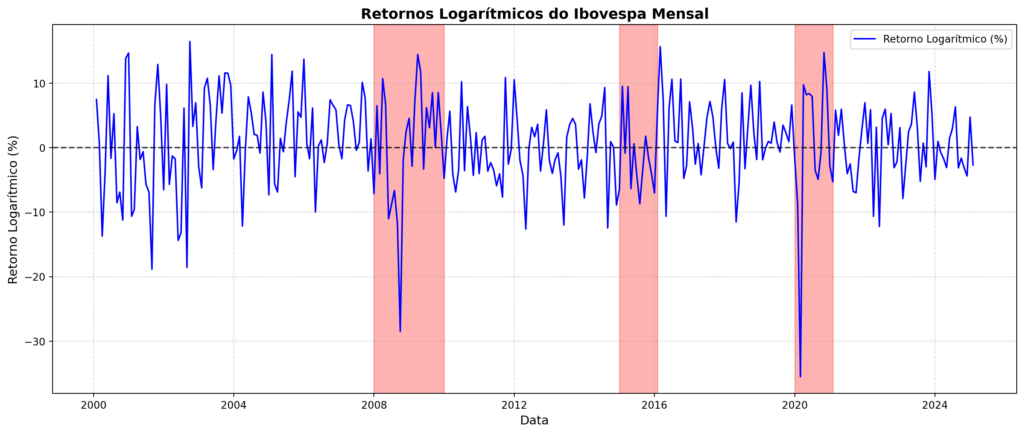
Nesta etapa visualizamos os pontos do Ibovespa e os retornos logarítmicos.
3️⃣ Aplicando o Modelo Oculto de Markov (HMM)
Agora, ajustamos um HMM. Por suposto, temos entre 2 e 3 estados a serem considerados:
- Baixa Volatilidade
- Alta Volatilidade
- Neutro (mercado sem direção)
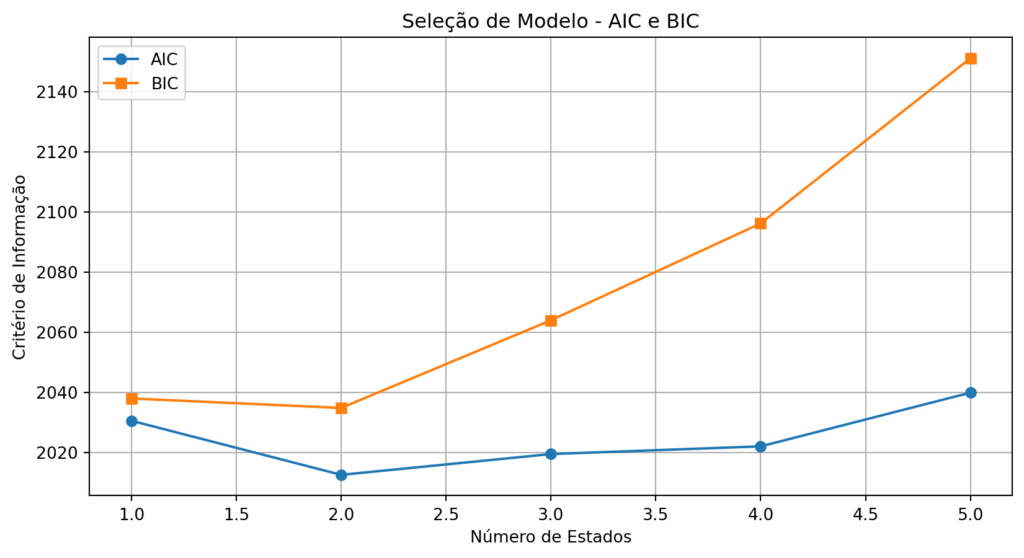
Uma forma interessante de obter o número de estados é através da seleção via critério de informação. Para isso computamos o AIC e BIC para diferentes estados (1 a 5 no caso abaixo) através de uma iteração. Os resultados demonstram os valores de cada critério para cada número de estado, e assim, podemos escolher que possui o menor valor.
Pelos critérios, vemos que a escolha feita foi de 2 estados. Prosseguimos para a construção do modelo.
4️⃣ Analisando os Regimes de Volatilidade
Agora, vamos visualizar os regimes previstos pelo modelo.
O gráfico exibe os regimes de volatilidade do Ibovespa identificados pelo HMM. Os pontos azuis representam períodos de baixa volatilidade, enquanto os pontos vermelhos indicam momentos de alta volatilidade, geralmente associados a choques econômicos ou crises de mercado. A linha tracejada preta em zero auxilia na interpretação dos retornos positivos e negativos ao longo do tempo.
Observa-se que os períodos de alta volatilidade são esporádicos e concentrados em momentos de crise, como a crise de 2008 e a pandemia de 2020. Já os períodos de baixa volatilidade dominam a série, indicando que o Ibovespa tende a permanecer mais tempo em um regime de estabilidade.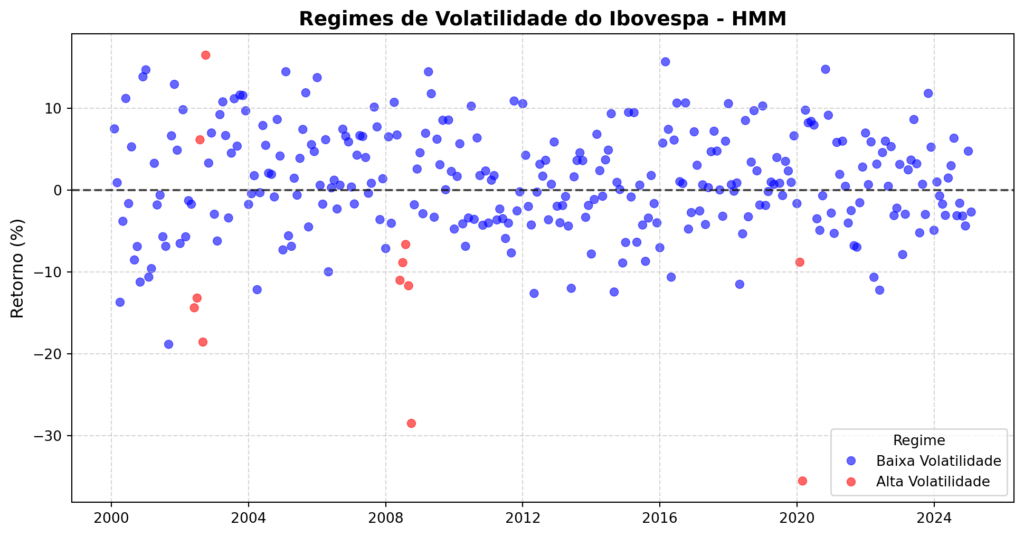
5️⃣ Analisando Probabilidades de Regime
Probabilidade dos regimes
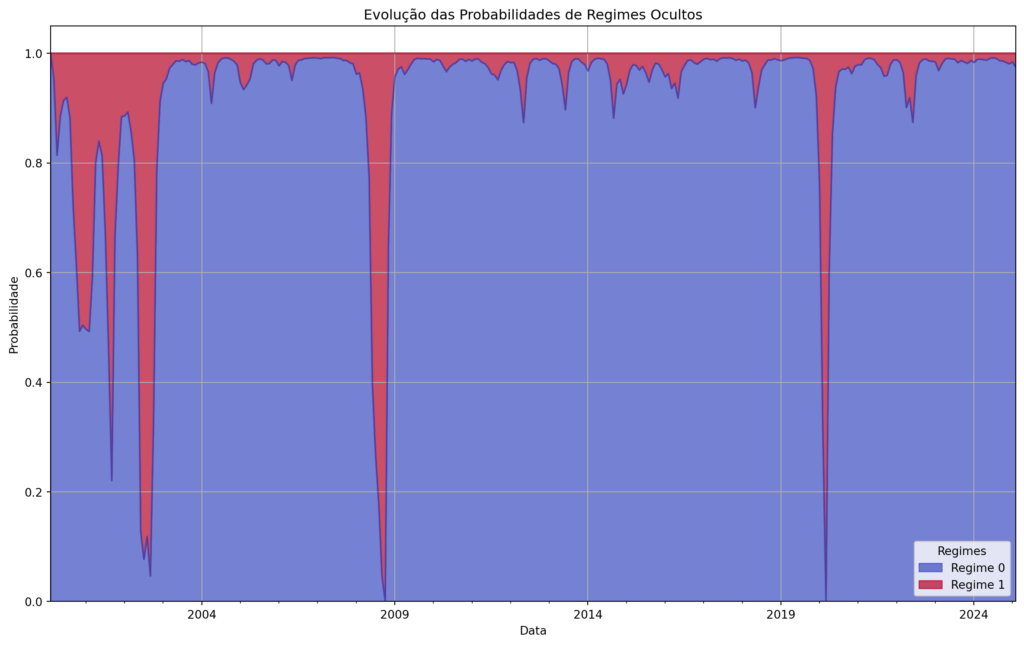
O gráfico exibe a evolução das probabilidades dos regimes ocultos do Ibovespa ao longo do tempo, conforme estimado pelo modelo HMM. A cor azul representa o Regime 0 (baixa volatilidade), enquanto a cor vermelha representa o Regime 1 (alta volatilidade). Percebe-se que o mercado passa a maior parte do tempo no Regime 0, mas transita para o Regime 1 em momentos de crise ou choques econômicos.
Os períodos de alta volatilidade são pontuais, aparecendo principalmente em crises como a de 2008 e a pandemia de 2020. O modelo indica transições bruscas entre os regimes, mostrando que choques no mercado levam a mudanças abruptas na dinâmica dos retornos.
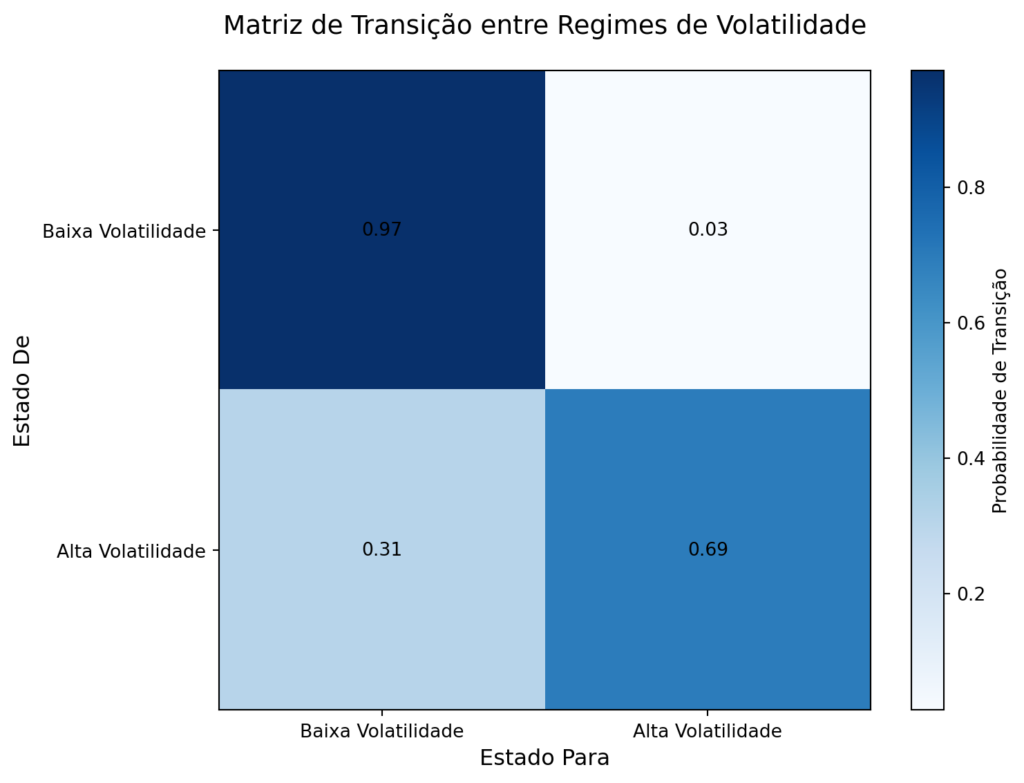
Matriz de Transição
A matriz de transição ilustra as probabilidades de mudança entre os estados de volatilidade identificados pelo modelo HMM: Regime 0 (baixa volatilidade) e Regime 1 (alta volatilidade). No gráfico, os eixos “Estado De” e “Estado Para” representam, respectivamente, o estado atual e o estado futuro, enquanto as cores indicam a probabilidade de transição entre eles.
Observa-se que o modelo tende a permanecer no Regime 0 por longos períodos, refletindo a estabilidade predominante do mercado. Transições para o Regime 1 são menos frequentes e ocorrem principalmente durante crises, indicando mudanças abruptas na dinâmica dos retornos.
Tempo Esperado em cada regime
O tempo esperado em cada regime indica quanto tempo, em média, o modelo permanece em um determinado estado antes de transitar para outro. Essa métrica é calculada a partir da matriz de transição do modelo HMM e fornece informações sobre a duração dos regimes de volatilidade.
Tempo Esperado em Cada Regime:
Regime 0: 35.95 meses
Regime 1: 3.28 meses- Regime 0 (Baixa Volatilidade): O modelo permanece, em média, 35.95 meses nesse regime. Isso reflete a tendência do mercado de ficar estável por longos períodos, com retornos menos voláteis.
- Regime 1 (Alta Volatilidade): O tempo esperado é de apenas 3.28 meses, indicando que períodos de alta volatilidade são curtos e pontuais, geralmente associados a crises ou choques econômicos.
Volatilidade por Regime
A volatilidade dos regimes foi calculada a partir do desvio padrão dos retornos mensais do Ibovespa, agrupados por cada regime identificado pelo modelo HMM. Essa métrica mede a dispersão dos retornos em cada estado, indicando o nível de incerteza ou risco associado a cada regime.
Volatilidade dos Regimes:
Regime
0 6.171395
1 13.680815
Name: Retorno, dtype: float64- Regime 0 (Baixa Volatilidade): A volatilidade é de 6.17%, refletindo um mercado estável, com retornos menos dispersos e menor risco.
- Regime 1 (Alta Volatilidade): A volatilidade sobe para 13.68%, indicando um mercado mais instável, com retornos altamente dispersos e maior incerteza, típico de períodos de crise ou choques econômicos.
Quer aprender mais?
Conheça nossa Formação do Zero à Análise de Dados Econômicos e Financeiros usando Python e Inteligência Artificial. Aprenda do ZERO a coletar, tratar, construir modelos e apresentar dados econômicos e financeiros com o uso de Python e IA.