O que é o Beta de Mercado?
O Beta de Mercado é uma medida financeira que representa a sensibilidade ou volatilidade de um ativo em relação ao mercado como um todo. Em outras palavras, o Beta de Mercado mede a resposta esperada de um ativo a movimentos no mercado de referência, geralmente representado por um índice amplo, como o índice geral de ações de um país (por exemplo, o S&P 500 nos EUA e o Ibovespa no Brasil).
O Beta é importante porque ele mede o risco de um investimento que não pode ser reduzido por meio da diversificação. Em outras palavras, ele não mede o risco de um ativo de investimento quando considerado isoladamente, mas a quantidade de risco que o investimento adiciona ao portfólio.
A importância do Beta de Mercado para a gestão de portfólio está relacionada ao processo de diversificação e controle de risco. Ao selecionar ativos para compor um portfólio, os investidores buscam otimizar o retorno esperado em relação ao risco assumido.
O Beta de Mercado é um dos fatores que ajuda os gestores de portfólio a entender como um ativo específico se comporta em relação ao mercado. Com essa informação, é possível construir uma carteira diversificada que busca minimizar o risco sistêmico, ou seja, o risco relacionado a todo o mercado.
Como o mercado possui um Beta de 1, uma ação com Beta maior que 1 indica que a ação é teoricamente mais arriscada. Por exemplo, uma ação com Beta de 1,2 implica que a ação é cerca de 20% mais volátil do que o mercado geral. Da mesma forma, uma ação com Beta menor que 1 implica que é menos volátil.
CAPM
O Beta de uma ação é necessário para calcular o prêmio de risco para uma ação individual.
Quanto maior o Beta, mais arriscada é a ação e, portanto, maior é a taxa de retorno requerida. O CAPM, que significa "Modelo de Precificação de Ativos Financeiros", é um modelo clássico na gestão de portfólio.
A equação do CAPM demonstra como determinar a taxa de retorno requerida de um ativo de investimento. Usando ações como exemplo: para calcular a taxa de retorno requerida, precisamos da taxa livre de risco, do retorno esperado do mercado e do Beta da ação como entradas para a equação.
Onde:
é o retorno esperado do ativo;
é a taxa livre de risco (retorno de um ativo considerado livre de risco, como títulos do governo);
é o Beta do ativo em relação ao mercado;
é o retorno esperado do mercado;
é o prêmio de mercado.
Comumente, a taxa livre de risco é representada pelo retorno dos títulos do governo, o retorno esperado do mercado é representado pelo Ibovespa, e o Beta é multiplicado pela diferença entre o retorno do mercado e a taxa livre de risco, ou prêmio de mercado, para determinar o retorno adicional esperado de uma ação.
O CAPM é muito utilizado na prática para calcular o custo de capital de um ativo ou para determinar se um ativo está subvalorizado ou sobrevalorizado em relação ao seu risco. Além disso, é uma ferramenta importante para a tomada de decisões de investimento em uma abordagem de gestão ativa de portfólio, permitindo aos gestores avaliar o retorno esperado em relação ao risco de cada ativo e, assim, escolher uma combinação ótima de ativos que maximize o retorno ajustado ao risco.
Como calcular o Beta?
O Beta é um coeficiente da equação e que deve ser estimada, baseando-se nas entradas de dados de retornos do ativo e do ativo referência (retornos de mercado). O cálculo de beta segue:
Ou seja, a Covariância do Retorno do Ativo com o Retorno do Mercado dividido pela Variância do Retorno do Mercado.
Como calcular o Beta dinâmico?
O Beta calculado acima resulta no coeficiente da amostra, entretanto, é interessante obter estimativas do indicador para cada período de tempo, levando em consideração as informações do período em questão. Portanto, podemos obter esse Beta dinâmico por meio da Variância estimada por modelos do tipo ARCH (e consequentemente pela Covariância).
Sendo assim, obtemos o Beta Dinâmico por meio da equação:
Em que
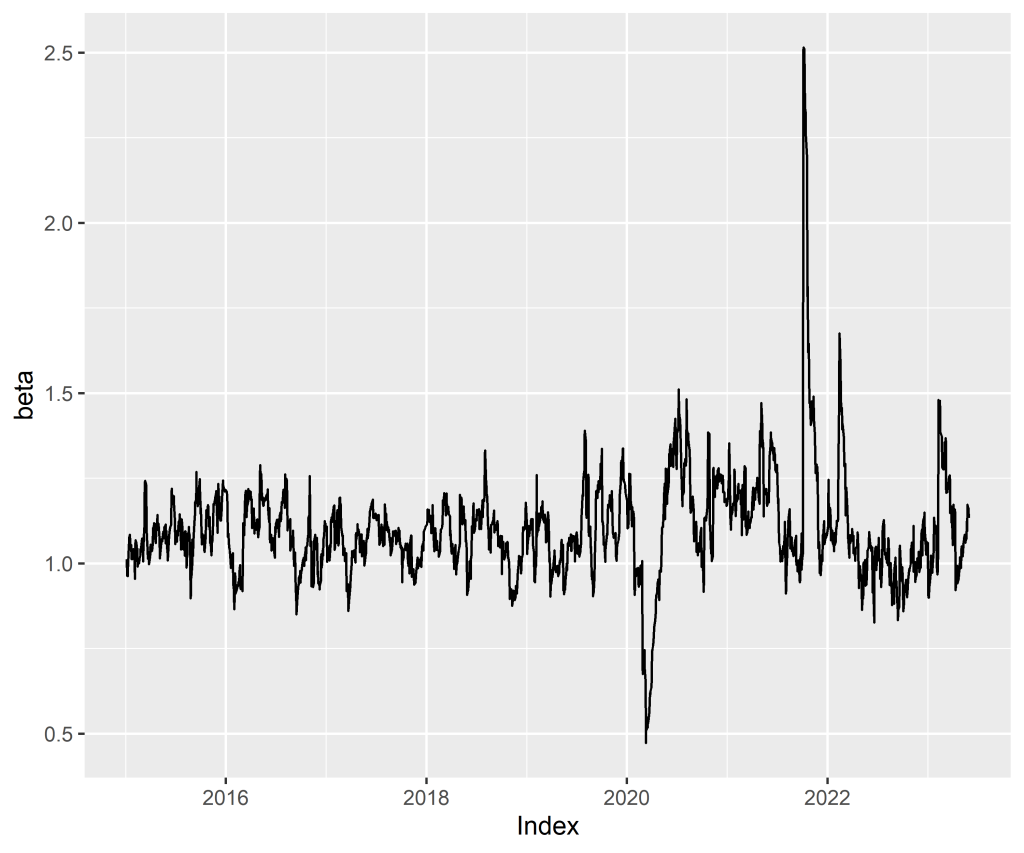
Exemplo: Beta Dinâmico entre ITUB4 e Ibovespa
Para obter todo o código em R e Python para os exemplos abaixo, faça parte do Clube AM, o repositório de códigos da Análise Macro, contendo exercícios semanais.
O exemplo abaixo demonstra o Beta Dinâmico entre ITUB4 e Ibovespa, calculado a partir de um GARCH (1,1) com distribuição t de student assimétrica. Os dados referem-se ao período de 2015 a junho de 2023 em periodicidade diária com retorno simples. A estimativa foi feita tanto utilizando o R quanto o Python.
_____________________
Quer saber mais?
Veja nossa trilha de cursos de Finanças Quantitativas