Uma aplicação interessante da variância calculada a partir dos modelos da família ARCH é a possibilidade de obter os pesos para um portfólio de mínima variância ao longo do tempo. Veremos neste artigo como obter as medidas para um portfólio de dois ativos e a possibilidade do cálculo por meio do R e do Python.
Minimização de Portfólio
Minimização de portfólio é um conceito muito importante para a área de gestão de carteiras. Refere-se ao processo de selecionar ativos de forma a criar uma carteira de investimentos que tenha o menor nível possível de risco para um determinado nível de retorno esperado.
A ideia por trás da minimização de portfólio é encontrar a combinação ideal de ativos que reduza a volatilidade e o risco geral da carteira, enquanto ainda busca alcançar um retorno desejado. Isso é alcançado através da diversificação, ou seja, investindo em diferentes tipos de ativos, como ações, títulos, commodities e outros, de modo a reduzir a exposição a riscos específicos de cada ativo.
Uma das teorias mais conhecidas relacionadas à minimização de portfólio é a Teoria Moderna do Portfólio (Modern Portfolio Theory - MPT), desenvolvida por Harry Markowitz. Essa teoria estabelece que os investidores podem criar portfólios eficientes que maximizam o retorno esperado para um determinado nível de risco, ou minimizam o risco para um determinado nível de retorno. A MPT considera não apenas o retorno e o risco individual de cada ativo, mas também a relação entre eles e como eles interagem quando combinados em uma carteira.
Para obter um portfólio que contenha o menor nível de risco possível (variância), devemos ter como inputs:
- variância dos ativos;
- covariância dos ativos;
- pesos dos ativos que minimizem a variância do portfólio.
Em um portfólio com dois ativos, pode-se calcular a variância do portfólio com a seguinte equação:
![\[\sigma^2_{p,t} = w^2_{1,t} \times \sigma^2_{1,t} + (1 - w_{1,t})^2 \times \sigma^2_{2,t} + 2w_{1,t}(1 - w_{1,t}) \times \sigma_{12,t}\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-2367b5a053eb14be6ccbf3733fc1e329_l3.png "Rendered by QuickLaTeX.com")
Veja que na equação acima definimos cada componente com o índice 
, ou seja, estamos levando em consideração os pesos, a variância e covariância dinâmica, estes dois últimos que obtemos por meio de modelos do tipo ARCH.
Pesos ótimos
Vimos acima a equação para obter a variância do portfólio, mas como calcular os pesos ótimos que possibilitem obter a menor variância possível de todas as combinações de pesos existentes para os dois ativos?
Uma abordagem é defini-los de modo que a variância seja minimizada, a oartur de uma condição de primeira ordem:
![\[\frac{\partial \sigma^2_{p,t}}{\partial w_{1,t}} = 0\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-ed002870cf5e4d7ae8606f3e9e44f895_l3.png "Rendered by QuickLaTeX.com")
A solução será
![\[w_{1,t} = \frac{\sigma^2_{2,t} - \sigma_{12,t}}{ \sigma^2_{1,t} + \sigma^2_{2,t} - 2\sigma_{12,t}}\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-555aceb43ff77fcb51e24ec865c5658d_l3.png "Rendered by QuickLaTeX.com")
Para obter todo o código em R e Python para os exemplos abaixo, faça parte do Clube AM, o repositório de códigos da Análise Macro, contendo exercícios semanais.
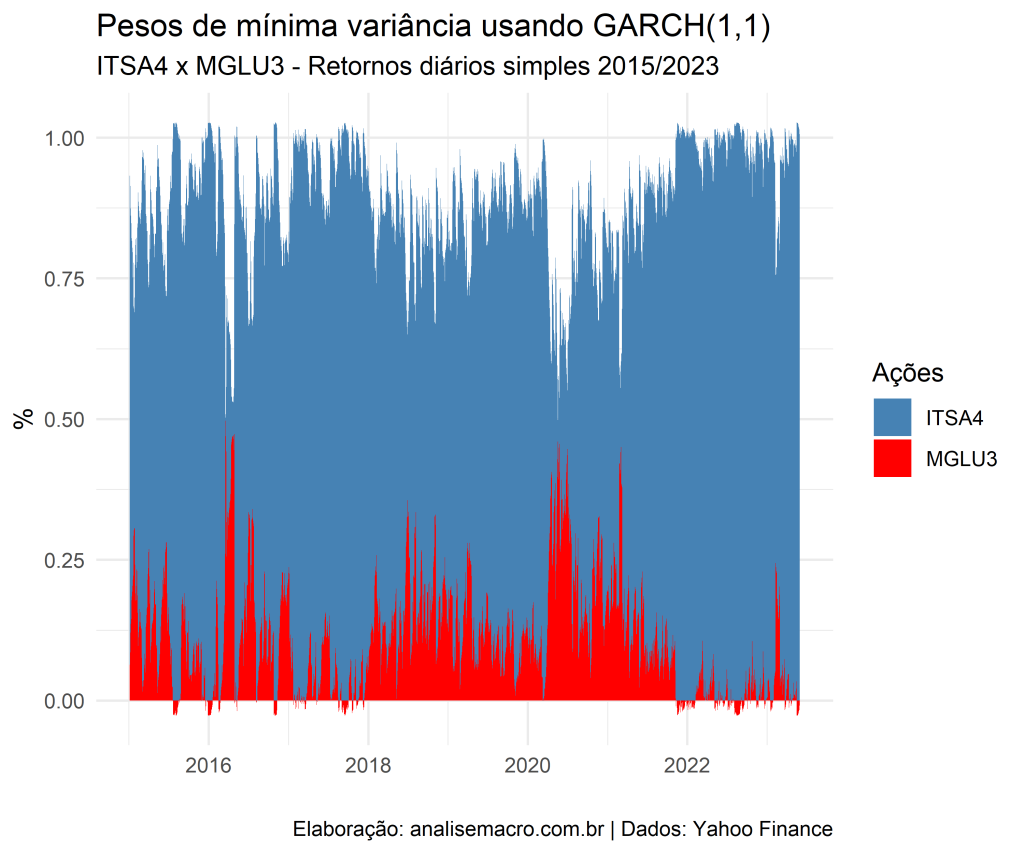
O exemplo abaixo demonstra os Pesos Dinâmicos entre ITSA4 e MGLU3, calculado a partir de um GARCH (1,1) com distribuição t de student assimétrica. Os dados referem-se ao período de 2015 a junho de 2023 em periodicidade diária com retorno simples. A estimativa foi feita tanto utilizando o R quanto o Python.
_____________________
Quer saber mais?
Veja nossa trilha de cursos de Finanças Quantitativas
