Tipos de riscos

As empresas em geral são expostas a três classes de risco: operacional, estratégico e financeiro. Os riscos financeiros são relativamente mais simples de identificar e mensurar, bem como implicam em perdas financeiras relevantes para as empresas, portanto, estaremos interessados nessa classe de risco.

Os riscos financeiros podem ser classificados, em três principais tipos:

•  Risco de mercado: é o risco da mudança do valor da posição financeira de determinado ativos/instrumento financeiro. Ocorre devido a mudanças de fatores de riscos ligados a esse determinado ativos, como por exemplo, a variação de uma ação decorrente de péssimos resultados da empresa ou mudanças no preço de títulos públicos devido a evento macroeconômicos.
•  Risco de crédito: é o risco de não receber pagamentos prometidos a empréstimos ou outros tipos de contratos, devido ao calote ou a falência do tomador.
•  Risco Operacional: o risco operacional é resultado de falhas dos processos internos de uma empresa ocasionados por pessoas, máquinas ou eventos externos.

Existem diversos outros tipos de risco financeiros, como por exemplo risco de liquidez e de subscrição, mas os três elencados são os principais avaliados nas instituição.

Como é possível compreender, os riscos referem-se tanto a eventos externos da empresa, quanto internos. Podemos portanto introduzir que o risco total de qualquer ativo é definido pela sua parte sistemática (risco sistemática) e não sistemático (risco específico ou próprio da empresa/ativo). Enquanto o primeiro é inerente a todas as empresas, o segundo é identificado como próprio do ativo, portanto, é possível reduzir esse risco diversificando o conjunto de investimentos.

Até o momento, foi-se discutido modelos para mensurar a volatilidade, entretanto, a partir da mensuração do que se conhece-se como volatilidade estatística, é possível obter uma medida que estime a perda monetária máxima em determinado número de dias, conhecido como Valor em Risco, ou em inglês, Value at Risk (VaR).

O VaR será uma medida de risco financeiro de mercado e que dará uma medida do grau de incerteza sobre retornos líquidos futuros.

Para obter todo o código em R e Python para os exemplos abaixo, faça parte do Clube AM, o repositório de códigos da Análise Macro, contendo exercícios semanais.

VaR (Value at Risk)

Informalmente, o VaR é uma medida da variação potencial máxima do valor de um ativo (ou carteira de ativos), sobre um período pré-fixado, com dada probabilidade. Ou seja, quanto se pode perder, com probabilidade , sobre um horizonte fixado.

Do ponto de vista de uma empresa, o VaR é uma medida de perda associada a um evento extremo, sob condições normais de mercado. Podemos trabalhar com um VaR paramétrico (onde assumimos uma distribuição teórica, usualmente a normal) ou um VaR empírico, em que utiliza-se os quantis empíricos.

Exemplo

Suponha que exista uma chance de 95% de que a taxa de câmbio Real/USD não caia mais do que 1% em um dia. Suponha, ainda, que uma empresa tenha 100 milhões de reais aplicados num fundo cambial.

Suponha que exista uma chance de 95% de que a taxa de câmbio Real/USD não caia mais do que 1% em um dia. Suponha, ainda, que uma empresa tenha 100 milhões de reais aplicados num fundo cambial.

Calculemos a perda potencial sobre este valor aplicado. Uma série temporal do desvio padrão (volatilidade) dos retornos da taxa de câmbio Real/USD pode dar uma indicação da variação da taxa. Vamos admitir que os retornos siga uma distribuição normal.

Suponha que uma estimativa do desvio padrão hoje seja . Então o VaR é calculado como:

Portanto, não se espera que a taxa de câmbio caia mais do que 0,759%, com 95% de probabilidade. O valor 1 , 65 ´e o (0, 05)-quantil da N N (0, 1). Em reais, o VaR ´e o valor de mercado da posi¸c˜ao multiplicado pelo valor obtido acima, ou seja,

Risco = 100 milh˜oes ×× 0, 759% = 759.000, 00 reais.

A conclusão é que em 95% das vezes, não se perderá mais do que R$ 759.000,00 em um dia.

Um pouco mais formal, supomos que no instante t estejamos interessados em calcular o risco de uma posição financeira para o horizonte h \> 0. Seja

a variação do valor do ativo entre os dois instantes. A quantidade representa o lucro ou a perda (L & P) da posição sobre o horizonte h.

Chamemos de F h(··) a função de distribuição acumulada (f.d.a.) de .

Definimos o VaR de uma posição comprada sobre o horizonte , com probabilidade , , por meio de

{#eq-var}

Observemos que o VaR depende de e de , ou seja, deveríamos escrever . Além disso, o valor em risco aumenta com diminuindo ou com aumentando.

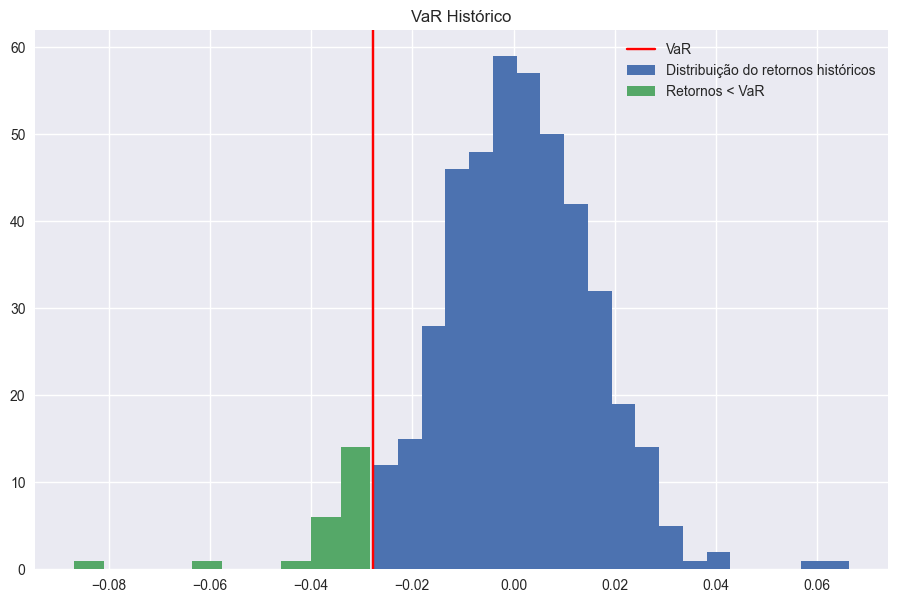
Na figura abaixo, temos a distribuição dos log-retornos de um portfólio teórico, e que representa visualmente a compreensão do VaR.

Algumas observações sobre o VaR:

(i) O VaR  é dado em unidades monetárias (u.m.), por exemplo, em reais. Lembremos que os retornos simples, , são dados em porcentagem e que os log-retornos, , são aproximadamente iguais a . Logo, podemos supor que os medem, aproximadamente, variações percentuais. Assim sendo, usaremos log-retornos no que segue.

(ii) A definição mostra que o VaR é o p-quantil da distribuição . Na prática, teremos que estimar esse quintil, usando, por exemplo, a distribuição empírica dos retornos.

(iii) O VaR calculado tem valor negativo, pois quem tem uma posição comprada sofre uma perda se .

(iv) A quantia em u.m. no cálculo do VaR é obtida como no exemplo, ou seja, multiplicando o valor da posição financeira pelo VaR do log-retorno. A posição financeira em u.m. é usualmente o valor do ativo marcado pelo mercado ("mark-to-market").

VaR com o GARCH

Lembremos que uma série de retornos é, em geral, não-correlacionada, mas dependente. Se este for o caso, a volatilidade é modelada por um modelo heteroscedásticos. Além disso, algumas séries de retornos podem exibir a presença de autocorrelação, havendo a necessidade de eliminá-la por meio do ajuste inicial de um modelo linear, por exemplo da família ARMA.

A estratégia, portanto, modelar a média da série de retornos por meio de um modelo ARMA e depois modelar os resíduos deste modelo por um membro da família ARCH.

onde e são as previsões a um passo da média e variância usando os modelos respectivos. Supondo-se, por exemplo, p = 0, 05,

Basicamente, teremos um valor do VaR ao longo do tempo, em que calculamos a medida conforme os passos de previsão da média e volatilidade.

Exemplo de VaR estimado com GARCH

Python

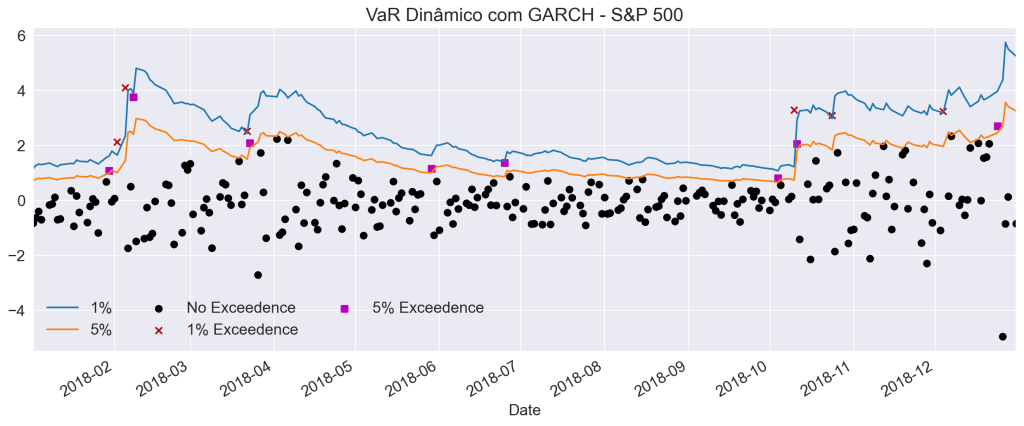
O gráfico abaixo representa os pontos que excederam a linha do VaR (x vermelho em 1% e quadrado rosa 5%) , com base na distribuição dos valores estimado pelo GARCH de dados do S&P 500

_____________________

Quer aprender mais?

Clique aqui para fazer seu cadastro no Boletim AM e baixar o código que produziu este exercício, além de receber novos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas diretamente em seu e-mail.

Referências