Volatilidade implícita é um conceito usado na análise de opções financeiras que se refere à estimativa da volatilidade futura do preço de um ativo subjacente, implícita no preço atual das opções desse ativo. No post de hoje, veremos como estimar essa medida utilizando como exemplo as opções da VALE3 no R.

Opções

Uma opção financeira é um contrato que dá ao seu titular o direito, mas não a obrigação, de comprar ou vender um ativo financeiro a um preço específico em uma data futura, ou antes dela. O ativo subjacente pode ser uma ação, um índice, uma commodity, uma moeda ou qualquer outro ativo financeiro.

Existem dois tipos principais de opções: as opções de compra (call options) e as opções de venda (put options). Uma opção de compra dá ao seu titular o direito de comprar o ativo subjacente a um preço específico (preço de exercício) em uma data futura, enquanto uma opção de venda dá ao seu titular o direito de vender o ativo subjacente a um preço específico em uma data futura.

As opções financeiras são amplamente utilizadas pelos investidores e traders no mercado financeiro como uma forma de proteger suas posições, especular sobre a direção futura do mercado ou gerar receitas adicionais a partir de seus investimentos.

Uma das maiores dúvidas dos investidores em relação as opções é como poder precificar esses tipos de instrumentos, ou seja, determinar o seu preço. O preço de uma opção é determinado por vários fatores, incluindo o preço atual do ativo subjacente, o preço de exercício da opção, o tempo restante até a expiração da opção, a volatilidade do ativo subjacente e a taxa livre de risco.

Mas como obter o preço? Isso é somente possível de posse de um modelo que possa nos auxiliar na determinação dos fatores.

Black-Scholes

O modelo de Black-Scholes é um modelo matemático utilizado para precificar opções financeiras. O modelo foi desenvolvido pelos matemáticos Fischer Black e Myron Scholes, em colaboração com Robert Merton, em 1973.

O modelo de Black-Scholes utiliza uma equação diferencial parcial para determinar o preço justo de uma opção, levando em consideração fatores como o preço atual do ativo subjacente, a volatilidade do ativo, o tempo até a expiração da opção, a taxa livre de risco e o preço de exercício da opção.

O modelo tornou-se uma ferramenta importante para investidores e traders no mercado financeiro, pois permite avaliar o preço justo de uma opção e, consequentemente, ajuda a tomar decisões de investimento mais informadas.

Como dito, o preço da opção pode ser obtido por meio de fatores: preço atual do ativo subjacente, o preço de exercício da opção, o tempo restante até a expiração da opção, a volatilidade do ativo subjacente e a taxa livre de risco. É possível perceber que esses fatores podem ser obtidos por meio de dados, exceto a volatilidade do ativo subjacente. Chamamos essa volatilidade de volatilidade implícita.

Volatilidade Implícita

A volatilidade implícita é uma medida da volatilidade futura esperada de um ativo subjacente, como uma ação, índice ou commodity, que é inferida do preço atual de uma opção sobre esse ativo. Ela é chamada de "implícita" porque é calculada a partir do preço atual de mercado da opção, em vez de ser uma medida direta da volatilidade histórica do ativo subjacente.

Quando a volatilidade implícita aumenta, o preço da opção tende a aumentar, tudo o mais constante. Isso ocorre porque um aumento na volatilidade implícita aumenta a probabilidade de que o preço do ativo subjacente se mova significativamente e, portanto, aumenta o potencial de lucro ou perda da opção.

A volatilidade implícita é importante porque é um dos principais fatores que determinam o preço de uma opção. Ela é usada no modelo de Black-Scholes e em outros modelos de precificação de opções para calcular o preço justo da opção. Em geral, quanto maior a volatilidade implícita, maior o preço da opção.

Gregas

As "gregas" são medidas utilizadas em modelos de precificação de opções, como o modelo de Black-Scholes, para quantificar a sensibilidade do preço da opção a diferentes fatores. As principais gregas são:

1. Delta: mede a sensibilidade do preço da opção em relação ao preço do ativo subjacente. O delta é expresso como um número entre -1 e 1 e indica quantos centavos o preço da opção mudará para cada unidade monetária que o preço do ativo subjacente se move.
2. Gama: mede a sensibilidade do delta em relação ao preço do ativo subjacente. O gama é expresso como um número positivo e indica quantos deltas adicionais a opção ganhará para cada unidade monetária que o preço do ativo subjacente se move.
3. Theta: mede a sensibilidade do preço da opção ao passar do tempo. O theta é expresso como um valor negativo e indica quantos centavos o preço da opção perderá por dia, tudo o mais constante.
4. Vega: mede a sensibilidade do preço da opção à volatilidade implícita do ativo subjacente. O vega é expresso como um valor positivo e indica quantos centavos o preço da opção mudará para cada ponto percentual de mudança na volatilidade implícita.
5. Rho: mede a sensibilidade do preço da opção às mudanças nas taxas de juros. O rho é expresso como um valor positivo e indica quantos centavos o preço da opção mudará para cada ponto percentual de mudança na taxa de juros livre de risco.

As gregas são úteis para os investidores e traders entenderem o risco e o potencial de recompensa de suas posições em opções e para ajustar suas estratégias de negociação de acordo com as mudanças no mercado e nos fatores que afetam o preço das opções.

Dados

Os dados de opções de ativos listados na bolsa de valores brasileira podem ser obtidos facilmente por meio do pacote {rb3}, construídos por Marcelo S. Perlin e Wilson Freitas.

Mas, quais dados podemos obter a partir do pacote para o uso do modelo de Black-Scholes?

Por meio do pacote {rb3}, é possível capturar dados do preço de ações listadas na bolsa de valores; dados referentes aos seus contrato de opções (data de referência, tipo de contrato, strike, data de maturidade, volume e contratos transacionados); e dados referentes a taxa de juros (DI X Pre; Cupom Limpo, DI x IPCA).

Portanto, é possível perceber que fica fácil construir a precificação das opções por meio do modelo de Black-Scholes, visto que podemos obter os dados facilmente.

Mas, como implementar o modelo? Podemos usá-lo facilmente por meio do pacote {oplib} criado por Wilson Freitas, disponível somente no Github. A partir do pacote, conseguimos implementar não somente o cálculo da volatilidade implícita, como também das gregas.

Exemplo

Como exemplo, podemos pegar os dados dos contratos de opções da VALE3 de 2023 usando o pacote {rb3}. Além disso, capturamos os dados da curva DI x PRE como variável de taxa de juros. Com os dados em mãos, é possível construir facilmente a Volatilidade Implicita e as gregas usando o pacote {oplib}.

A construção de todos os procedimentos para a coleta e criação dos gráficos abaixo você pode obter fazendo parte do Clube AM, o repositório especial de códigos da Análise Macro.

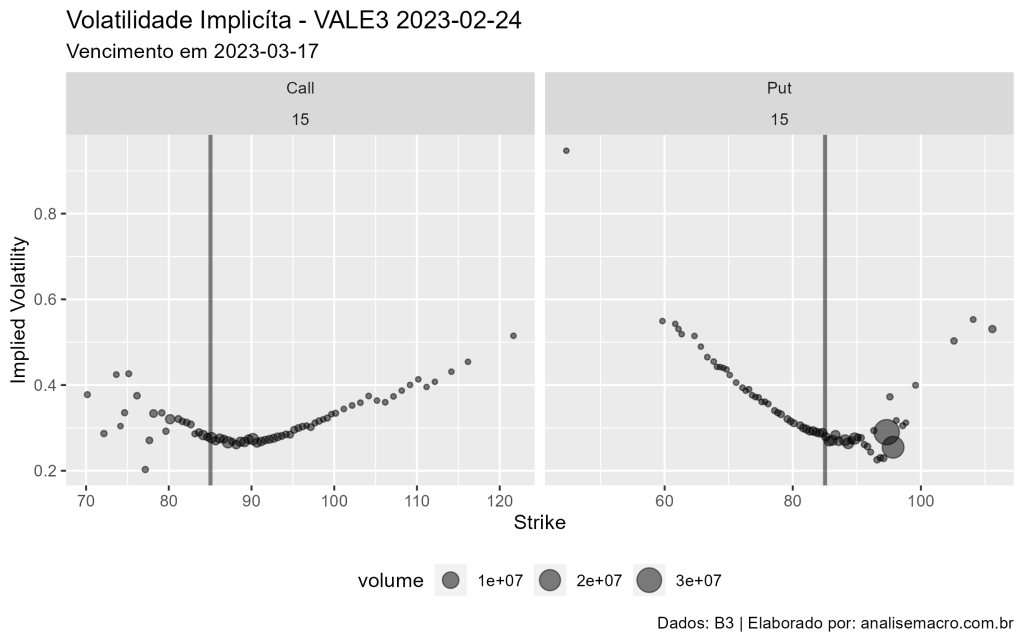
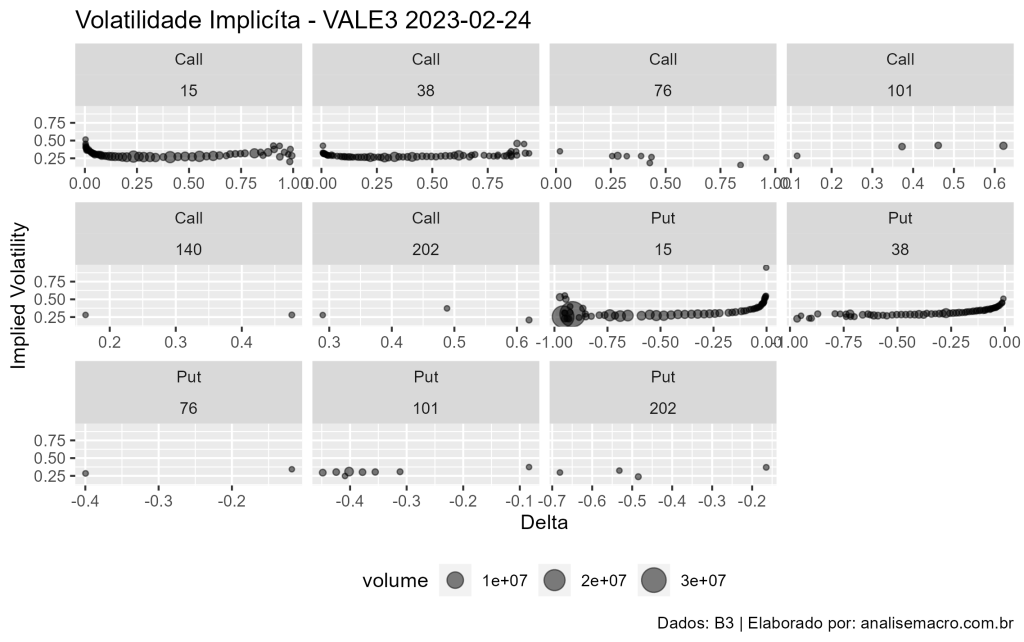
No gráfico abaixo, vemos a relação da Volatilidade Implicita x Delta de Calls e Puts da VALE3 de 2023 para diferentes maturidades, de acordo com o volume de negociação (representado pelo tamanho das "bolhas" no gráfico).

Podemos traçar uma reta vertical que representa o preço do ativo, bem como filtrar para o primeiro vencimento. Isso facilita entender o que está dentro ou fora do dinheiro para as opções.

_____________________________________

Quer saber mais?

Veja nossa trilha de cursos de Finanças Quantitativas

Referências

Freitas, W (2022). oplib: Option Volatility and Pricing Models. https://github.com/wilsonfreitas/oplib, https://wilsonfreitas.github.io/oplib/.

Freitas, W; Perlin, M (2022). Download and Parse Public Data Released by B3 Exchange.  https://github.com/ropensci/rb3, https://docs.ropensci.org/rb3/index.html

Freitas W (2023). bizdays: Business Days Calculations and Utilities.  https://github.com/wilsonfreitas/R-bizdays/, https://github.com/wilsonfreitas/R-bizdays.