Calculando o Capital Asset Pricing Model no R

O Capital Asset Pricing Model (CAPM) é um modelo, criado por Willian Sharpe, que busca estimar o retorno de um ativo baseado no retorno do mercado e na relação linear entre o ativo e o retorno do mercado. Essa relação linear é o conhecida como coeficiente beta. No post de hoje, vamos aprender a criar o CAPM Beta através do R. Os códigos de calculo fazem parte do nosso curso R para Mercado Financeiro

Para calcular o CAPM, devemos primeiro estimar o o coeficiente beta, que provem basicamente da regressão do retorno de um determinado ativo sobre o retorno do mercado. Ele captura a relação linear entre o ativo e o mercado. Para nossos propósitos, ele é uma boa forma de explorar um fluxo reprodutível para modelagem de retornos de portfólios sobre o retorno do mercado.

Para a construção do CAPM, utilizamos a seguinte equação.

Onde é

Com a equação acima, derivamos os seguintes pontos:

- O portfólio de mercado é eficiente
- O prêmio de risco de um ativo arriscado é proporcional ao seu $\beta$

É importante notar que o portfólio de mercado que gera o CAPM é muitas vezes não-observável, logo a aplicabilidade empírica do modelo pode ser limitada.

Para realizar o calcula do CAPM, utilizaremos os seguintes pacotes.

library(tidyverse)
library(tidyquant)
library(timetk)
library(broom)

Como de praxe, devemos primeiro ter nossos dados em mãos. Utilizaremos os preços de 4 ações brasileiras, bem como os dados do Ibovespa, e calculamos seus retornos mensais para criarmos nosso modelo.

# Define os ativos que irão ser coletados ------

tickers <- c("PETR4.SA", "ITUB4.SA", "ABEV3.SA", "JBSS3.SA")

# Define a data de início da coleta

start <- as.Date("2013-12-01")

# Realiza a coleta dos preços diários

prices <- getSymbols(tickers,
auto.assign = TRUE,
warnings = FALSE,
from = start,
src = "yahoo") %>%
map(~Ad(get(.))) %>%
reduce(merge) %>%
`colnames<-`(tickers)

# Transfroma os preços diários em mensais

prices_monthly <- to.monthly(prices,
indexAt = "lastof",
OHLC = FALSE)

# Calcula os retornos mensais

asset_returns <- Return.calculate(prices_monthly,
method = "log") %>%
na.omit()

# Coleta o portfólio de mercado (Ibovespa) ----

ibov <-
getSymbols('^BVSP',
from = start,
auto.assign = TRUE,
warnings = FALSE,
src = 'yahoo',)

# Transforma os dados em mensais e em retornos

ibov_returns <-
BVSP$BVSP.Adjusted %>%
`colnames<-`('BVSP') %>%
to.monthly(indexAt = 'lastof', OHLC = FALSE) %>%
Return.calculate(method = "log") %>%
na.omit()

Após o calculo dos retornos, podemos calcular o coeficiente Beta com a função CAPM.beta do pacote {PerformanceAnalytics}. A função utilziar três argumentos, sendo eles os retornos dos ativos, o retorno do portfólio de mercado e o retorno do ativo livre de risco. Nesse exercício, utilizaremos um retorno livre de risco igual a zero.

# Calcula o Beta dos ativos

CAPM.beta(Ra = asset_returns, Rb = ibov_returns, Rf = 0)

Por fim, podemos calcular um portfólio com base nos ativos que temos em mãos e podemos também calcular o CAPM para essa carteira.

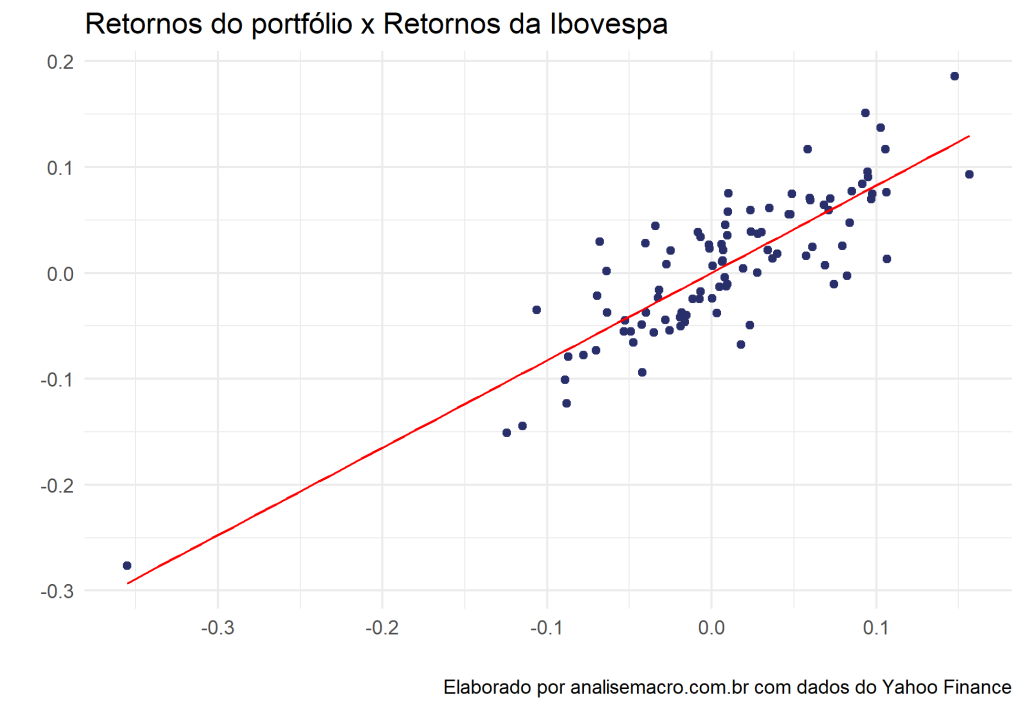
# Calcula o retorno do portfolio

portfolio_return <- Return.portfolio(asset_returns)

# Transforma em tibble

portfolio_return_tbl <- portfolio_return %>%
tk_tbl(preserve_index = TRUE,
rename_index = "date")

# Transforma o retorno do ibovespa em tibble

ibov_returns_tbl <- ibov_returns %>%
tk_tbl(preserve_index = TRUE,
rename_index = "date") %>%
rename(ibov_return = BVSP)

# Plota o gráfico de dispersão

portfolio_return_tbl %>%
left_join(ibov_returns_tbl, by = "date") %>%
ggplot(aes(x = ibov_returns, y = portfolio.returns))+
geom_point(color = "#282f6b")+
geom_smooth(method = "lm",
se = FALSE,
color = "red",
size = .5)+
labs(title = "Retornos do portfólio x Retornos da Ibovespa",
x = "",
y = "",
caption = "Elaborado por analisemacro.com.br com dados do Yahoo Finance")+
theme_minimal()

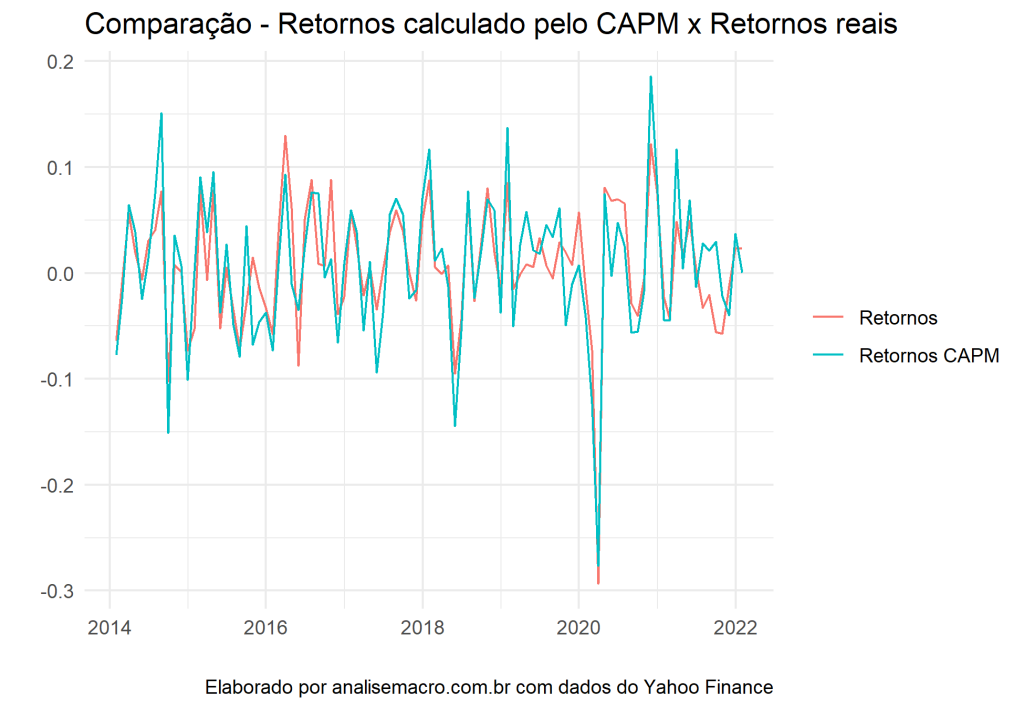
Comparamos os retornos do nosso modelo, criado a partir do CAPM, com os retornos reais.

# Cria o modelo com os valores "fittados"

portfolio_model <-
portfolio_return_tbl %>%
lm(portfolio.returns ~ ibov_returns_tbl$ibov_return, data = .) %>%
augment() %>%
mutate(date = portfolio_return_tbl$date)

# Compara o modelo com o retornos reais

portfolio_model %>%
ggplot(aes(x = date))+
geom_line(aes(y = .fitted,
color = "Retornos"))+
geom_line(aes(y = portfolio.returns,
color = "Retornos CAPM"))+
labs(title = "Comparação - Retornos calculado pelo CAPM x Retornos reais",
x = "",
y = "",
caption = "Elaborado por analisemacro.com.br com dados do Yahoo Finance")+
theme_minimal()+
theme(legend.title = element_blank())

________________________

(*) Para entender mais sobre Mercado Financeiro, seleção de carteira e a Teoria de Markowitz, confira nosso curso de R para o Mercado Financeiro.
________________________