Os retornos de um investimento apresentam diversas propriedades estatísticas que podem ser avaliadas empiricamente, e que são extremamente necessárias para a estimação de modelos de séries temporais. No post de hoje, vamos realizar uma análise exploratória da série de retornos diária do Ibovespa utilizando o Python.

Retorno de um Investimento

Um retorno de investimento representa a variação relativa do preços de um ativo financeiros em determinado período, e podem ser calculados como, pelo o que chama-se de retorno líquido simples como:

Fatos Estilizados

O interessante é que possuem propriedades estatísticas que são avaliadas empiricamente pelo o que chama-se de fatos estilizados.

Os fatos estilizados referem a característica empírica presente em uma variedade grande de ativos, mercados e períodos e consistente entre todos e são obtidos separando os denominadores comuns entre as propriedades observadas nos estudos de diferentes mercados e ativos e que são usualmente explicados principalmente pela volatilidade dos ativos.

Vamos analisar os principais fatos estilizados dos retornos usando principalmente gráficos e estatísticas descritivas.

Os principais fatos estilizados relativos a retornos financeiros podem ser resumidos:

1. retornos em geral não são autocorrelacionados;
2. os quadrados dos retornos são autocorrelacionados
3. séries de retornos apresentam agrupamentos de volatilidades ao longo do tempo
4. a distribuição dos retornos apresenta caudas mais pesadas do que uma distribuição normal, bem como, apesar de a distribuição apresentar-se simétrica, é, em geral,  leptocúrtica.

Vamos averiguar cada ponto dessa questão tomando como exemplo os retornos do índice bovespa. Abaixo, utilizamos o pandas_datareader e o yfinance para buscar os dados do preço de fechamento da Ibovespa e calcular o retorno líquido simples.

Todo o código criado no Python,  que possibilita criar os gráficos abaixo, você pode obter através do Clube AM, o repositório especial da Análise Macro, no qual compartilhamos códigos de R e Python comentados com vídeo aulas.

import pandas as pd
import numpy as np
import pandas_datareader.data as pdr
from matplotlib import pyplot as plt
import seaborn as sns
sns.set()
!pip install yfinance --upgrade --no-cache-dir
import yfinance as yf
yf.pdr_override()

symbols = ['^BVSP']
inicio = '2010-01-01'
fim = '2022-12-01'
precos = pdr.get_data_yahoo(symbols, start = inicio, end = fim)[['Close']]
retornos = precos.pct_change().dropna()

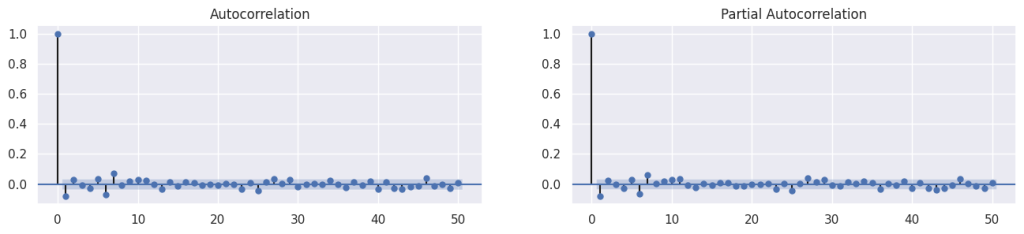
1 - Autocorrelação dos retornos

Os retornos de fato não podem ser explicados por seus valores passados. Isso pode ser evidenciado ao analisar os gráficos de autocorrelação e autocorrelação parcial da série de retornos diários do Ibovespa.

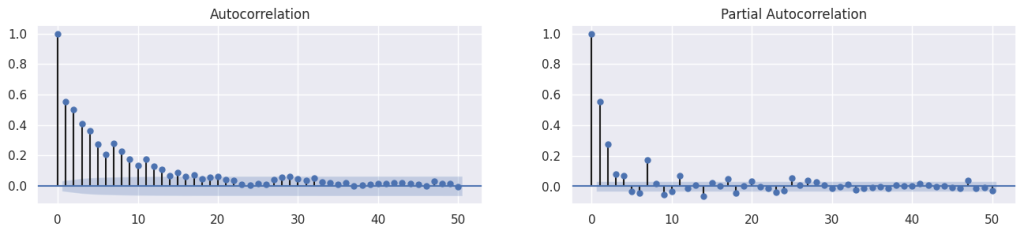
2 - Autocorrelação dos quadrados dos retornos

Apesar da série dos retornos não poder ser explicada por seus valores passados, temos uma situação diferente para o caso dos retornos ao quadrados. Na prática, essa relação exibe que se tomaremos o pressuposto de que os retornos esperados da série diária dos retornos é suficiente próxima de zero, isso torna que os retornos ao quadrado são na realidade

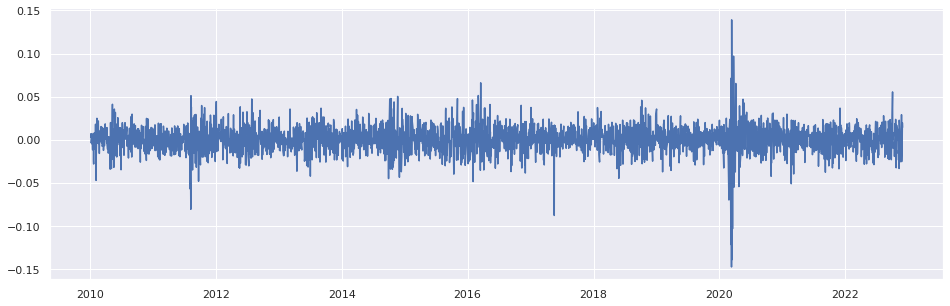
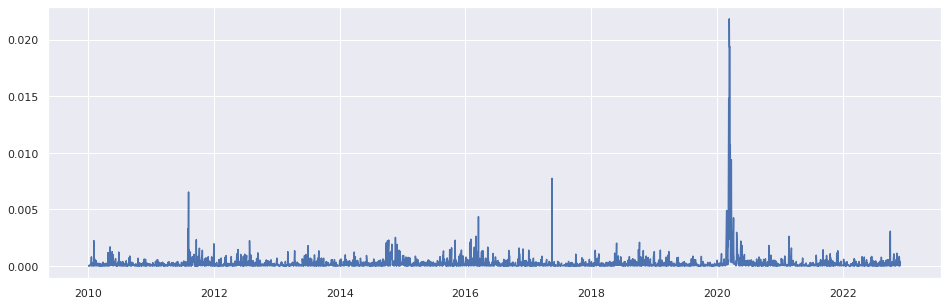
3 - Séries de retornos apresentam agrupamentos de volatilidades ao longo do tempo

Essa questão é fácil de averiguar por meio do gráfico da série temporal dos retornos diários. Veja que os valores sempre estão em torno de zero, entretanto, com períodos de maiores e menores variações. Esse agrupamento de volatilidade são chamados de Volatility Clusters.

Essa questão fica evidente ao utilizarmos os retornos ao quadrado

4 - A distribuição dos retornos apresenta caudas pesadas e leptocúrtica

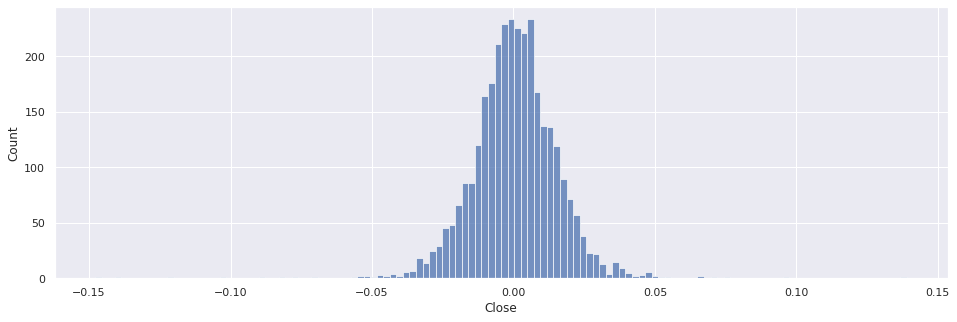
É possível averiguar essa situação visualizando o histograma da série de retornos, no qual representa frequência das observações. Fica claro que apesar de se assemelhar a uma distribuição normal, ela é leptocúrtica, ou seja, é mais pontiaguda e caudas longas.

Portanto, na amostra acima, obteve-se uma curtose de valor 9.97 e assimetria de -0.50.

______________________________________

Quer saber mais?

Veja nosso curso de Python para Investimentos.