O que é o vectorbt?
VectorBT é uma biblioteca Python de código aberto para análise quantitativa e backtesting. O intuito da biblioteca é auxiliar na construção de trading algorítmico e na realização de backtesting de estratégias de investimento. Realizamos uma introdução a biblioteca conforme o post "Primeiros Passos com o vectorbt".
Como criar um Portfólio de Investimentos?
Um portfólio de investimentos refere-se a uma coleção de ativos financeiros, como ações, títulos, fundos mútuos, imóveis e outros instrumentos financeiros, detidos por um investidor. O objetivo principal de construir um portfólio é diversificar os investimentos para reduzir o risco total. A diversificação permite que os investidores alcancem um equilíbrio entre risco e retorno, pois diferentes ativos reagem de maneira diferente às mudanças do mercado.
Assim sendo, criar um portfólio de investimentos reside na gestão eficaz do risco e na busca de retornos ajustados ao risco. Ao diversificar os investimentos em várias classes de ativos, setores e regiões geográficas, os investidores podem reduzir a exposição a eventos adversos específicos e aumentar as chances de obter retornos consistentes ao longo do tempo. Além disso, a construção de um portfólio alinhado aos objetivos financeiros e ao perfil de risco do investidor ajuda a alcançar metas específicas.
O cálculo do retorno de um portfólio envolve a ponderação dos retornos individuais de cada ativo pelo seu peso no portfólio. A fórmula básica para calcular o retorno de um portfólio ponderado é:
Onde:
- são os pesos dos ativos no portfólio (expressos como porcentagens do valor total do portfólio).
- são os retornos dos ativos individuais.
Por exemplo, se um investidor possui 50% de seu portfólio em ações com um retorno de 10% e 50% em títulos com um retorno de 5%, o retorno do portfólio seria:
*** QuickLaTeX cannot compile formula:
(0,5 \times 0,10) + (0,5 \times 0,05) = 0,075 \text{ ou 7,5%}
*** Error message:
File ended while scanning use of \text@.
Emergency stop.
É importante notar que esse cálculo é uma simplificação, pois não considera outros fatores como custos, impostos e o efeito de rebalanceamento do portfólio ao longo do tempo.
O que iremos criar?
Usando o vectorbt, iremos realizar a construção de 2000 Portfólio de Investimentos simulados, com base em 4 ativos escolhidos de forma aleatória (apenas para exemplificar o exercício). São eles: ITSA4, WEGE3, VALE3 e PETR4.
O período da amostra segue de 2019 até fim de 2023.
A ideia é gerar 8000 pesos aleatórios diferentes dos ativos e realizar a construção de 2000 Portfólio. Iremos escolher o Portfólio que melhor performou baseado em uma medida de risco-retorno (Índice de Sharpe). Ao fim, verificamos as principais estatísticas do Portfólio.
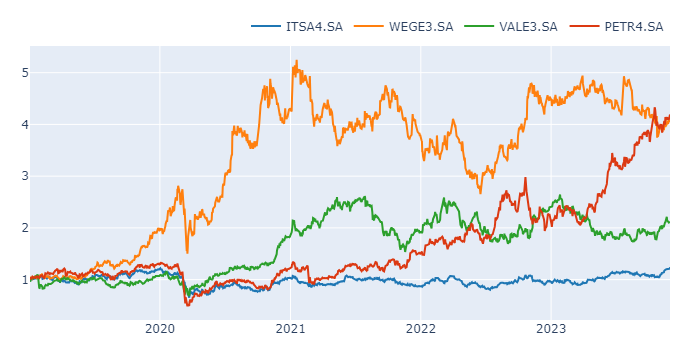
Abaixo, construímos com o vectorbt, o preço normalizado (retorno bruto acumulado) dos ativos individuais.
Verificamos as principais estatísticas descritivas de cada ativo.
Vemos que a média do retorno diário do ativo PETR4 performou melhor que os seus pares, enquanto a ITSA4 teve o pior desempenho.
Código
symbol
ITSA4.SA 0.034657
WEGE3.SA 0.144166
VALE3.SA 0.094184
PETR4.SA 0.159173
dtype: float64 Em relação a volatilidade, verificamos que a PETR4 foi a mais arriscada, enquanto ITSA4 a que possuiu menor desvio padrão.Código
symbol
ITSA4.SA 1.852222
WEGE3.SA 2.412038
VALE3.SA 2.549426
PETR4.SA 2.845702
dtype: float64 A matriz de correlação demonstra que os ativos são todos positivamente correlacionados, indicando uma trajetória comum de seus retornos.Código
| symbol | ITSA4.SA | WEGE3.SA | VALE3.SA | PETR4.SA |
|---|---|---|---|---|
| symbol | ||||
| ITSA4.SA | 1.000000 | 0.375203 | 0.365221 | 0.555038 |
| WEGE3.SA | 0.375203 | 1.000000 | 0.251787 | 0.338850 |
| VALE3.SA | 0.365221 | 0.251787 | 1.000000 | 0.466736 |
| PETR4.SA | 0.555038 | 0.338850 | 0.466736 | 1.000000 |
Criando o Portfólio com alocação em um único tempo
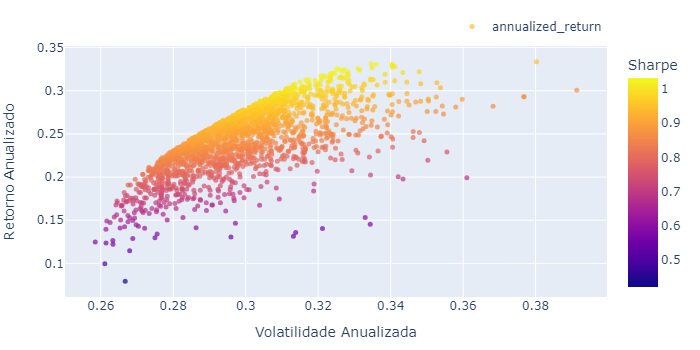
Simulamos os 2000 Portfólios, e verificamos os resultados em um gráfico de dispersão que demonstra a relação de retorno anualizado x risco anualizado. As cores são construídas conforme o Índice de Sharpe.
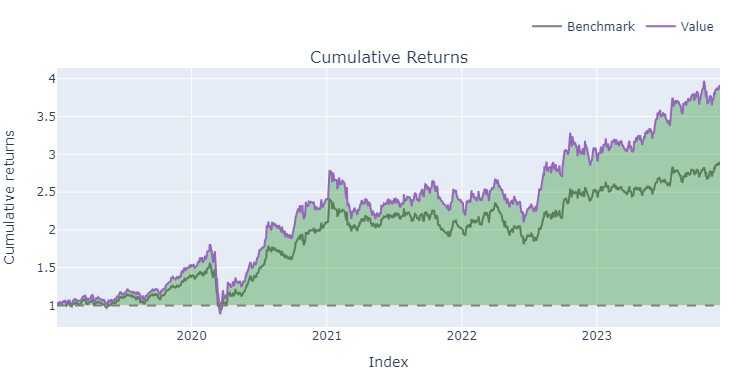
Escolhemos o melhor Portfólio, conforme o melhor Índice de Sharpe e verificamos os resultados abaixo.
Pesos dos ativos (em sequência):
Código
array([0.00721164, 0.36543672, 0.09805157, 0.52930007])Código
Start 2019-01-02 02:00:00+00:00
End 2023-11-30 03:00:00+00:00
Period 1222 days 00:00:00
Start Value 100.0
End Value 392.031083
Total Return [%] 292.031083
Benchmark Return [%] 190.328172
Max Gross Exposure [%] 100.0
Total Fees Paid 0.0
Max Drawdown [%] 51.129977
Max Drawdown Duration 396 days 00:00:00
Total Trades 4
Total Closed Trades 0
Total Open Trades 4
Open Trade PnL 292.031083
Win Rate [%] NaN
Best Trade [%] NaN
Worst Trade [%] NaN
Avg Winning Trade [%] NaN
Avg Losing Trade [%] NaN
Avg Winning Trade Duration NaT
Avg Losing Trade Duration NaT
Profit Factor NaN
Expectancy NaN
Sharpe Ratio 1.03282
Calmar Ratio 0.63646
Omega Ratio 1.211264
Sortino Ratio 1.431265
Name: 210, dtype: objectCódigo
Retorno Total: 292.03%
Drawdown Máximo: -51.13%Código
Performance Individual dos ativos weights symbol_group symbol 0.007212 210 ITSA4.SA 0.171749 0.365437 210 WEGE3.SA 112.037095 0.098052 210 VALE3.SA 10.972734 0.529300 210 PETR4.SA 168.849505 Name: total_return, dtype: float64
Quer aprender mais?
Clique aqui para fazer seu cadastro no Boletim AM e baixar o código que produziu este exercício, além de receber novos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas diretamente em seu e-mail.