Introdução
Montar uma carteira de ações eficiente — que maximize retorno e minimize risco — é um dos principais desafios enfrentados por investidores, gestores e analistas de investimentos. A tomada de decisão nessa área vai muito além de escolher os ativos “da moda” ou seguir dicas de especialistas: ela envolve um processo estruturado, quantitativo e orientado por dados.A literatura financeira clássica divide esse processo em três grandes etapas:
- Análise dos títulos (entender o comportamento individual de cada ativo);
- Análise das carteiras (como diferentes combinações afetam risco e retorno);
- Seleção da carteira ótima, de acordo com objetivos e tolerância ao risco.
Neste post, vamos focar na terceira etapa — a seleção da carteira — utilizando uma das ferramentas mais consagradas da teoria moderna das finanças: o modelo de média-variância de Harry Markowitz, também conhecido como modelo de otimização de portfólio. Nosso objetivo será mostrar, passo a passo, como implementar esse modelo em Python. A ideia é transformar teoria em prática, utilizando dados reais do mercado para construir uma carteira eficiente, calcular fronteiras de risco e retorno e identificar alocações ideais para diferentes perfis de investidor.
Para obter o código e o tutorial deste exercício faça parte do Clube AM e receba toda semana os códigos em R/Python, vídeos, tutoriais e suporte completo para dúvidas.
Para implementar a otimização de carteiras segundo o modelo de Markowitz, utilizaremos a biblioteca Riskfolio-Lib, uma das ferramentas mais completas em Python para análise e otimização de portfólios. Essa biblioteca oferece uma ampla gama de métodos, incluindo otimizações baseadas em média-variância, medidas de risco alternativas (como CVaR e MAD), além de funcionalidades avançadas para geração de gráficos, simulações e análise de desempenho.
Com ela, é possível automatizar desde a construção da fronteira eficiente até a escolha da carteira ótima com base em diferentes perfis de risco, tornando o processo robusto e visualmente interpretável.
Conjunto de Dados
Como exemplo prático, vamos construir uma carteira com ações de quatro empresas brasileiras negociadas na B3:
- BBDC4.SA (Banco Bradesco)
- ITSA4.SA (Itaúsa)
- GGBR4.SA (Gerdau)
- WEGE3.SA (Weg)
O período considerado será de janeiro de 2016 a dezembro de 2022, e os dados utilizados serão os preços de fechamento mensais. A coleta será feita diretamente da API do Yahoo Finance, utilizando a biblioteca yfinance, que facilita o acesso a séries históricas de ativos financeiros de forma gratuita e eficiente. Abaixo, a tabela exibe os retornos históricos do nosso conjunto de dados (primeiras 5 observações).
| BBDC4.SA | ITSA4.SA | GGBR4.SA | WEGE3.SA | |
|---|---|---|---|---|
| Date | ||||
| 2016-02-01 | 17.6933% | -1.9444% | -0.8721% | -14.6831% |
| 2016-03-01 | 26.9335% | 85.2691% | 23.1362% | 7.1198% |
| 2016-04-01 | 5.3757% | 19.4190% | 6.2302% | 8.4479% |
| 2016-05-01 | -11.9086% | -28.6812% | -9.3072% | -5.2042% |
| 2016-06-01 | 10.5212% | 5.7451% | 6.3025% | -4.5170% |
Conjunto de Oportunidades
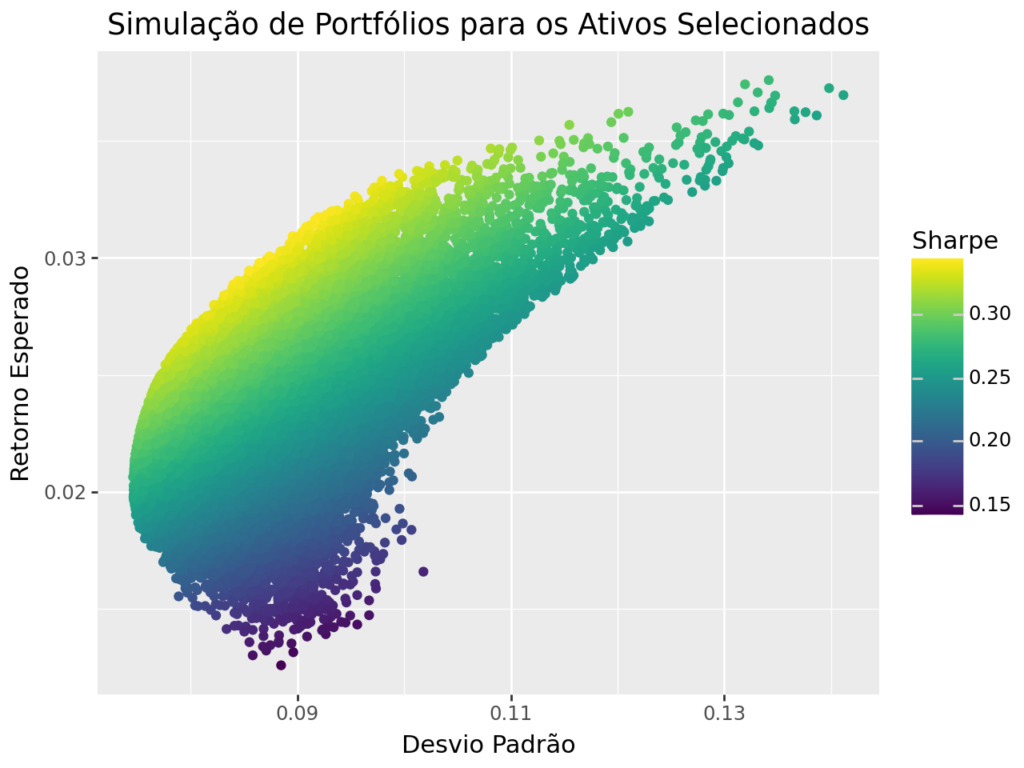
No gráfico abaixo, observamos o que acontece com o risco e o retorno ao combinarmos diferentes ativos. Esse gráfico é conhecido como o Conjunto de Oportunidades de Investimento — ele representa todas as combinações possíveis de pesos entre os ativos, mapeadas no plano risco x retorno.
O objetivo da seleção de carteiras é identificar a melhor combinação possível de ativos, considerando as preferências do investidor em relação ao risco e ao retorno esperados. Dentre todas as carteiras que podem ser formadas com os ativos disponíveis, buscamos aquela que maximiza o grau de satisfação do investidor.
Nesse contexto, consideramos como “grau de satisfação” a escolha da carteira que:
- Minimiza o risco entre todas as combinações possíveis;
- Maximiza o retorno entre todas as combinações possíveis;
- Maximiza o retorno ajustado ao risco (ex.: razão de Sharpe);
- Maximiza a utilidade esperada do investidor.
Para entender como fazer essa escolha, vamos construir o Conjunto de Oportunidades utilizando os ativos cujos dados foram coletados e os retornos simples já calculados.
A pergunta-chave aqui é: Qual combinação de portfólio devemos escolher? Ou seja, qual ponto (combinação de pesos) representado no gráfico seria mais adequado?
Essa decisão envolve certo grau de subjetividade, pois cada investidor possui um nível distinto de aversão ao risco e está disposto a aceitar mais risco em troca de retornos mais elevados.
Ainda assim, podemos recorrer ao princípio da dominância: é racional preferir combinações que ofereçam o mesmo retorno com menor risco. Se houver duas carteiras com o mesmo nível de retorno, mas riscos diferentes, escolhe-se aquela com menor risco. Da mesma forma, se o risco for o mesmo, prefere-se a carteira com maior retorno.
No gráfico criamos diversas carteiras com uma simulação de 25000 portfólios diferentes. São apenas algumas das possíveis carteiras que poderiam ser formadas com os ativos em questão.
Fronteira Eficiente
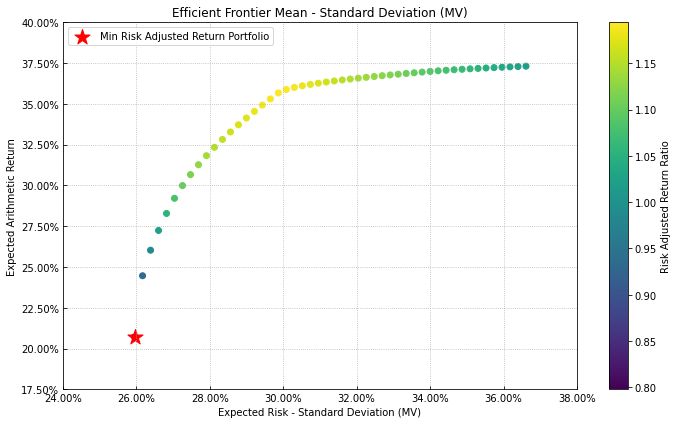
A seleção da carteira de investimento mais atraente para um investidor racional, que avalia a relação risco/retorno em suas decisões, fica restrita às combinações disponíveis no trecho da linha de combinações descrita no gráfico acima. Esse segmento, conhecido por fronteira eficiente, insere todas as carteiras possíveis de serem construídas.
A fronteira eficiente restringe o conjunto de oportunidades para somente poucos títulos.
Isso porque o investidor racional deverá escolher aquela combinação que maximiza o retorno esperado para um menor nível possível de risco ou, em outras palavras, a que promove o menor risco para um dado retorno esperado. As alternativas de investimento que atendem a essa orientação são aquelas dispostas ao longo da linha vermelha tracejada, e são denominadas por Markowitz de eficientes.
A escolha da melhor carteira é determinada, uma vez mais, pela postura demonstrada pelo investidor em relação ao dilema risco/retorno presente na avaliação de investimentos.
A partir da Fronteira Eficiente só é possível aumentar o retorno aumentando o risco – compatível com a teoria clássica de finanças – por isso ela é chamada de eficiente.
Como obtemos a melhor carteira?
Vamos elencar duas formas de obtermos as melhores carteiras de investimento do nosso Conjunto de Oportunidades de forma a abarcamos as preferências do investimento. A que possuí risco mínimo e máximo retorno.
No caso em que não são permitidas vendas à descoberto e nem empréstimos, temos as seguintes restrições;
- a soma das proporções alocadas em cada ativo tem que ser igual a um;
- cada ativo tem que ter peso maior ou igual a zero;
- em cada problema escolhemos um retorno esperado para o qual minimizaremos o risco ou maximizaremos o retorno.
Carteira de Variância Mínima
Para marcar um ponto na fronteira eficiente, escolhemos um nível de retorno e resolvemos o problema de minimização de risco.
Formalmente, o problema de otimização para cada ponto do gráfico é:
![\[min_{w_i} \ \ \sum_{j=1}^N(w_j^2 \sigma_j^2)+\sum_{j=1}^N\sum_{\substack{k=1 \\ k \neq j}}^N(w_j w_k \sigma_{jk})\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-7f8c3d860084d283d558bad5d41f97a2_l3.png "Rendered by QuickLaTeX.com")
Carteira de Máximo Retorno
![\[max_{w_i} \ \ E(R_p)=\sum_{i=1}^N(w_{i}E(R_i))\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-9fe287e0183b3d5b0c7f8c9a389b61b0_l3.png "Rendered by QuickLaTeX.com")
3. Otimização de Carteira com riskfolio
Para produzir nossas carteiras ótimas, vamos fazer o uso da biblioteca riskfolio, que permite obtermos ferramentas para a construção de carteiras com a escolha de diversas medidas para:
- Retorno esperado;
- Risco;
- Restrições;
- Gráficos e tabelas;
- Entre diversas ferramentas.
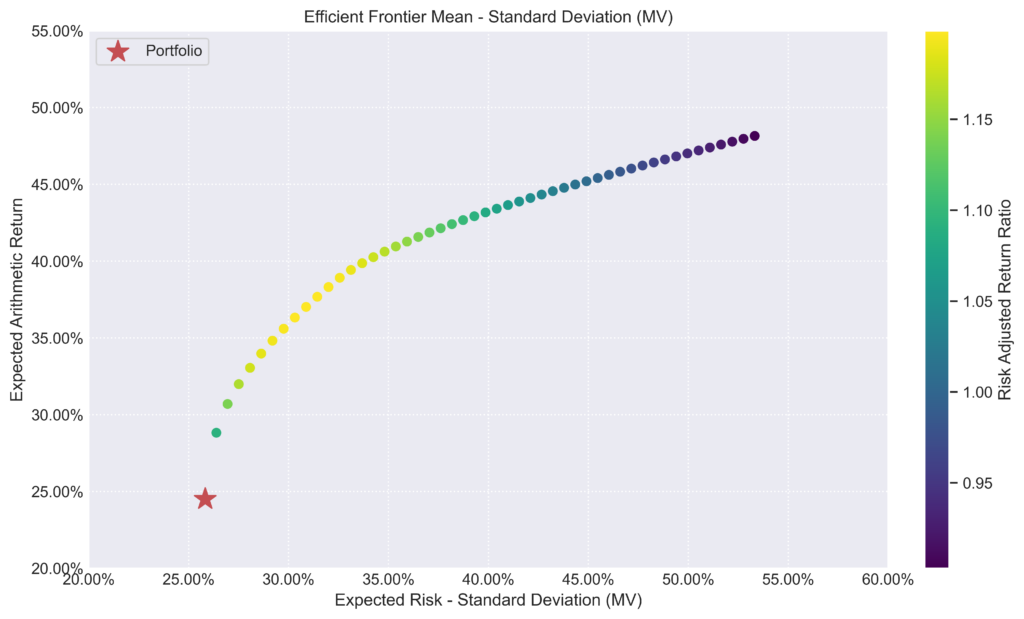
Construímos para nossa carteira de mínima variância:
Carteira de Mínima Variância
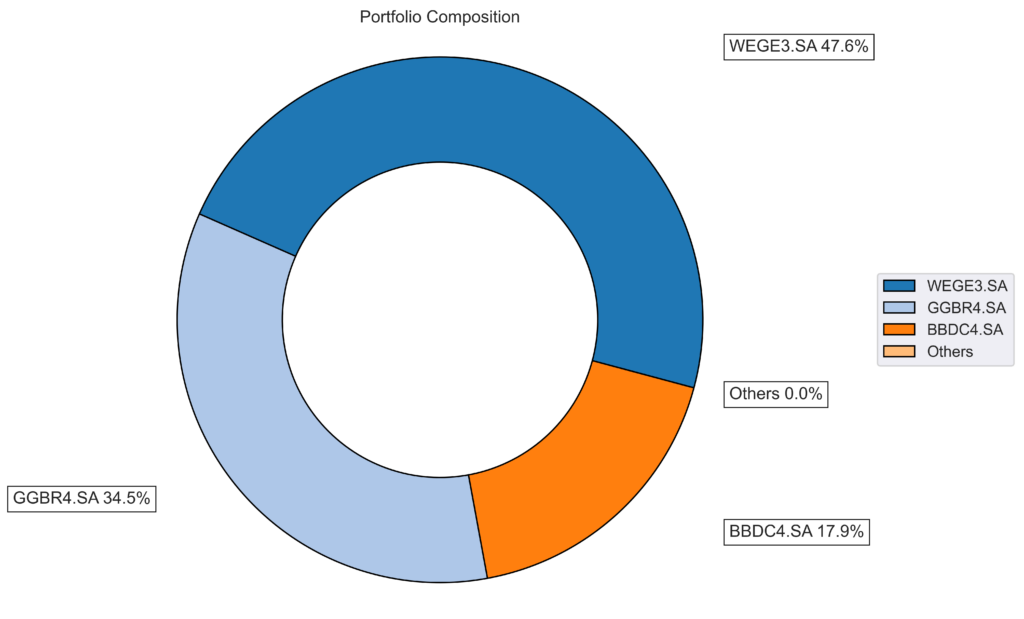
Abaixo, os pesos ótimos encontrados pelo algoritmo.
| BBDC4.SA | ITSA4.SA | GGBR4.SA | WEGE3.SA | |
|---|---|---|---|---|
| weights | 17.9431% | 0.0000% | 34.4888% | 47.5681% |
Na tabela seguinte, temos as melhores 5 combinações (valores da fronteira eficiente).
| BBDC4.SA | ITSA4.SA | GGBR4.SA | WEGE3.SA | |
|---|---|---|---|---|
| 0 | 17.9431% | 0.0000% | 34.4888% | 47.5681% |
| 1 | 36.0408% | 3.7925% | 1.5413% | 58.6255% |
| 2 | 30.5656% | 9.0142% | 0.0000% | 60.4202% |
| 3 | 25.6382% | 12.8615% | 0.0000% | 61.5002% |
| 4 | 21.5888% | 16.0172% | 0.0000% | 62.3940% |
A Fronteira Eficiente são os pontos marcado no gráfico acima, que fazem parte do Conjunto de Oportunidade de Investimento (COI) que começa na carteira de variância mínima e vai até a carteira de retorno máximo (todo investimento no ativo de maior retorno).
A carteira de variância mínima é interessante não só teoricamente (por definir o início da Fronteira), como também na prática, pois ela define a combinação de ativos que gera a carteira eficiente com menor risco.
A carteira de variância mínima é a que tem menor risco. Ela fica na extremidade esquerda do COI, onde começa a Fronteira Eficiente.
Podemos verificar também os pesos dos ativos que compõem a carteira de variância mínima.
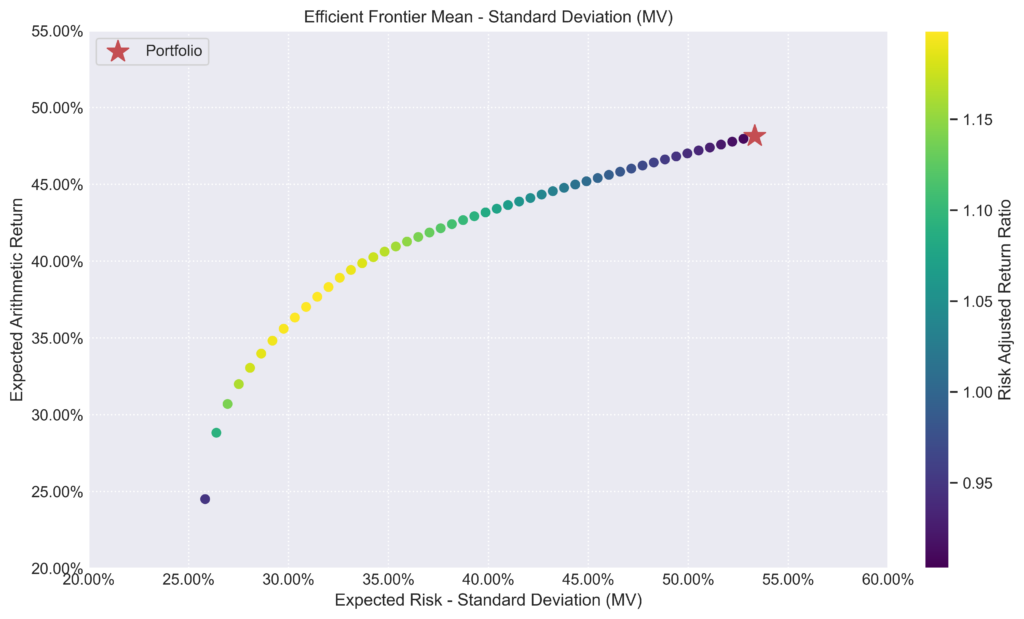
Carteira de Máximo Retorno
Vamos agora construir a carteira de máximo retorno usando a biblioteca riskfolio.
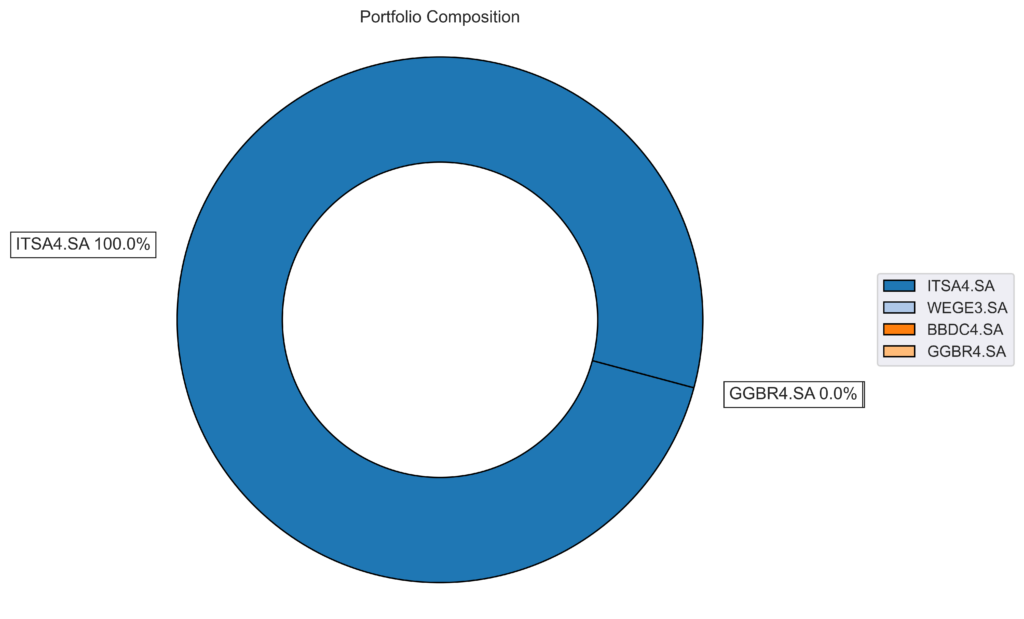
Abaixo, os pesos ótimos encontrados pelo algoritmo.
| BBDC4.SA | ITSA4.SA | GGBR4.SA | WEGE3.SA | |
|---|---|---|---|---|
| weights | 0.0000% | 100.0000% | 0.0000% | 0.0000% |
Na tabela seguinte, temos as melhores 5 combinações (valores da fronteira eficiente).
| BBDC4.SA | ITSA4.SA | GGBR4.SA | WEGE3.SA | |
|---|---|---|---|---|
| 0 | 17.9431% | 0.0000% | 34.4888% | 47.5681% |
| 1 | 36.0408% | 3.7925% | 1.5413% | 58.6255% |
| 2 | 30.5656% | 9.0142% | 0.0000% | 60.4202% |
| 3 | 25.6382% | 12.8615% | 0.0000% | 61.5002% |
| 4 | 21.5888% | 16.0172% | 0.0000% | 62.3940% |
Quer aprender mais?
Conheça nossa Formação do Zero à Análise de Dados Econômicos e Financeiros usando Python e Inteligência Artificial. Aprenda do ZERO a coletar, tratar, construir modelos e apresentar dados econômicos e financeiros com o uso de Python e IA.
Referências:
A. A. Neto. Mercado Financeiro. Editora Atlas, 2012.
E. J. Elton et al. Moderna Teoria de Carteiras e Análise de Investimentos. Editora Elsevier, 2010
PALLEJA, Danyel. Riskfolio-Lib: Portfolio Optimization and Quantitative Strategic Asset Allocation in Python. Disponível em: https://riskfolio-lib.readthedocs.io/en/latest/. Acesso em: 14 maio 2025.
