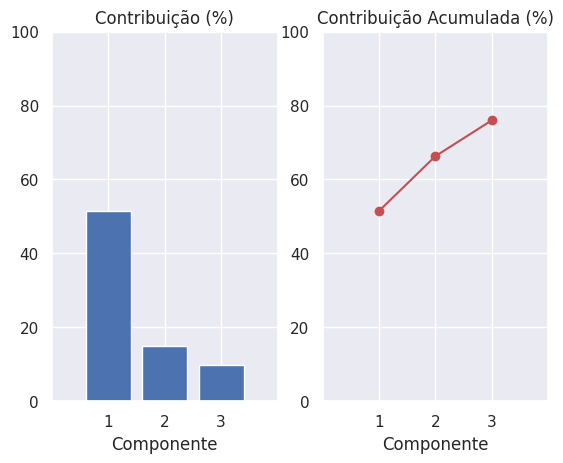
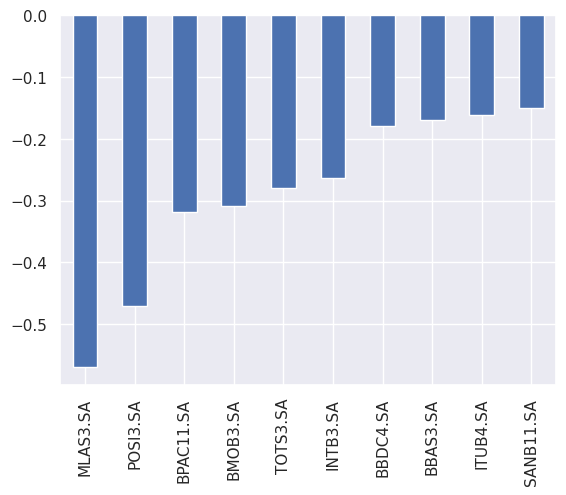
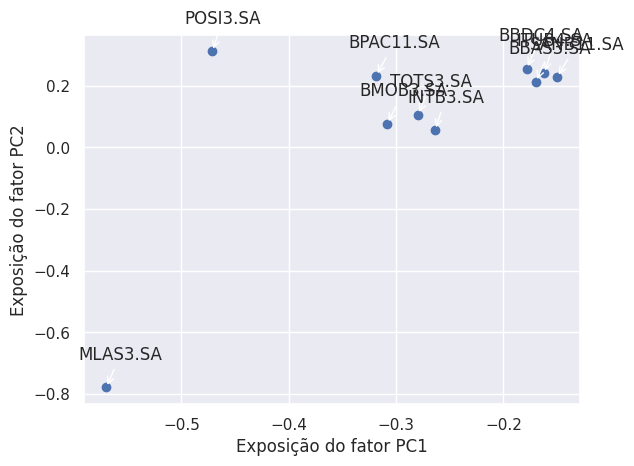
Um tópico importante na análise de séries temporais multivariadas é o estudo da estrutura de covariância (ou correlação) das séries. Por exemplo, a estrutura de covariância de uma série de retornos desempenha um papel importante na seleção de portfólio. Isto porque, dados multivariados frequentemente exibem padrões semelhantes, indicando a existência de uma estrutura comum oculta. A análise fatorial estatística é um desses métodos simplificadores disponíveis na literatura. O objetivo da análise fatorial estatística é identificar, a partir dos dados observados, alguns fatores que podem explicar a maior parte das variações na matriz de covariância ou correlação dos dados.
Como usar o PCA em análise de investimentos?
Exemplo:
Vamos utilizar como exemplo os dados da série de retornos simples diários (com dividendos) das seguintes empresas:
- 'INTB3.SA'
- 'MLAS3.SA'
- 'POSI3.SA'
- 'TOTS3.SA'
- 'BMOB3.SA'
- 'BPAC11.SA'
- 'BBDC4.SA'
- 'ITUB4.SA'
- 'BBAS3.SA'
- 'SANB11.SA'
Observe que há cinco empresas do setor de tecnologia e cinco empresas do setor bancário. O objetivo aqui é identificar quais fatores mais impactam a variabilidade dos retornos dessas ações. Além disso, vamos determinar o valor de cada fator e analisar as relações entre os fatores nas empresas.
Quer aprender mais?
- Cadastre-se gratuitamente aqui no Boletim AM e receba toda terça-feira pela manhã nossa newsletter com um compilado dos nossos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas;
- Quer ter acesso aos códigos, vídeos e scripts de R/Python desse exercício? Vire membro do Clube AM aqui e tenha acesso à nossa Comunidade de Análise de Dados;
- Quer aprender a programar em R ou Python com Cursos Aplicados e diretos ao ponto em Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas? Veja nossos Cursos aqui.