Construindo o Modelo de 3 fatores de Fama-French para o mercado brasileiro com o Python

O que é o Modelo de 3 Fatores de Fama-French e como ele é construído? Neste artigo, demonstramos como replicar esse modelo com exemplos utilizando dados do mercado financeiro brasileiro. Além disso, realizamos uma análise dos coeficientes estimados. Todo esse processo é realizado utilizando a linguagem de programação Python.

Fama e French em uma séries de artigos no início dos anos 1990, estabeleceram as bases de um modelo de índices múltiplos baseados em características da empresa.

A ideia foi verificar que além do risco de mercado geral, tanto o tamanho (capitalização de mercado) quanto a razão entre o valor contábil da ação e o seu valor de mercado têm um papel importante na determinação do retorno médio de ações.

Verificaram que os retornos médios das ações são negativamente relacionado com o tamanho e positivamente relacionado com a razão valor contábil/valor de mercado.

Em termos simples, empresas pequenas e empresas em que a razão entre o valor contábil e o valor de mercado da ação é baixo são mais arriscadas.

Como verificar a relação?

Séries de valor contábil da ação são divulgados, no máximo, quatro vezes por ano. Para testar hipóteses de séries de retornos, precisamos de um intervalo menor. Nesta condição, Fama e French formularam três índices para explicar o excesso de retorno das ações.

Como assim índices? A ideia é a criação de carteiras teóricas em que os retornos imitem o impacto das variáveis de tamanho da empresa e valor contábil/valor de mercado. Ao criar carteiras com retornos pelo menos mensais, Fama e French convertem um conjunto de variáveis que não podem ser observados em intervalos frequentes em um conjunto de ativos que podem ser observados a intervalos de tempos frequentes.

Portanto, houve a transformação de dados fundamentais de empresas em índices de retornos. Na prática essa transformação ocorreu da seguinte forma:

SMB (Small minus Big)

Classificação por Tamanho: Inicialmente, as empresas são classificadas com base em seu tamanho de mercado. Normalmente, o tamanho de mercado é medido pela capitalização de mercado, que é o preço da ação multiplicado pelo número de ações em circulação. As empresas são divididas em duas categorias: pequenas empresas e grandes empresas, definidas respectivamente no 10°e 90° percentil. Além disso, os pontos de corte da relação B/M para uma região são os percentis 30º e 70º.

Construção de Portfólios: Em seguida, portfólios são criados para representar essas categorias de empresas. Um portfólio é composto por ações de várias empresas pertencentes à mesma categoria. Obtém-se 2 x 3 classificações, em termos de tamanho e relação B/M, produzindo seis carteiras ponderados pelo valor.

Cálculo de Diferença de Retornos: A diferença entre o retorno do portfólio de empresas pequenas e o retorno do portfólio de empresas grandes é calculada para cada período de tempo. Essa diferença de retornos é o que constitui o fator SMB.

Temos então que SMB é a média ponderada dos retornos considerando o valor de três carteiras de ações "pequenas" menos a média dos retornos das três carteiras de ações "grandes".

$SMB = 1/3 (\text{Pequeno Valor} + \text{Pequeno Neutro} + \text{Pequeno Crescimento}) - 1/3 (\text{Grande Valor} + \text{Grande Neutro} + \text{Grande Crescimento})$

HML (High minus Low)

Classificação por Valor Contábil (B/M): As empresas são classificadas com base em seu valor contábil em relação ao valor de mercado, medido pela relação "Book-to-Market" (B/M). O valor contábil representa o valor dos ativos da empresa registrados em seus livros contábeis, enquanto o valor de mercado é o preço atual das ações da empresa multiplicado pelo número de ações em circulação.

Construção de Portfólios**: Dois portfólios são criados com base na classificação B/M das empresas:

Portfólio de Alto B/M (High B/M): Este portfólio é composto por ações de empresas com valores contábeis significativamente mais altos em relação ao valor de mercado. Essas empresas são frequentemente consideradas "value stocks" (ações de valor).

Portfólio de Baixo B/M (Low B/M): Este portfólio é composto por ações de empresas com valores contábeis significativamente mais baixos em relação ao valor de mercado. Essas empresas são frequentemente consideradas "growth stocks" (ações de crescimento).

Cálculo da Diferença de Retornos: A diferença entre o retorno do portfólio de alto B/M e o retorno do portfólio de baixo B/M é calculada para cada período de tempo. Essa diferença de retornos é o que constitui o fator HML.

$SMB = 1/2 (\text{Pequeno Valor} + \text{Grande Valor}) - 1/2 (\text{Pequeno Crescimento} + \text{Grande Crescimento})$

Equação de Modelo de Fama-French

A representação do modelo de 3 fatores de Fama-French assume a seguinte forma:

$r_{it} - r_{ft} = \alpha_i + \beta_1 (r_{mt} - r_{ft}) + \beta_2 SMB_t + \beta_3 HML_t + \varepsilon_{it}$

Em que:

- $\alpha_i$ é o retorno excedente específico da ação $i$ , representando a parte do retorno que não pode ser explicada pelos fatores do modelo.

- $\beta_1$ , $\beta_2$ e $\beta_3$ são os coeficientes que relacionam o retorno da ação com os retornos do mercado, SMB e HML, respectivamente.

- $\varepsilon_{it}$ é o erro associado ao retorno da ação $i$ no período $t$ .

Lembrando que:

- $r_{it}$ representa o retorno de uma ação individual no período $t$ .

- $r_{ft}$ representa a taxa livre de risco.

- $r_{mt}$ denota o retorno de um índice do mercado de ações no período $t$ .

- $SMB_t$ (Small Minus Big) capta a diferença entre os retornos de carteiras diversificadas de ações de empresas pequenas e grandes, onde o tamanho é definido com base na capitalização de mercado das ações.

- Um coeficiente positivo para SMB indica que a estratégia de investir em ações de pequenas empresas em detrimento de ações de grandes empresas tende a produzir retornos superiores em relação ao mercado de ações em média.

- Um coeficiente negativo para SMB sugere que, em média, as ações de grandes empresas superam as ações de pequenas empresas.

- $HML_t$ (High Minus Low) capta a diferença entre os retornos de carteiras diversificadas de ações de alto e baixo valor contábil em relação ao valor de mercado (B/M).

- Um coeficiente positivo para HML indica que a estratégia de investir em ações de alto valor contábil em relação ao valor de mercado (ações de valor) em detrimento de ações de baixo valor contábil em relação ao valor de mercado (ações de crescimento) tende a produzir retornos superiores em relação ao mercado de ações em média.

- Um coeficiente negativo para HML sugere que, em média, as ações de crescimento superam as ações de valor.

A inclusão desses fatores por Fama e French tem o propósito de melhor capturar a variação sistemática nos retornos médios de carteiras típicas, em contraste com o uso exclusivo de um índice do mercado de ações. Esses fatores são respaldados por evidências empíricas e se alinham com a classificação de ações em termos de crescimento e valor.

Exemplo: Construindo um modelo de 3 fatores para o Mercado Brasileiro usando o Python

Vamo validar a regressão proposta por Fama-French para validar os efeitos de mercado, SMB e HML sobre o mercado acionário brasileiro. Como insumo de dados, utilizaremos:

Retorno do ativos: retorno simples diários, de ações obtidas através do Yahoo Finance. As ações escolhidas são aquelas destacadas na Composição do Índice Bovespa do dia 30/10/2023. Ao todo, foi obtido 86 ações, com destaque para o setor econômico pertencente de cada empresa.

Para a Taxa Livre de Risco, Retorno de Mercado, SMB e HML coletamos os dados dos fatores de risco disponibilizados pelo NEFIN.

O período de análise refere-se de janeiro de 2021 até agosto de 2023.

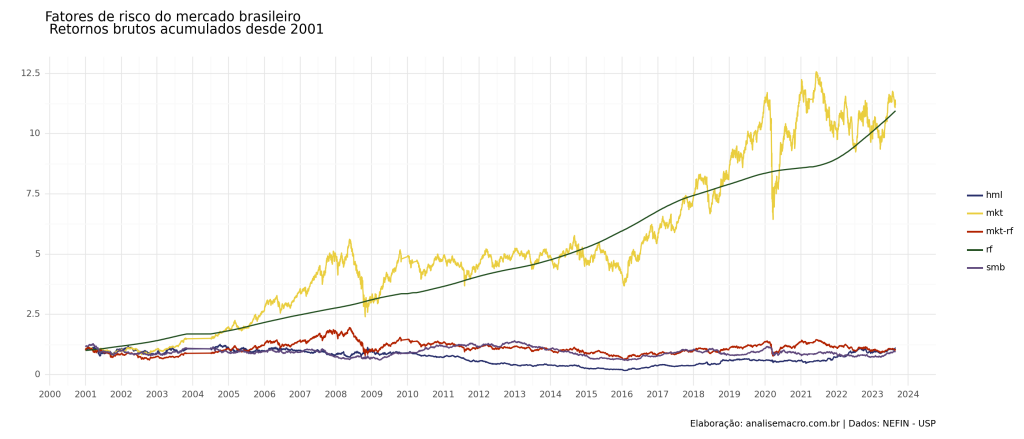
Alunos inscritos no curso de Mercado Financeiro e Gestão de Portfólio com o Python têm a oportunidade de adquirir conhecimento em todas as etapas a seguir, além de obter uma compreensão teórica abrangente das principais ferramentas utilizadas no Mercado Financeiro.

Fatores de Riscos

Abaixo, temos os valores do retornos acumulados dos fatores de risco construídos pelo NEFIN.

Regressão

Para avaliar os efeitos dos fatores, realizamos uma regressão linear múltipla por meio do método de Mínimos Quadrados Ordinários (OLS), tendo como variável dependente os retornos diários da VALE3. Abaixo, apresentamos a tabela com os principais resultados estatísticos:

Código

                            OLS Regression Results                            
==============================================================================
Dep. Variable:               vale3_sa   R-squared:                       0.394
Model:                            OLS   Adj. R-squared:                  0.389
Method:                 Least Squares   F-statistic:                     94.55
Date:                Tue, 31 Oct 2023   Prob (F-statistic):           3.59e-47
Time:                        13:28:03   Log-Likelihood:                 816.01
No. Observations:                 441   AIC:                            -1624.
Df Residuals:                     437   BIC:                            -1608.
Df Model:                           3                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
Intercept     -0.0006      0.002     -0.326      0.745      -0.004       0.003
mkt_rf         2.0455      0.162     12.654      0.000       1.728       2.363
smb            1.1491      0.156      7.343      0.000       0.841       1.457
hml           -0.4314      0.156     -2.765      0.006      -0.738      -0.125
==============================================================================
Omnibus:                       35.125   Durbin-Watson:                   2.007
Prob(Omnibus):                  0.000   Jarque-Bera (JB):              152.899
Skew:                          -0.059   Prob(JB):                     6.29e-34
Kurtosis:                       5.882   Cond. No.                         106.
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Qual leitura temos dos coeficientes em relação à ação da VALE3?

Coeficiente de mk_rf para VALE3:

O coeficiente de mk_rf para VALE3 indica como as ações da Vale S.A. (VALE3) reagem em relação ao mercado de ações em geral. Se o coeficiente de mk_rf for positivo, isso sugere que VALE3 tende a se mover na mesma direção que o mercado de ações global em resposta às mudanças no risco de mercado.
Um coeficiente positivo maior do que 1 indicaria que VALE3 é mais volátil do que o mercado, amplificando os movimentos do mercado.
Se o coeficiente de mk_rf para VALE3 for negativo, isso sugere que VALE3 tende a se mover na direção oposta ao mercado de ações global em resposta às mudanças no risco de mercado. Um coeficiente negativo maior do que -1 indicaria que VALE3 é mais volátil do que o mercado, mas em direção oposta.

Coeficiente de smb para VALE3:

O coeficiente de SMB para VALE3 (Small Minus Big) indica como o desempenho das ações da Vale em relação a ações de pequenas empresas se compara ao mercado.
Um coeficiente positivo sugere que VALE3 supera o mercado em relação a ações de pequenas empresas, ajustado pelo risco de mercado.
Um coeficiente negativo sugere que VALE3 tem um desempenho inferior em relação a ações de pequenas empresas, ajustado pelo risco de mercado.

Coeficiente de hml para VALE3:

O coeficiente de HML para VALE3 (High Minus Low) indica como o desempenho das ações da Vale em relação a ações de valor se compara ao mercado.
Um coeficiente positivo sugere que VALE3 supera o mercado em relação a ações de valor, ajustado pelo risco de mercado.
Um coeficiente negativo sugere que VALE3 tem um desempenho inferior em relação a ações de valor, ajustado pelo risco de mercado.

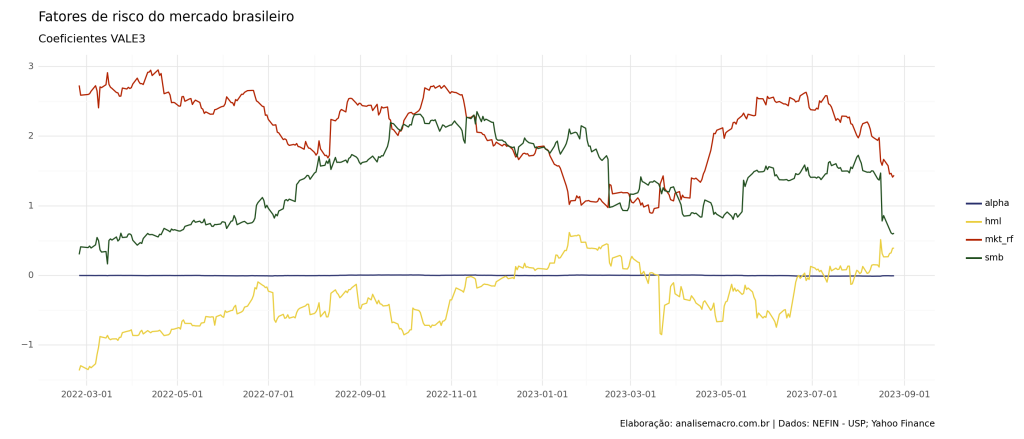
Regressão Móvel

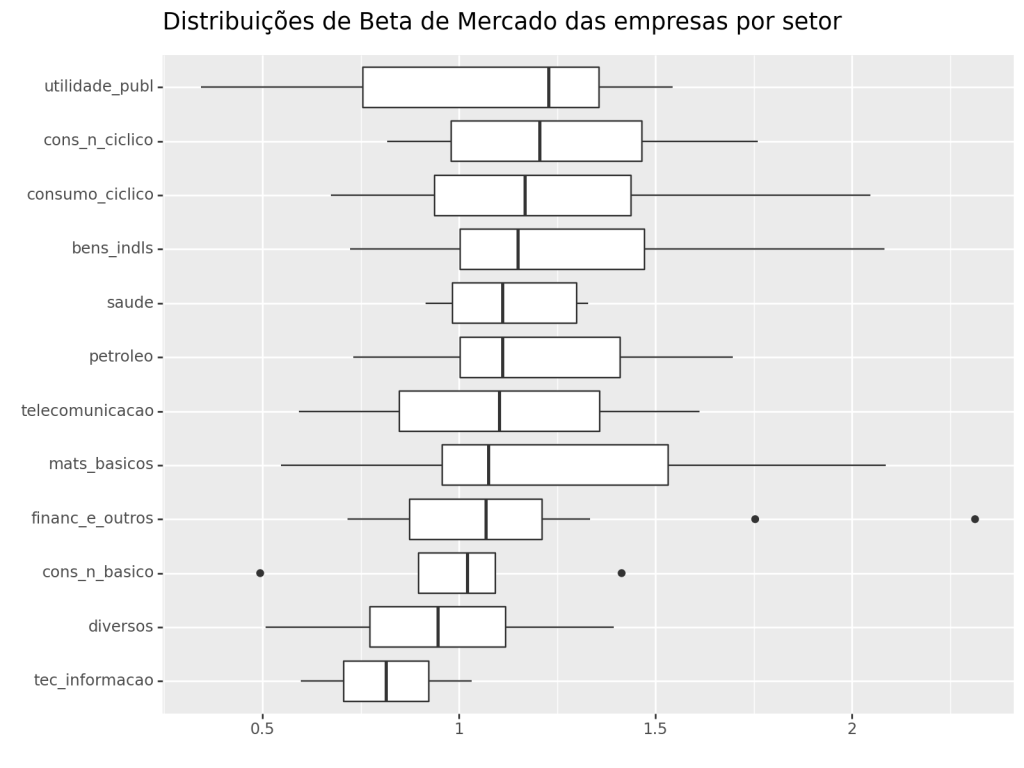
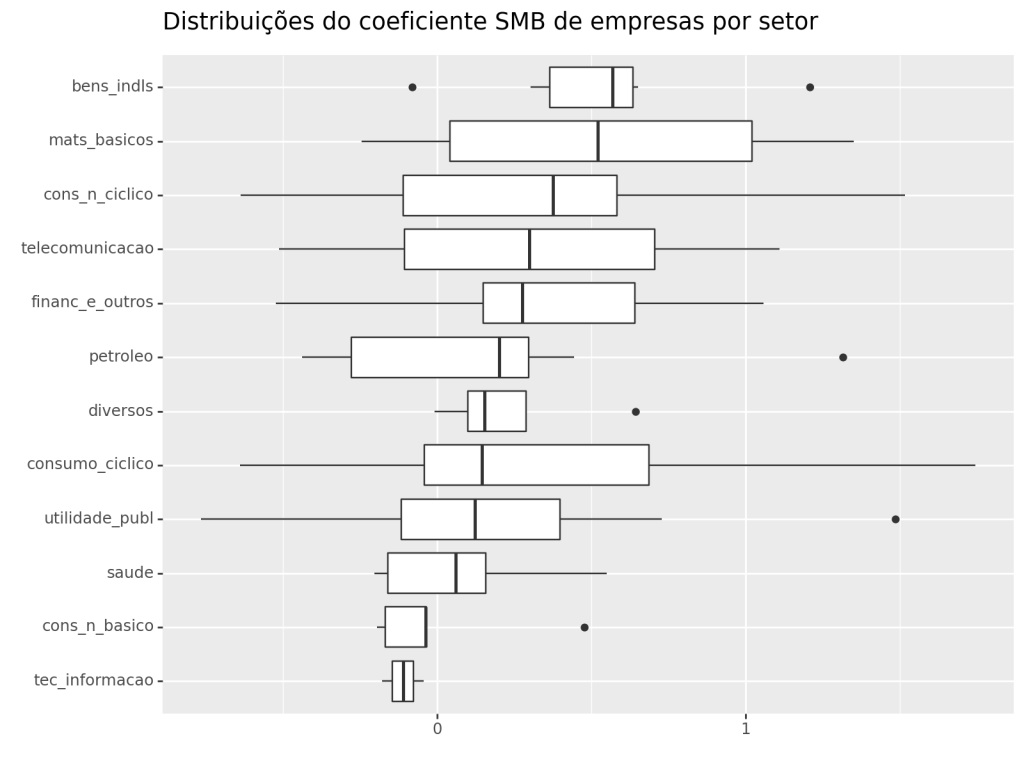
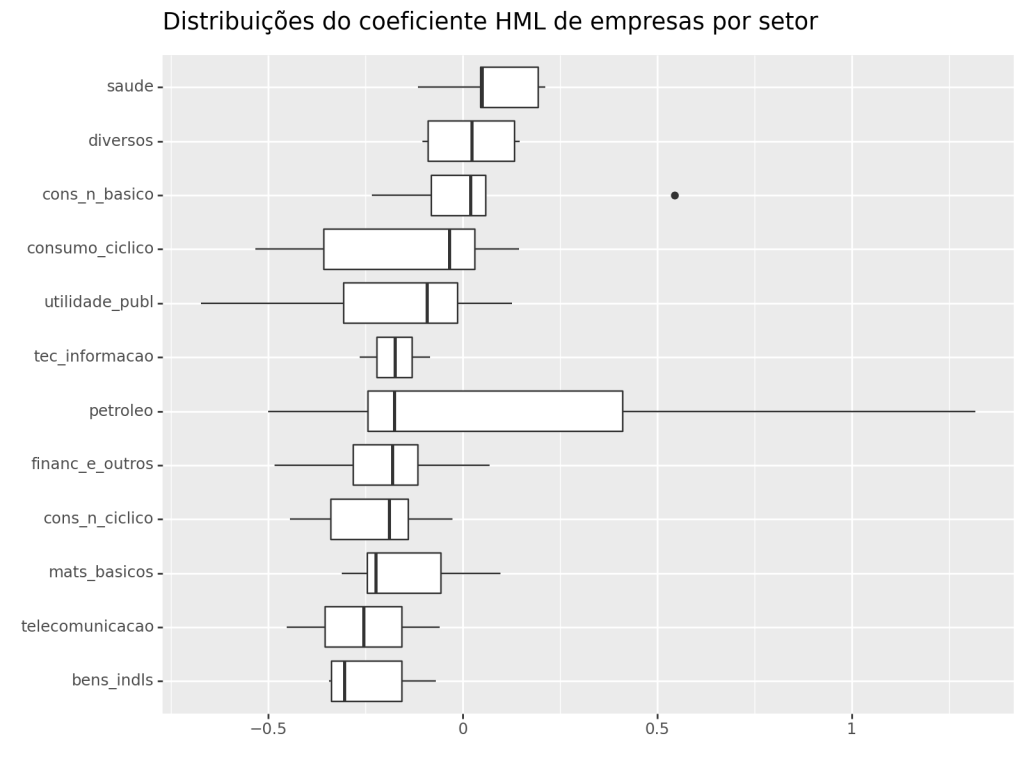
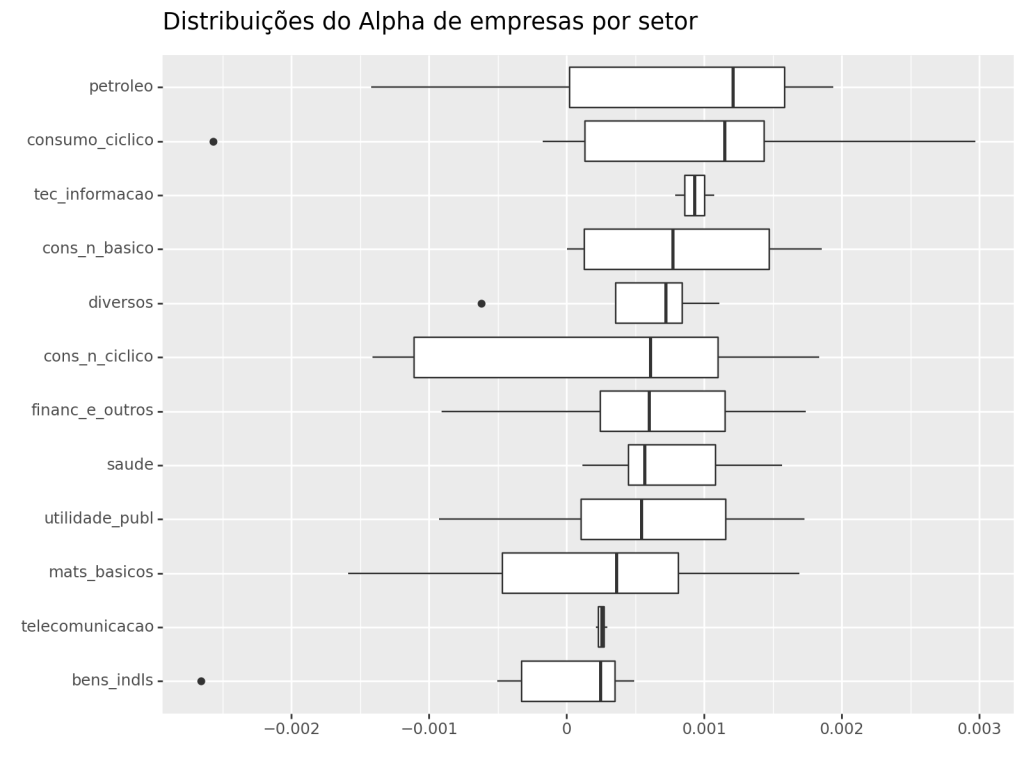
Uma abordagem útil para avaliar os coeficientes de cada fator é analisá-los ao longo do tempo por meio de uma regressão móvel. Utilizamos um período de janela fixa de 66 dias úteis como nossa amostra para essa análise.

Regressão Agrupado por Setor

Através da composição do Índice Bovespa, é possível determinar o setor ao qual cada empresa pertence. Uma abordagem para estimar os coeficientes de cada empresa ao longo do tempo é utilizar uma técnica de Regressão Móvel. Posteriormente, calcula-se a média dos coeficientes de todas as empresas dentro de cada setor durante o período. Essa metodologia possibilita realizar uma análise exploratória dos coeficientes estimados.

Quer aprender mais?

Clique aqui para fazer seu cadastro no Boletim AM e baixar o código que produziu este exercício, além de receber novos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas diretamente em seu e-mail.

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais
e conteúdos exclusivos sobre Análise de Dados!

Assinar

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Análise exploratória para modelagem preditiva no Python

Como usar modelos do Sklearn para previsão? Uma introdução ao Skforecast

Métodos de Reamostragem de Séries Temporais no Python

Coletando dados regionais do CAGED no Python

Coletando dados de Setores Censitários do Censo 2022 no Python

Estimando a inércia inflacionária através de modelos de espaço-estado usando Python

Outros artigos relacionados

Análise exploratória para modelagem preditiva no Python

Antes de desenvolver bons modelos preditivos é necessário organizar e conhecer muito bem os dados. Neste artigo, damos algumas dicas de recursos, como gráficos, análises e estatísticas, que podem ser usados para melhorar o entendimento sobre os dados usando Python.

Como usar modelos do Sklearn para previsão? Uma introdução ao Skforecast

Prever séries temporais é uma tarefa frequente em diversas áreas, porém exige conhecimento e ferramentas específicas. Os modelos de machine learning do Sklearn são populadores, porém são difíceis de aplicar em estruturas temporais de dados. Neste sentido, introduzimos a biblioteca Skforecast, que integra os modelos do Sklearn e a previsão de séries temporais de forma simples.

Métodos de Reamostragem de Séries Temporais no Python

Nesta postagem, vamos mostrar alguns métodos simples para lidar com a reamostragem de dados de séries temporais no Python.

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!