A combinação de diferentes ativos financeiros pode trazer benefícios, entre eles, conseguir uma boa diversificação de forma diluir os diversos riscos existentes. Porém, para construir portfólio, é necessário ter o entendimento correto sobre como construir formas de avaliação: de retorno e risco. No post de hoje, mostramos como podemos construir estas duas métricas utilizando o Python.
Um portfólio de ações consiste no conjunto de diferentes ativos escolhidos, através de uma metodologia, e mantidas durante um período de tempo. Ao realizar a escolha de ativos, é necessário que haja formas de avaliar o quão bem essas escolhas combinadas performaram, e qual o risco empregado por estes ativos.
Retornos do portfolio
Uma ação possui uma variação entre dois períodos históricos diferentes, podemos computar essa variação da seguinte forma:
Portanto, podemos saber o quanto essa ação rendeu de um período para outro. Mas, e para o caso de haver mais de uma ação em nossa carteira? Como podemos calcular? Para isso, devemos levar em consideração o peso de cada ação no total investido na carteira, obtendo a seguinte equação:
Em que 
é o peso do ativo no portfólio, podendo ser calculado como:
Ou seja, ponderamos o retorno do ativos com o seus pesos dentro da carteira.
Iremos realizar um exemplo utilizando ações da Ibovespa. Abaixo, capturamos o preço ajustado de quatro ações e computamos os retornos individuais.
Utilizamos o método pct_change para computar a variação diária dos preços ajustados das quatro ações.
Calculado os retornos, devemos obter os pesos de cada ativo. Selecionamos manualmente pesos iguais para todas as ações, construindo um portfolio conhecido como Equal Weighted Portfolio. Por fim, calculamos o retorno diário do portfólio multiplicando os pesos com os retornos e somando cada resultado.
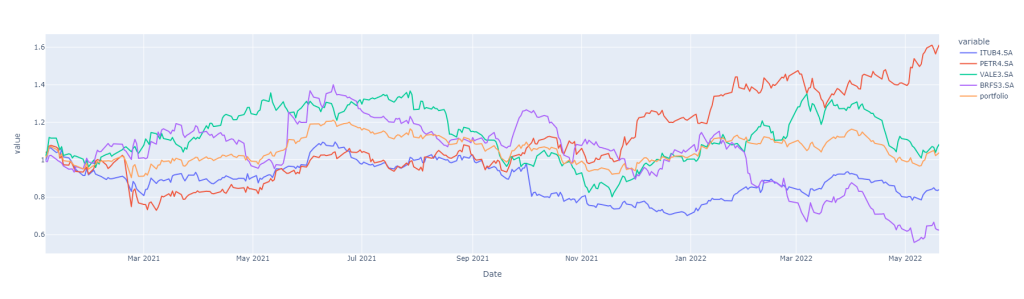
Retornos acumulados
Essa forma de cálculo representará os retornos diários dos ativos e do portfolio, o que não muito útil para acompanhar o acumulado ao longo de um período de tempo. Desta forma, podemos calcular o retorno acumulado das ações e do portfolio somando 1 aos retorno e utilizando a função cumprod() para calcular o produto acumulado das variações.
Retornos Anualizados
O retorno anualizado é uma forma de transformar a escala dos retornos em termos "anualizados" (o que é diferente de retornos no ano). O objetivo de computar este tipo de retorno se encontra no fato de poder comparar ativos de períodos e janelas de tempo diferentes em uma mesma escala.
A taxa anualizada para períodos diários é calculada como:
Em que 252 representa o número de dias úteis em um ano, e N o número de dias da série. Portanto, 
será a variação da última observação da série em relação a primeira observação, o mesmo que o retorno acumulado durante o período.
Abaixo, utilizaremos a última observação do retorno acumulado já computado.
Risco
Até agora já obtivemos as métricas necessárias para computar o retorno das ações, porém, devemos levar em conta o quão arriscado cada ativo é (para justificar o retorno e a alocação dos mesmos), bem como a composição do risco total do portfólio.
O risco (volatilidade) das ações individuais pode ser calculado como o desvio padrão de seus retornos. Calculamos abaixo com base em seu valor anualizado (que possui o mesmo significado que os retornos anualizados).
Entretanto, não podemos realizar o mesmo procedimento para o cálculo da volatilidade de um portfólio, afinal, as ações podem possuir uma relação, portanto, devemos levar em conta a correlação entre os ativos.
Calculamos a variância do portfólio em notação matricial
![$$\sigma^2_{pf} = \begin{bmatrix}{w_1 w_2}\end{bmatrix} \begin{bmatrix}{\sigma^2_1}&{\sigma_{1,2}} \\[0.3em] {\sigma_{2,1}}&{\sigma^2}\end{bmatrix} \begin{bmatrix}{w_1} \\{w_2}\end{bmatrix} $$](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-2012a2d8e9be4e4552e24491c2fdb065_l3.png "Rendered by QuickLaTeX.com")
E podemos facilmente realizar este cálculo utilizando o Python.
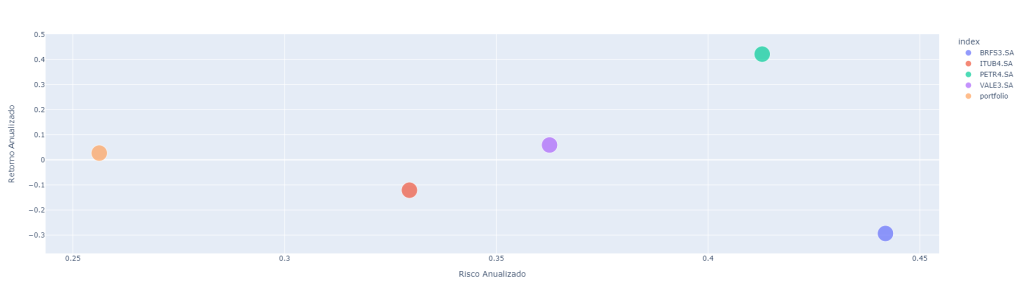
Juntamos os resultados dos retornos anualizados e do desvio padrão (risco) anualizado em um data frame, e geramos um gráfico mostrando o retorno das ações e do portfolio dado o nível de risco.
Quer saber mais?
Veja nosso curso de Python para Investimentos.
