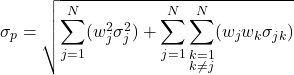A variância de um portfólio de investimento mensura a volatilidade de uma cesta de ativos financeiros. É interessante conhecer a contribuição de cada ativo para a volatilidade total da carteira. No post de hoje, mostramos como construir essas métricas e a construir um dashboard usando o Python.
Portfólio de investimentos
Um portfólio de investimentos é constituído por um conjunto de dois ou mais ativos, cada qual possuindo um peso ou porcentagem em relação ao total do portfólio, escolhidos de forma discricionária ou com base em fundamentos financeiros ou estatísticos.
O portfólio e os ativos financeiros que o compõem são mensurados em termos de retornos financeiros, definidos de acordo com a seguinte equação:
Para os ativos individuais:
E para o portfólio:
Vemos que o retorno histórico do portfólio é dado com base nos retornos dos ativos ponderados pela suas proporções em relação ao total do portfólio (peso).
Volatilidade do portfólio
Como dito, a volatilidade é definida de acordo com a variância ou desvio padrão do portfólio, entretanto, ao invés da fórmula usual que conhecemos do desvio padrão dos retornos históricos do ativo (vamos definir volatilidade apenas como o desvio padrão), dado por:
Ela não representaria de fato a variância do portfólio. Isso ocorre devido ao fato de que temos que levar em consideração que temos um conjunto de diferentes ativos na carteira, e isso leva a crer que esses ativos podem representar uma relação linear positiva ou negativa entre eles, o que pode de fato reduzir a volatilidade da carteira. Para representar essa questão, portanto, deve-se adicionar a formula a correlação/covariância entre os ativos que compõem a carteira, bem como os seus pesos relativos no portfólio para representar a variância (volatilidade) do portfólio. Portanto, utiliza-se a seguinte equação
Contribuição para a volatilidade
A contribuição para a volatilidade fornece uma decomposição ponderada da contribuição de cada elemento do portfólio para o desvio padrão de todo o portfólio.
Em termos formais, é definida pelo nome de contribuição marginal, que é basicamente a derivada parcial do desvio padrão do portfólio em relação aos pesos dos ativos. A interpretação da fórmula da contribuição marginal, entretanto, não é tão intuitiva, portanto, é necessário obter medidas que possibilitem analisar os componentes. Veremos portanto como calcular os componentes da contribuição e a porcentagem da contribuição.
1 - Contribuição Marginal
A contribuição marginal é calculada conforme:
2 - Componentes da Contribuição
Os Componentes da Contribuição é calculada conforme:
3 - Porcentagem da Contribuição
A Porcentagem da Contribuição é calculada conforme:
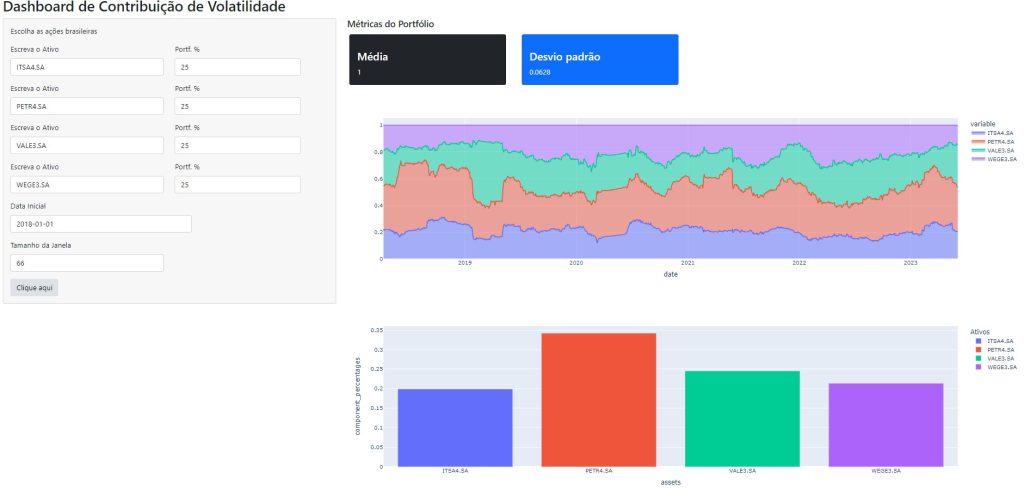
Dashboard de Contribuição de Volatilidade no Python
Para obter todo o código do processo de criação do Dashboard, faça parte do Clube AM, o repositório de códigos da Análise Macro, contendo exercícios semanais.
Para facilitar todo o trabalho de verificar a contribuição da volatilidade, é possível criar um Dashboard, que automatiza todo o processo de coleta, tratamento, e a visualização de dados. No Dashboard abaixo, o processo de coleta de dados financeiros foi feito por meio da biblioteca yfinance. O Dashboard é construído no ambiente da biblioteca Shiny e os gráficos construídos por meio do Plotly.
_____________________
Quer saber mais?
Veja nossa trilha de cursos de Finanças Quantitativas