No post de hoje investigamos a volatilidade do câmbio utilizando um Garch(1,1).
Uma importante medida em finanças é o risco associado a um ativo e a volatilidade de ativos é talvez a medida de risco mais utilizada. Ainda que a volatilidade seja bem definida, ela não é diretamente observada na prática. Nós observamos os preços dos ativos e seus derivativos. A volatilidade deve ser, então, estimada com base nesses preços observados.
Existem uma série de formas de estimar a volatilidade, desde a mais simples, usando o desvio padrão, até mais robustos tal como Garch.
O interessante de modelos do tipo Garch é que permitem modelar a volatilidade com base nos retornos ao quadrado passados da série e também da volatilidade passada, o que permite que efeitos práticos possam ser incluídos no modelo.
Para entender como foi criado o gráfico e o modelo abaixo, faça parte do Clube AM, o repositório de códigos da Análise Macro, contendo exercícios semanais de R e Python.
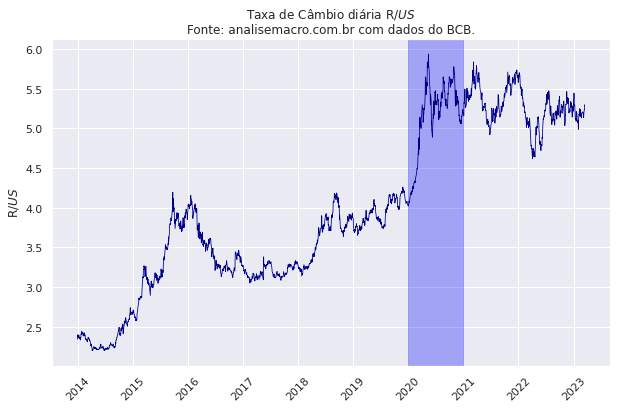
Vejamos abaixo a série da Taxa de Câmbio R$/U$ no gráfico abaixo.
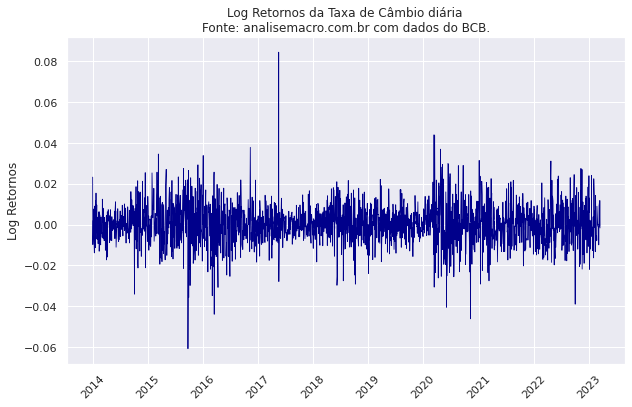
Podemos transformar a série do preço do câmbio em log retornos, o que permitirá modelarmos a série usando um Garch(1,1).
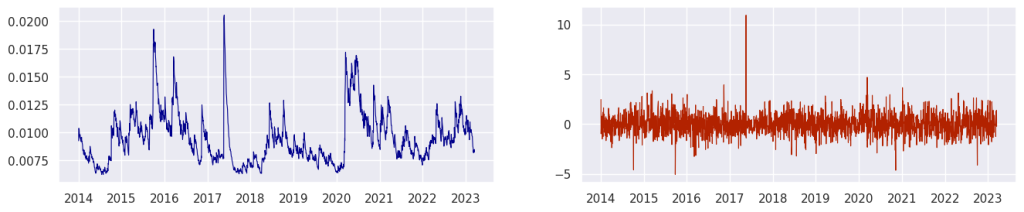
Abaixo temos o resultado do Garch(1,1) nos log retornos do câmbio. No primeiro gráfico, da esquerda, tem-se a volatilidade estimada, enquanto no segundo gráfico a direta tem-se os erros padronizados do modelo, permitindo avaliar o resultado.
Abaixo a tabela demonstrando os resultado modelo
_____________________________________
Quer aprender mais?
Seja um aluno da nossa trilha de Macroeconomia Aplicada e aprenda a criar projetos voltados para a Macroeconomia