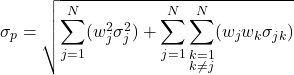Explicando a variância de um portfólio de investimentos

A variância de um portfólio de investimento mensura a volatilidade de uma cesta de ativos financeiros. É interessante conhecer a contribuição de cada ativo para a volatilidade total da carteira, portanto, no post de hoje iremos mostrar como construir um código em R para mensurar essa medida.

Portfólio de investimentos

Um portfólio de investimentos é constituído por um conjunto de dois ou mais ativos, cada qual possuindo um peso ou porcentagem em relação ao total do portfólio, escolhidos de forma discricionária ou com base em fundamentos financeiros ou estatísticos.

O portfólio e os ativos financeiros que o compõem são mensurados em termos de retornos financeiros, definidos de acordo com a seguinte equação:

Para os ativos individuais:

E para o portfólio:

Vemos que o retorno histórico do portfólio é dado com base nos retornos dos ativos ponderados pela suas proporções em relação ao total do portfólio (peso).

Vamos calcular o retorno histórico dos ativos do portfólio usando o R. Vamos definir quatro ações escolhidas de forma aleatória, durante o período de 01/2016 a 06/2022, coletando os dados através do Yahoo Finance, calculando os retornos individuais e em seguida construindo um portfolio Equal Weighted Portfolio (pesos iguais).

library(quantmod)
library(PerformanceAnalytics)
library(xts)
library(tidyverse)

</pre>
# Tickers das ações
symbols <- c("MGLU3.SA", "ABEV3.SA", "ITUB4.SA", "WEGE3.SA")

# Datas
start = "2016-01-01" # início
end = "2022-07-01" # fim

# Define o enviroment para salvar os objetos de preços
env <- new.env()

# Coleta os preços das ações
getSymbols(symbols, # tickers
src = 'yahoo', # fonte
from = start, # início
to = end, # fim
env = env, # env dos objetos
auto.assign = TRUE) # declara automaticamente

# Junta os dados dos preços
prices <- do.call(merge, lapply(env, Ad))

# Renomeia as colunas
colnames(prices) <- c(symbols)

# Transforma de diário para mensal
prices_monthly <- to.monthly(prices, indexAt = "first", OHLC = FALSE)

# Calcula os retornos
returns <-
na.omit(Return.calculate(prices_monthly, method = "discrete"))

# Define a alocação dos ativos (pesos EWP)
w = rep(1, length(symbols)) / length(symbols)

# Calcula os retornos do portfólio
return_port <- Return.portfolio(returns, weights = w)
<pre>

O retorno histórico possibilita o cálculo de diversos parâmetros, como no caso, da variância ou desvio padrão histórico do portfólio, representando uma medida de volatilidade.

Volatilidade do portfólio

Como dito, a volatilidade é definida de acordo com a variância ou desvio padrão do portfólio, entretanto, ao invés da fórmula usual que conhecemos do desvio padrão dos retornos históricos do ativo (vamos definir volatilidade apenas como o desvio padrão), dado por:

Ela não representaria de fato a variância do portfólio. Isso ocorre devido ao fato de que temos que levar em consideração que temos um conjunto de diferentes ativos na carteira, e isso leva a crer que esses ativos podem representar uma relação linear positiva ou negativa entre eles, o que pode de fato reduzir a volatilidade da carteira. Para representar essa questão, portanto, deve-se adicionar a formula a correlação/covariância entre os ativos que compõem a carteira, bem como os seus pesos relativos no portfólio para representar a variância (volatilidade) do portfólio. Portanto, utiliza-se a seguinte equação

# Calcula a volatilidade do portfólio (desvio-padrão) -------------

## Na mão
covariance_matrix <- cov(returns) # matriz de covariância

sd_portfolio <- sqrt(t(w) %*% covariance_matrix %*% w) # desvio padrão do portfólio

# Usando função pronta
port_sd <- StdDev(returns,
weights = w)

Desta forma, temos a medida de volatilidade da carteira, que pode trazer informações valiosas, entretanto, seria também interessante saber a contribuição de cada ativo para a volatilidade total do portfólio.

Contribuição para a volatilidade

A contribuição para a volatilidade fornece uma decomposição ponderada da contribuição de cada elemento do portfólio para o desvio padrão de todo o portfólio.

Em termos formais, é definida pelo nome de contribuição marginal, que é basicamente a derivada parcial do desvio padrão do portfólio em relação aos pesos dos ativos. A interpretação da fórmula da contribuição marginal, entretanto, não é tão intuitiva, portanto, é necessário obter medidas que possibilitem analisar os componentes. Veremos portanto como calcular os componentes da contribuição e a porcentagem da contribuição.

1 - Contribuição Marginal

A contribuição marginal é calculada conforme:

É possível calcular no R da seguinte forma:

# Contribuição da volatilidade -----------------------

## Cálculo a mão

# Contribuição Marginal de cada ativo
marginal_contribution <- w %*% covariance_matrix / sd_portfolio[1, 1]

2 - Componentes da Contribuição

Os Componentes da Contribuição é calculada conforme:

É possível calcular no R da seguinte forma:

# Contribuição dos componentes
component_contribution <- marginal_contribution * w 

# A soma deve ser igual ao total do portfólio
components_summed <- rowSums(component_contribution)

3 - Porcentagem da Contribuição

A Porcentagem da Contribuição é calculada conforme:

É possível calcular no R da seguinte forma:

# Contribuição percentual dos componentes
component_percentages <- component_contribution / sd_portfolio[1, 1]

É possível calcular diretamente por meio da função StdDev do pacote {PortfolioAnalytics}, usando o argumento portfolio_method = "component".

## Cálculo com a função pronta ---------------------------

port_cont <- StdDev(retunrs,
weights = w,
portfolio_method = "component")

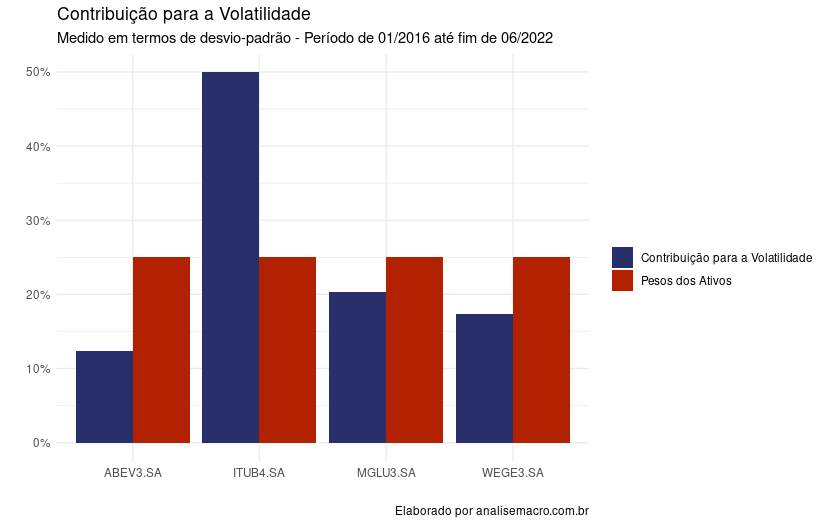
Visualizando os dados

O interessante dos resultados é a sua visualização para entender a dinâmica da contribuição do risco do portfólio. Portanto, iremos transformar os dados em tibble e em seguida, usaremos o {ggplot2} para visualizar os resultados.

## Visualização -------

# Transforma em tibble

cont_by_hand <-
tibble(symbols, w, as.vector(component_percentages)) %>%
rename(asset = symbols,
'Pesos dos Ativos' = w,
'Contribuição para a Volatilidade' = `as.vector(component_percentages)`)

# Visualiza

cont_by_hand %>%
pivot_longer(names_to = "type", values_to = "values", -asset) %>%
ggplot()+
aes(x = asset, y = values, fill = type)+
geom_col(position = "dodge")+
scale_y_continuous(labels = scales::percent)+
labs(title = "Contribuição para a Volatilidade",
subtitle = "Medido em termos de desvio-padrão - Período de 01/2016 até fim de 06/2022",
x = "",
y = "",
caption = "Elaborado por analisemacro.com.br")+
scale_fill_manual(values = c("#282f6b", "#b22200"),
name = "")+
theme_minimal(legend.position = "bottom")

______________________________________

Quer saber mais?

Veja nossa trilha de Finanças Quantitativas.