A regressão Fama-MacBeth é um método utilizado para estimar parâmetros em modelos de precificação de ativos, como o Modelo de Precificação de Ativos de Capital (CAPM). O método estima os betas e prêmios de risco para quaisquer fatores de risco que se espera que determinem os preços dos ativos. O método opera com vários ativos ao longo do tempo (dados em painel). Os parâmetros são estimados em duas etapas. Vamos aplicar a regressão Fama-Macbeth para dados do mercado acionário brasileiro utilizando o Python.
A regressão linear é um modelo estatístico que é frequentemente usado para analisar a relação entre duas variáveis. No factor investing, a regressão linear é utilizada para analisar a relação entre a rentabilidade de uma ação e os fatores selecionados. Por exemplo, uma regressão pode ser usada para avaliar a relação entre a rentabilidade de uma ação e seu valor relativo (um fator de estilo comum).
CAPM (Capital Asset Pricing Model)
O CAPM (Capital Asset Pricing Model) é um modelo financeiro utilizado para estimar o retorno esperado de um ativo financeiro. Ele foi desenvolvido com base na ideia de que o retorno de um ativo financeiro é composto por dois componentes: o retorno livre de risco e o prêmio de risco.
O retorno livre de risco é o retorno que um investidor pode obter sem correr risco algum, geralmente associado a investimentos em títulos públicos. O prêmio de risco, por sua vez, é a compensação que um investidor deve receber para correr o risco de investir em um ativo financeiro mais arriscado, como ações.
Com o retorno da carteira de mercado representando o risco sistemático, chega-se a conclusão de que as variações do portfólio de mercado representaria um fator importante na variação do retorno de uma ação. Para tanto, na formulação do CAPM foi levado em conta o quanto estes retornos se relacionam, representado pelo Beta de mercado, formando então a seguinte equação calculada através de uma Regressão Linear via MQO:
O CAPM (Capital Asset Pricing Model) é um modelo financeiro utilizado para estimar o retorno esperado de um ativo financeiro. Ele foi desenvolvido com base na ideia de que o retorno de um ativo financeiro é composto por dois componentes: o retorno livre de risco e o prêmio de risco.
O retorno livre de risco é o retorno que um investidor pode obter sem correr risco algum, geralmente associado a investimentos em títulos públicos. O prêmio de risco, por sua vez, é a compensação que um investidor deve receber para correr o risco de investir em um ativo financeiro mais arriscado, como ações.
Com o retorno da carteira de mercado representando o risco sistemático, chega-se a conclusão de que as variações do portfólio de mercado representaria um fator importante na variação do retorno de uma ação. Para tanto, na formulação do CAPM foi levado em conta o quanto estes retornos se relacionam, representado pelo Beta de mercado, formando então a seguinte equação calculada através de uma Regressão Linear via MQO:
em que representa o excesso de retorno de um ativo, dado pela subtração do retorno do ativo em relação ao retorno da taxa de juros livre de risco.
o excesso de retorno do portfolio de mercado, sendo representado pela diferença do retorno de mercado e do retorno da taxa de juros livre de risco.
é o coeficiente da regressão que demonstrará o efeito da variação do excesso de retorno do mercado no excesso de retorno do ativo.
é o erro da regressão.
O objetivo então é obter as taxas de retorno do ativo, do portfólio de mercado e da taxa de juros livre de risco e estimar o Beta de mercado (coeficiente de regressão) .
Modelo de 3 fatores de Fama e French
Como uma extensão do CAPM, o modelo de Fama French relaciona o excesso de retorno (diferença do retorno do ativo com o retorno livre de risco) em relação ao prêmio pelo risco do mercado, além também de dois outro fatores: HML (High minus Low), sendo a diferença entre os retornos das firmas que tenham um alto book-to-market e baixo book-to-market; e SMB (Small minus Big Factor), sendo a diferença entre empresas grandes e pequenas.
A sensitividade de cada fator é medido pelos da equação, sendo possível mensurar os riscos que uma carteira de ativos sofrem, bem como traçar estratégias com as informações da influência de cada fator de risco.
Regressão de Fama-Macbeth
A regressão de Fama-MacBeth é um método utilizado para estimar parâmetros de modelos de fatores de ativos. O método estima os betas e os prêmios de risco para quaisquer fatores de risco que se espera determinar os preços dos ativos. O método trabalha com vários ativos ao longo do tempo (dados em painel).
O procedimento de Fama-MacBeth é uma abordagem simples em duas etapas: A primeira etapa usa os fatores (características) como variáveis explicativas em regressões cross-section. Por exemplo, se R_{i,t} denota os retornos em excesso do ativo i no mês t+1, então o modelo de três fatores de Fama-French implica o seguinte processo de geração de retornos.
Aqui, estamos interessados na compensação de pela exposição a cada fator de risco
em cada ponto no tempo, ou seja, o prêmio de risco. Observe a terminologia:
é uma característica específica do ativo, como uma exposição a fator ou uma variável contábil. Se houver uma relação linear entre os retornos esperados e a característica em um determinado mês, esperamos que o coeficiente de regressão reflita essa relação, ou seja,
representa a compensação pelo risco.
No segundo passo, a média da série temporal das estimativas
pode então ser interpretada como o prêmio de risco para o fator de risco específico
. Consideramos a regressão cross-section padrão para prever retornos futuros. Se as características forem substituídas por variáveis no tempo
, então a abordagem de regressão captura atributos de risco em vez de prêmios de risco.
Antes de passarmos para a implementação, é importante destacar que as características, por exemplo, , são frequentemente estimadas em uma etapa separada antes de aplicar a metodologia Fama-MacBeth propriamente dita. Você pode pensar nisso como uma etapa 0. Portanto, pode surgir a preocupação de que os erros de
impactem os erros padrão dos prêmios de risco. O erro de medição em
de fato afeta as estimativas dos prêmios de risco, ou seja, leva a estimativas enviesadas. A literatura fornece ajustes para esse viés mas também mostra que o viés tende a zero conforme
.
Os alunos do curso de Mercado Financeiro e Gestão de Portfólio usando o Python, têm a oportunidade de adquirir um conhecimento abrangente em todas as fases do processo, desde a coleta e a preparação dos dados até a análise, o desenvolvimento de modelos econométricos e a comunicação dos resultados, tudo isso utilizando Python como ferramenta principal.
Fonte de dados
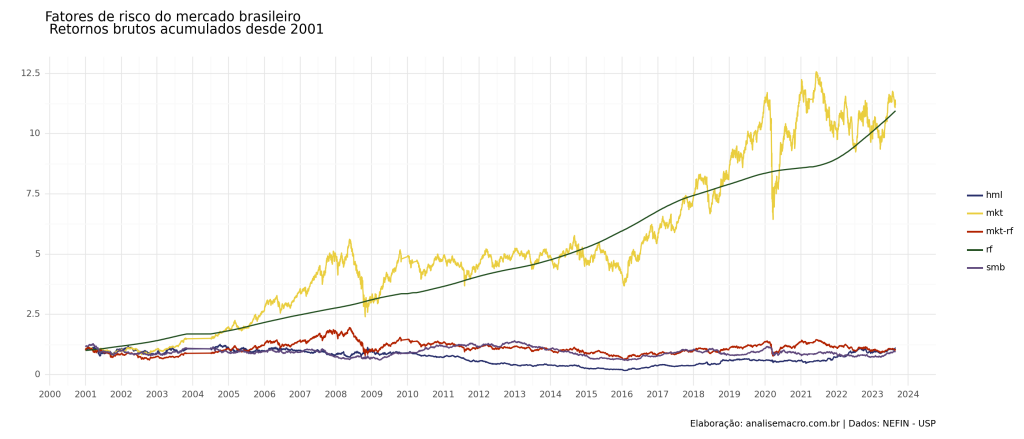
Para a fonte de dados, utilizamos o site do Centro Brasileiro de Pesquisa em Economia Financeira da Universidade de São Paulo, que disponibiliza diversos dados de fatores de risco. Dentre os disponíveis, encontramos os seguintes fatores:
- Fator de Mercado (risco de mercado);
- SMB (Small minus Big);
- HML (High minus Low);
- MOM (Winner Minus Losers);
- IML (Illiquid Minus Liquid);
- Risk Free (Taxa de juros livre de risco).
Para dados de ações, capturamos os preços de fechamento ajustado, conforme a lista produzida pela composição do Ibovespa. Transformamo-os em retorno simples.
Etapa 0: estimação dos coeficientes
Realizamos a estimação dos coeficientes dos fatores em janelas móveis.
Código
| Date | alpha | mkt_rf | smb | hml | mom | illiq | tickers | |
|---|---|---|---|---|---|---|---|---|
| 0 | 2022-02-24 | 0.004699 | 0.707604 | -0.124172 | -0.622303 | 0.065558 | -0.230525 | abev3_sa |
| 1 | 2022-02-25 | 0.004245 | 0.582529 | -0.019896 | -0.664530 | 0.020575 | -0.158783 | abev3_sa |
| 2 | 2022-03-02 | 0.004499 | 0.617487 | -0.042447 | -0.667605 | 0.028862 | -0.175582 | abev3_sa |
| 3 | 2022-03-03 | 0.003994 | 0.610233 | -0.045286 | -0.671579 | 0.053363 | -0.174621 | abev3_sa |
| 4 | 2022-03-04 | 0.004338 | 0.537250 | -0.033643 | -0.676013 | 0.070640 | -0.152772 | abev3_sa |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 32331 | 2023-08-21 | -0.000854 | 0.996233 | 0.060813 | -0.426584 | -0.679345 | -0.780151 | yduq3_sa |
| 32332 | 2023-08-22 | -0.000952 | 0.998265 | 0.045137 | -0.412463 | -0.663556 | -0.727358 | yduq3_sa |
| 32333 | 2023-08-23 | -0.000461 | 1.054750 | 0.063340 | -0.280982 | -0.650059 | -0.730254 | yduq3_sa |
| 32334 | 2023-08-24 | -0.000359 | 0.997268 | 0.000426 | -0.296343 | -0.745405 | -0.633455 | yduq3_sa |
| 32335 | 2023-08-25 | -0.000538 | 1.006111 | -0.004915 | -0.305571 | -0.776918 | -0.640667 | yduq3_sa |
32336 rows × 8 columns
Importante a necessidade de criar uma defasagem dos fatores, de forma que o modelo não esteja sujeito a vazamento de informações.
Regressão Cross-section
Em seguida, realizamos as regressões em cross-section com as características como variáveis explicativas para cada mês. Regredimos os retornos dos ativos de teste em um ponto específico no tempo nas características de cada ativo. Ao fazer isso, obtemos uma estimativa dos prêmios de risco para cada ponto no tempo.
Código
| Date | Intercept | mkt_rf | smb | hml | mom | illiq | |
|---|---|---|---|---|---|---|---|
| 0 | 2022-02-24 | 0.000086 | -0.004153 | 0.001749 | -0.042807 | -0.005922 | -0.012396 |
| 1 | 2022-02-25 | -0.007713 | 0.014703 | -0.032058 | 0.006359 | -0.002233 | -0.021541 |
| 2 | 2022-03-02 | -0.014783 | 0.031044 | -0.034114 | -0.016873 | 0.001255 | -0.032883 |
| 3 | 2022-03-03 | -0.002294 | 0.005283 | -0.007758 | -0.000667 | 0.002041 | -0.019288 |
| 4 | 2022-03-04 | -0.004149 | -0.006206 | -0.027628 | -0.013968 | -0.005534 | -0.024622 |
| ... | ... | ... | ... | ... | ... | ... | ... |
| 371 | 2023-08-21 | -0.015510 | 0.006108 | -0.004718 | -0.002414 | 0.011008 | 0.006818 |
| 372 | 2023-08-22 | 0.005794 | 0.008193 | 0.012423 | 0.005031 | 0.020588 | 0.001992 |
| 373 | 2023-08-23 | -0.043809 | 0.059965 | -0.025611 | 0.094171 | -0.028069 | -0.009228 |
| 374 | 2023-08-24 | 0.010821 | -0.018746 | -0.002693 | 0.008237 | -0.009432 | 0.000834 |
| 375 | 2023-08-25 | 0.007286 | -0.014979 | -0.017014 | 0.005941 | 0.004483 | -0.005264 |
376 rows × 7 columns
Agregação das Séries Temporais
Agora que temos as estimativas dos prêmios de risco para cada período, podemos fazer uma média ao longo da dimensão da série temporal para obter o prêmio de risco esperado para cada característica. Da mesma forma, criamos manualmente as estatísticas de teste t-test para cada regressor, as quais podemos então comparar com os valores críticos usuais de 1.96 ou 2.576 para testes de significância bilateral.
Usualmente, realizamos o ajuste para problemas de autocorrelação conforme os Erros Padrão de Newey and West.
Código
| factor | risk_premium | t_statistic | t_statistic_newey_west | |
|---|---|---|---|---|
| 0 | Intercept | -0.010 | -0.201 | -0.218 |
| 1 | hml | 0.090 | 1.164 | 1.051 |
| 2 | illiq | -0.064 | -1.085 | -1.065 |
| 3 | mkt_rf | -0.015 | -0.198 | -0.197 |
| 4 | mom | 0.102 | 1.112 | 1.034 |
| 5 | smb | 0.014 | 0.192 | 0.188 |
_____________________________________
Quer aprender mais?
Clique aqui para fazer seu cadastro no Boletim AM e baixar o código que produziu este exercício, além de receber novos exercícios com exemplos reais de análise de dados envolvendo as áreas de Data Science, Econometria, Machine Learning, Macroeconomia Aplicada, Finanças Quantitativas e Políticas Públicas diretamente em seu e-mail.