O Filtro de Kalman é onipresente em problemas de controle de engenharia, incluindo orientação e navegação, análise de trajetória de naves espaciais e fabricação, entretanto, também é amplamente utilizado em finanças quantitativas. Neste post de hoje, trataremos de introduzir o Filtro de Kalman de forma intuitiva aplicando um exemplo de estimação do Beta de Mercado utilizando o algoritmo no Python.
O filtro de Kalman é um algoritmo que usa observações com ruídos de um sistema ao longo do tempo para estimar os parâmetros do sistema (alguns dos quais não são observáveis) e prever observações futuras. A cada passo de tempo, ele faz uma previsão, recebe uma medição e se atualiza com base na comparação entre a previsão e a medição. Esse algoritmo faz parte de um sistema de espaço de estados.
A premissa geral de um modelo de espaço de estados é que temos um conjunto de estados que evoluem no tempo (como a razão de hedge entre dois pares cointegrados de ações), mas nossas observações desses estados contêm ruído estatístico (como ruído de microestrutura de mercado) , e, portanto, não podemos observar diretamente os estados "verdadeiros".
O objetivo do modelo de espaço de estados é inferir informações sobre os estados, dadas as observações, à medida que novas informações chegam. Ou seja, utiliza-se de um algoritmo recursivo que permite usar uma série temporal observável para estimar uma série não observável, chamada de variável de estado, sendo construído na forma de estado-espaço.
Na imagem, temos de forma ilustrada o processo do algoritmo de Kalman.
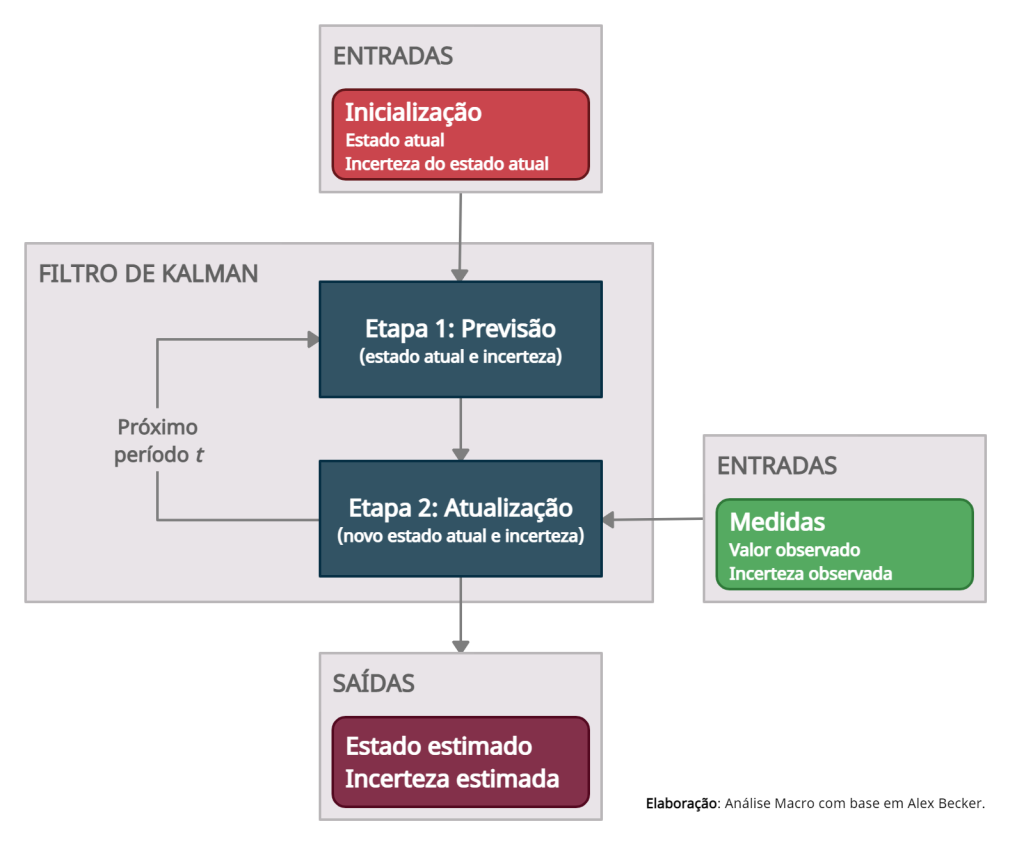
Usualmente, existem três tipos de inferência que nós estamos interessado quando considerado modelos de espaço estado:
- Previsão - Prevê os valores valores subsequentes do estado
- Filtragem - Estimação dos valores atuais do estado através das observações passadas e atuais do estado
- Suavização - Estimação dos valores passados do estado de acordo com as observações
Não iremos discutir os aspectos matemáticos do algoritmo, visto que é complexo e exige a demonstração de diversas equações. Seguiremos apenas na parte intuitiva, e que será suficiente para entender a estimação do Beta a partir do Filtro de Kalman.
O interessante do Filtro de Kalman é a sua possibilidade de ser utilizado para estimar valores através de uma regressão. Como o Filtro de Kalman é recursivo, ou seja, é baseado na repetição e atualização dos valores para estimar uma variação desconhecida, podemos utilizá-lo para estimar o Beta de Mercado móvel de uma ação, visto que o Beta varia ao longo do tempo.
Visto que o valores de Beta variam ao longo de tempo, é normal utilizar-se de regressões móveis, como forma de obter o valor do Beta de uma ação no período mais recente. Por definição, neste processo, o usuário deve escolher o período da janela do cálculo. Pelo Filtro de Kalman, isso não é necessário, visto que utiliza-se da última observação apenas para estimar o valores desconhecidos no estado atual, e o próprio algoritmo atualiza as mudanças estruturais dos dados ao longo do tempo. Isso é extremamente útil para alguns tipos de estratégias de trading que necessitam dos melhores valores mais recentes.
Agora, seguiremos para a demonstração com um código de construção do Beta através da biblioteca pykalman.
Utilizaremos o pandas_datareader para a importação dos preços e o pandas e numpy para cálculo dos retornos da ação e do retorno de mercado com a finalidade de calcular o beta pelo Filtro da Kalman.
No código abaixo tratamos de importar os dados da ITUB4 e calcular os seus retornos diários no período de 2019 a 07/2022. Realizamos o mesmo processo para o Ibovespa.
Por fim, devemos definir como iremos calcular o Filtro de Kalman utilizando a classe KalmanFilter, definindo os valores do parâmetros iniciais do algoritmo. Para entender mais sobre como são definidos os argumento da função, veja a documentação da biblioteca.
Por fim, procedemos com o cálculo dos valores, com o método filter(). O resultado será o estado dos valores do coeficiente da regressão e seu intercepto, bem com o estado das covariâncias.
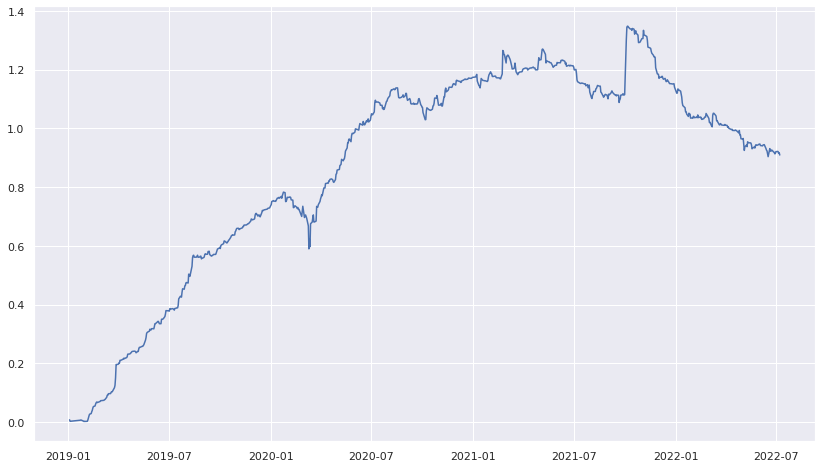
Abaixo, podemos visualizar o Beta estimado ao longo do tempo.
Interessante notar as mudanças ao longo do tempo do coeficiente, corroborando para a utilização em estratégias que necessitam de valores dinâmicos do Beta.
__________________________________________________
Quer saber mais?
Veja nosso curso de Python para Investimentos.