No post de hoje iremos mostrar como criar o modelo de precificação conhecido como Market Model. O propósito do modelo segue o mesmo caminho que outros modelos de fatores, em que é escolhido uma proxy de risco para explicar a variação do retorno de um ativo. Mostraremos também como criar uma regressão móvel para o modelo.
No caso do Market Model, pode ser considerado um dos modelos mais simples dentro da literatura e do mundo real de finanças, em que é necessário somente os dados de um índice de mercado que queira ser acompanhado, diferente de outros modelos, que se estendem na utilização de proxys para portfolios de mercado ou o efeito do tamanho das empresas sobre o ativo, podendo ou não serem modelos multi-fatores.
O Market Model não pressupõe a preocupação de se utilizar o verdadeiro portfolio de mercado, apenas um índice, portanto não é necessário que seja utilizado a taxa de juros livre de risco para realizar seu cálculo. Sua equação é definida como:
(1)
em que é o retorno do ativo,
é o retorno em excesso,
é o coeficiente que mede a sensibilidade do ativo em relação ao índice e
é o retorno do índice.
Feito a especificação do nosso modelo, podemos coletar e tratar nossos dados. Iremos coletar os preços de quatro ações para montar um Equally Weighted Portfolio. Como estamos utilizando ações que estão na B3, iremos utilizar o Índice Bovespa como índice de mercado. Iremos utilizar dados mensais (realizando a transformação de diário para mensal) começando a partir de 2013.
library(tidyverse) library(tidyquant) library(timetk) library(stargazer) library(ggrepel) library(patchwork)
# Define os ativos que irão ser coletados
tickers <- c("PETR4.SA", "ITUB4.SA", "ABEV3.SA", "JBSS3.SA")
# Define a data de início da coleta
start <- "2012-12-01"
# Realiza a coleta dos preços diários
prices <- getSymbols(tickers,
auto.assign = TRUE,
warnings = FALSE,
from = start,
src = "yahoo") %>%
map(~Cl(get(.))) %>%
reduce(merge) %>%
`colnames<-`(tickers)
# Transfroma os preços diários em mensais
prices_monthly <- to.monthly(prices,
indexAt = "lastof",
OHLC = FALSE)
# Calcula os retornos mensais
asset_returns <- Return.calculate(prices_monthly,
method = "log") %>%
na.omit()
# Calcula o portfolio com pesos iguais
portfolio_returns <- Return.portfolio(asset_returns)
# Coleta os dados do ibovespa
getSymbols("^BVSP",
warnings = FALSE,
from = start,
src = "yahoo")
# Calcula os retornos mensais
bvsp_returns <- Ad(BVSP) %>%
to.monthly(indexAt = "lastof",
OHLC = FALSE) %>%
Return.calculate(method = "log") %>%
na.omit() %>%
`colnames<-`("ibovespa")
# Junta os dados
all_returns <- merge.xts(portfolio_returns, bvsp_returns)
Com os nossos dados em mãos, podemos realizar nossa Regressão via MQO.
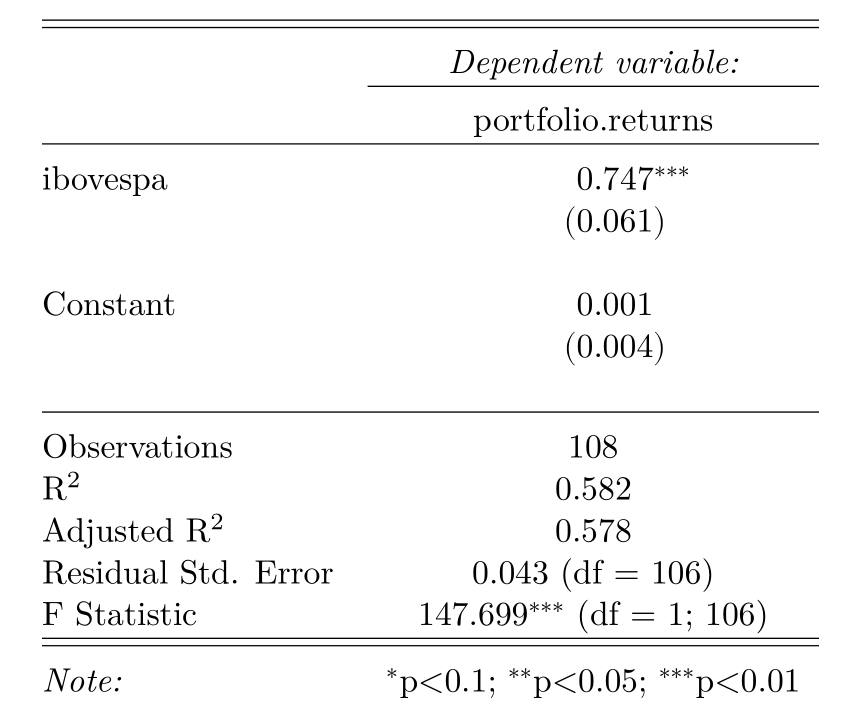
# Cálcula a regressão "estática" market_model <- lm(formula = portfolio.returns ~ ibovespa, data = all_returns) # Cria uma tabela com os resultados da regressão stargazer(market_model, header = FALSE, align = TRUE)
Vemos que tivemos um resultado no qual nosso Beta é menor do 1, significando que nosso portfólio varia menos que o proporcional do mercado.
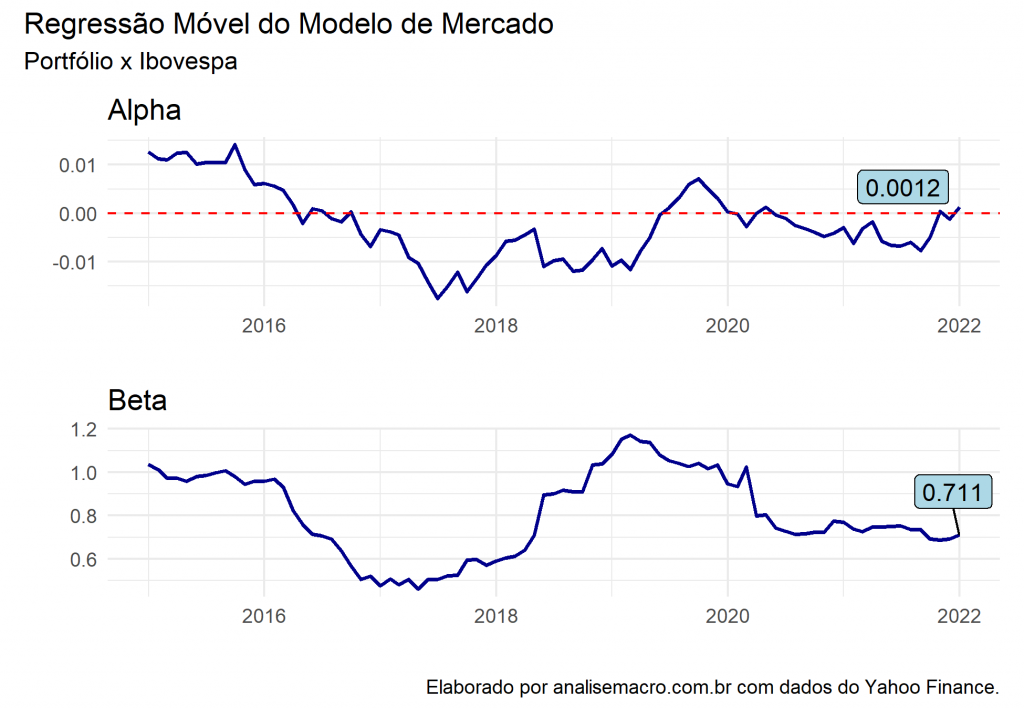
Por fim, sabemos que esse resultado não pode ser o mesmo em todos os horizontes de tempo, para tanto, podemos criar uma Regressão Móvel para saber em quais período de tempo nosso Beta está acima ou abaixo que o proporcional do mercado.
# Aplica a função para criar a regressão móvel
coef <- rollapply(all_returns,
width = 24, # Janela
FUN = function(x) # Cria uma função da regressão para utilizar com a função
{
roll_reg = lm(portfolio.returns ~ ibovespa,
data = as.data.frame(x))
return(roll_reg$coef)
},
by.column = FALSE)
# Limpa e transforma o objeto em tibble
coef_tbl <- coef %>%
na.omit() %>%
tk_tbl(preserve_index = TRUE,
rename_index = "date") %>%
rename(alpha = "X.Intercept.", beta = "ibovespa")
# Cria um gráfico do Alpha móvel
alpha <- ggplot(coef_tbl, aes(x = date, y = alpha))+
geom_line(size = .8, colour = "darkblue")+
theme_minimal()+
labs(title = "Alpha",
x = "",
y = "")+
geom_hline(yintercept = 0, linetype = "dashed", colour = "red")+
geom_label_repel(label = round(tail(coef_tbl$alpha, 1), 4),
nudge_y = 0.002,
nudge_x = -1,
data = tail(coef_tbl, 1),
color = 'black',
fill = 'lightblue')
# Cria um gráfico do Beta móvel
beta <- ggplot(coef_tbl, aes(x = date, y = beta))+
geom_line(size = .8, colour = "darkblue")+
theme_minimal()+
labs(title = "Beta",
x = "",
y = "")+
geom_label_repel(label = round(tail(coef_tbl$beta, 1), 3),
nudge_y = 0.2,
nudge_x = -1,
data = tail(coef_tbl, 1),
color = 'black',
fill = 'lightblue')
# Junta os gráficos
alpha / beta +
plot_annotation(title = "Regressão Móvel do Modelo de Mercado",
subtitle = "Portfólio x Ibovespa",
caption = "Elaborado por analisemacro.com.br com dados do Yahoo Finance.")
(*) Para entender mais sobre Mercado Financeiro e medidas de risco, confira nosso curso de R para o Mercado Financeiro.
________________________