O que é e como calcular o Beta de Mercado usando o Python?

Neste tutorial, explicamos o conceito de Beta de Mercado e como calculá-lo por meio de regressão linear utilizando a linguagem de programação Python. Demonstramos como interpretar graficamente e analisar os parâmetros estimados do método estatístico, contextualizando-o na teoria financeira com um exemplo real. Em seguida, aprofundamos a análise, desenvolvendo um Beta com Janelas Deslizantes e aplicando o modelo CAPM. Por fim, utilizamos a regressão linear múltipla para reproduzir o modelo de três fatores de Fama-French, uma extensão do CAPM.

Introdução

Neste tutorial, explicamos o conceito de Beta de Mercado e como calculá-lo por meio de regressão linear utilizando a linguagem de programação Python. Demonstramos como interpretar graficamente e analisar os parâmetros estimados do método estatístico, contextualizando-o na teoria financeira com um exemplo real. Em seguida, aprofundamos a análise, desenvolvendo um Beta com Janelas Deslizantes e aplicando o modelo CAPM. Por fim, utilizamos a regressão linear múltipla para reproduzir o modelo de três fatores de Fama-French, uma extensão do CAPM.

Regressão Linear e Cálculo do Beta de Mercado

Esta seção explica como a regressão linear é utilizada para calcular o Beta de Mercado, uma medida em finanças que avalia a sensibilidade de uma ação em relação ao mercado.

O que é Regressão Linear?

A regressão linear busca definir o impacto de uma ou mais variáveis independentes em uma variável dependente através de uma equação linear. A equação básica é:

$Y = a + bx + \text{erro}$

Nesta equação:
- $a$ é uma constante, indicando o valor de $Y$ quando $x$ é zero.
- $b$ (beta) é o coeficiente que mede o efeito de uma variação de $x$ em $Y$ .
- O **erro** é a diferença entre o valor observado de $Y$ e o valor estimado, representando as variáveis não incluídas no modelo.

Para melhorar a precisão e reduzir erros devido a variáveis omitidas, podemos adicionar mais variáveis independentes, resultando em uma Regressão Linear Múltipla, expressa por:

$y = \beta_0 + \beta_1x_1 + \beta_2x_2 + \dots + \beta_kx_k + \varepsilon$

Calculando o Beta de Mercado

A observação dos preços das ações revela que, quando o mercado sobe (medido por qualquer índice de bolsa de valores disponível), a maioria das ações tende a aumentar de preço e, quando o mercado cai, a maioria vê seu preço diminuir. Isso sugere que os retornos dos ativos estão correlacionados devido a uma resposta comum às mudanças no mercado.

Modelo de Índice Único

O retorno de uma ação pode ser modelado pela equação:

$R_i = \alpha_i + \beta_i R_m + e_i$

onde:
- $R_i$ é o retorno da ação $i$ .
- $R_m$ é a taxa de retorno do índice de mercado.
- $\beta_i$ é a constante que mede a sensibilidade do retorno da ação ao retorno do mercado.
- $\alpha_i$ representa o retorno adicional obtido além dos fatores de mercado.
- $e_i$ é o termo de erro, com valor esperado zero, refletindo componentes do retorno não sensíveis ao mercado.

O $\beta_i$ é interpretado como uma medida do risco sistemático. Um $\beta_i$ de 2 indica que o retorno da ação deve aumentar (ou diminuir) 2% quando o mercado sobe (ou desce) 1%. Assim, $\beta_i$ mensura a relação do retorno da ação com o mercado.

O Estimador de Mínimos Quadrados

Para estimar os coeficientes desconhecidos do modelo de regressão linear, usamos a técnica de mínimos quadrados ordinários (MQO ou OLS), que minimiza a soma dos quadrados dos erros:

$\sum_{i=1}^n \epsilon_i^2$

O termo de erro $\epsilon$ é a diferença entre os valores observados de $y$ e a estimativa do modelo:

$\epsilon = y - (\beta_0 + \beta_1x)$

Ao minimizar esta soma, encontramos os valores de $\beta_0$ e $\beta_1$ :

$<span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-a9e6a9bef7dcdeb13da3365bf395b03f_l3.png" height="69" width="206" class="ql-img-displayed-equation quicklatex-auto-format" alt="\begin{align*} \beta_0 & = \bar{y} - \beta_1 \bar{x} \\ \beta_1 & = \frac{\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^n (x_i - \bar{x})^2} \end{align*}" title="Rendered by QuickLaTeX.com"/>$

onde $\bar{y}$ e $\bar{x}$ são as médias amostrais de $y$ e $x$ , respectivamente. Este processo é aplicado para calcular o $\beta$ de mercado, usando o retorno de uma ação como $y$ e o retorno do mercado como $x$ .

Não precisamos nos preocupar com o cálculo manual, afinal, o Python irá nos ajudar nessa tarefa.

Regressão Linear no Python usando statsmodels

No Python, para criar a regressão, utilizaremos a função ols() da biblioteca statsmodels e de seu API formula.api.

Vamos analisar a relação entre o retorno mensal de uma ação, neste caso, PETR4 (embora o mesmo processo possa ser aplicado a qualquer outra ação listada na bolsa de valores), e o retorno do Índice Bovespa. Nosso objetivo é entender se o retorno mensal do índice, que representa o desempenho geral do mercado, influencia o retorno diário da ação.

Para começar, vamos importar os dados e calcular os retornos necessários para a análise.

Vamos criar a regressão utilizando a função smf.ols, onde passaremos a fórmula como argumento, especificando o modelo. Para estimar os parâmetros do modelo, utilizamos o método fit(), e para visualizar os resultados detalhados da regressão, usamos o método summary().

                            OLS Regression Results                            
==============================================================================
Dep. Variable:                   petr   R-squared:                       0.643
Model:                            OLS   Adj. R-squared:                  0.640
Method:                 Least Squares   F-statistic:                     202.0
Date:                Wed, 06 Nov 2024   Prob (F-statistic):           7.93e-27
Time:                        07:42:07   Log-Likelihood:                 125.64
No. Observations:                 114   AIC:                            -247.3
Df Residuals:                     112   BIC:                            -241.8
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const          0.0038      0.008      0.491      0.624      -0.011       0.019
ibov           1.6638      0.117     14.212      0.000       1.432       1.896
==============================================================================
Omnibus:                       13.387   Durbin-Watson:                   1.758
Prob(Omnibus):                  0.001   Jarque-Bera (JB):               17.676
Skew:                           0.623   Prob(JB):                     0.000145
Kurtosis:                       4.473   Cond. No.                         15.4
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Vamos realizar a leitura dos parâmetros estimados:

Obs. os valores estimados podem mudar caso ocorra alterações no período da amostra de dados.

Beta (ibov): O coeficiente de 1,6638 significa que, para cada variação de 1% no IBOV, espera-se que o retorno da PETR4 varie, em média, 1,6638%. Como o beta é maior que 1, a PETR4 é mais volátil que o mercado. Em outras palavras, a ação tende a se mover mais que o IBOV, indicando que ela é relativamente mais sensível às variações do mercado.
Constante (const): O valor 0,0038 sugere que, quando o IBOV não varia, o retorno médio da PETR4 seria de aproximadamente 0,38% por período analisado. Porém, este valor não é estatisticamente significativo, como mostrado pelo p-valor (0.624), o que significa que não há evidências fortes para afirmar que esse retorno médio é diferente de zero.
R-quadrado (R-squared): O valor de 0,643 indica que aproximadamente 64,3% da variação nos retornos da PETR4 pode ser explicada pelas variações no IBOV. Isso sugere que existe uma forte relação entre PETR4 e IBOV, mas ainda assim, cerca de 35,7% da variação nos retornos de PETR4 é explicada por outros fatores não capturados por este modelo.
Estatística F (F-statistic): Com um valor de 202,0 e um p-valor de 7,93e-27, a estatística F indica que o modelo como um todo é altamente estatisticamente significativo. Ou seja, o IBOV é uma variável muito relevante para explicar o comportamento da PETR4.
t-Estatística e p-valor: O t-valor de 14,212 e o p-valor de 0,000 para o coeficiente do IBOV mostram que o beta é estatisticamente muito significativo, ou seja, há uma forte relação significativa entre IBOV e PETR4.

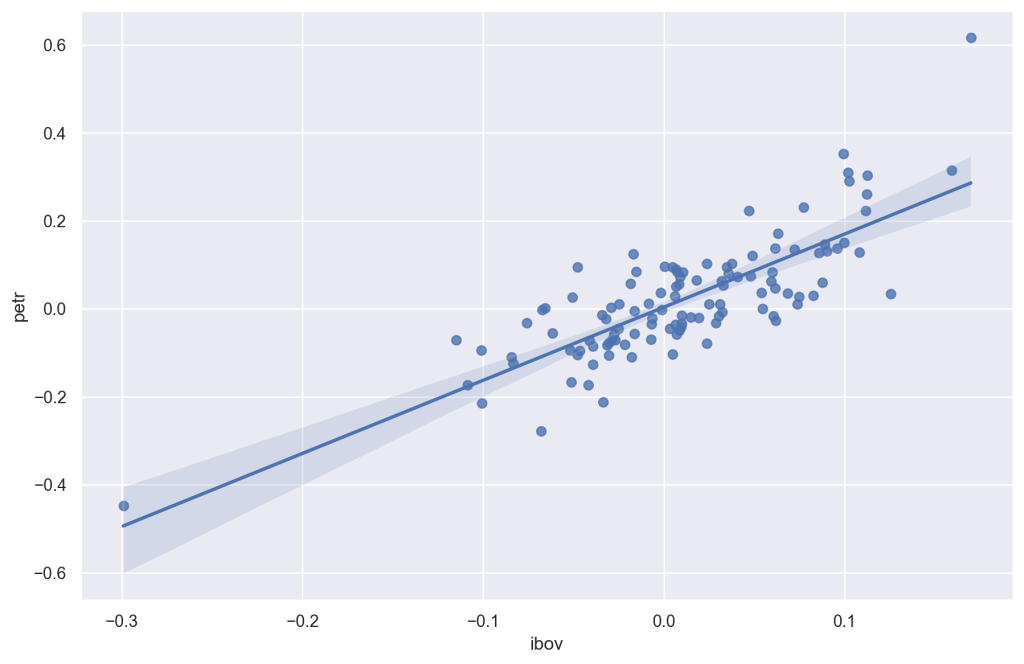
Como visualizar?

Para representar a relação entre as duas variáveis usamos um gráfico de dispersão com reta de regressão, onde no eixo x é inserido os valores dos retornos do ibovespa e no eixo y os valores dos retornos da PETR4.

Regressão em Janelas Deslizantes

Anteriormente, estimamos o Beta da Ação PETR4 utilizando toda a amostra de dados, resultando em um único valor fixo.

Problema: As relações em séries temporais podem variar ao longo do tempo, pois raramente permanecem estáticas. Além disso, dados muito antigos podem ter pouca relevância na explicação do presente ou futuro. Para lidar com essas mudanças, é necessário aplicar uma técnica que considere essa variação temporal.

Janelas Deslizantes (Rolling Windows): Essa técnica cria uma amostra fixa que se “desliza” ao longo do tempo, permitindo observar um subconjunto de dados em períodos específicos. Ao definir o tamanho da janela (quantidade de observações na amostra fixa), a observação mais antiga é removida à medida que uma nova é adicionada. Isso é semelhante a analisar um grupo de meses de cada vez e mover essa “janela” continuamente ao longo da série temporal.

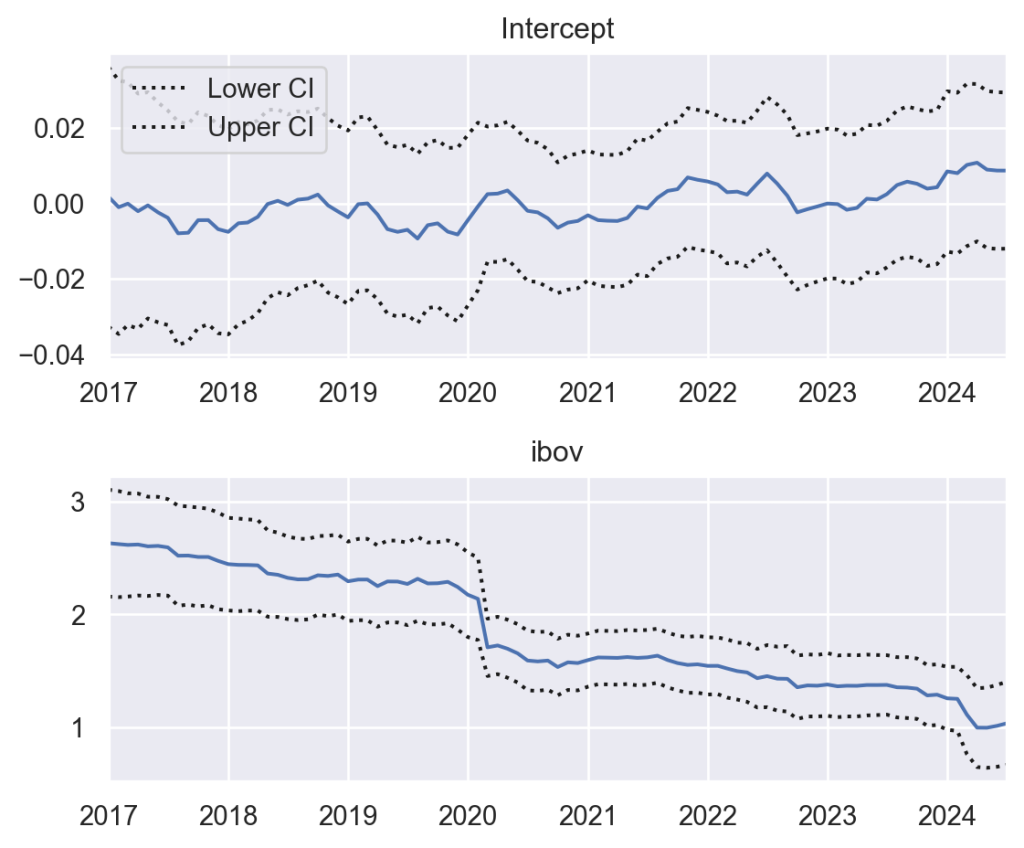
Ao aplicar Janelas Deslizantes na Regressão Linear, geramos uma série temporal dos parâmetros estimados, como o Beta de Mercado. Isso possibilita identificar como a sensibilidade do ativo ao mercado evolui ao longo do tempo, capturando mudanças e eventos específicos.

Para implementar essa abordagem com o statsmodels, podemos utilizar o módulo RollingOLS.

O Modelo CAPM (Capital Asset Pricing Model)

O CAPM é uma extensão do modelo de índice único que oferece uma visão mais abrangente do retorno esperado de um ativo. A equação do CAPM é:

$R_i = R_f + \beta_i (R_m - R_f)$

onde:
- $R_i$ é o retorno esperado da ação $i$ .
- $R_f$ é a taxa de retorno livre de risco (ou taxa de juro de um ativo sem risco).
- $R_m$ é o retorno esperado do mercado.
- $\beta_i$ é o Beta da ação, que mede a sensibilidade do retorno da ação em relação ao retorno do mercado.

Diferença entre o CAPM e o Modelo de Índice Único

Taxa Livre de Risco:
- Modelo de Índice Único: Não considera uma taxa livre de risco. O retorno da ação é modelado diretamente como uma função do retorno do mercado.
- CAPM: Inclui a taxa livre de risco ( $R_f$ ), que representa o retorno esperado de um ativo sem risco. Isso permite calcular o retorno esperado da ação com base na relação entre o risco da ação e o retorno do mercado.
Retorno Esperado:
- Modelo de Índice Único: Foca na relação entre o retorno da ação e o retorno do índice de mercado, sem uma referência ao retorno livre de risco.
- CAPM: Calcula o retorno esperado da ação levando em consideração a taxa livre de risco e o prêmio de risco do mercado ( $R_m - R_f$ ).
Compreensão do Risco:
- Modelo de Índice Único: Assume que a única fonte de risco sistemático é o retorno do mercado.
- CAPM: Amplia o conceito de risco sistemático ao incluir a taxa livre de risco e calcular o prêmio de risco necessário para compensar o risco da ação.

Aplicação Prática

Ambos os modelos utilizam o Beta ( $\beta_i$ ) para medir a sensibilidade da ação ao mercado, mas o CAPM fornece uma fórmula para calcular o retorno esperado com base no risco sistemático. Enquanto o modelo de índice único é útil para entender a relação básica entre uma ação e o mercado, o CAPM oferece uma ferramenta mais completa para avaliação de investimentos, considerando o retorno livre de risco e o prêmio de risco.

Vamos agora aplicar esses conceitos em um exemplo prático para ilustrar a diferença entre o modelo de índice único e o CAPM na avaliação de uma ação.

                            OLS Regression Results                            
==============================================================================
Dep. Variable:            petr_excess   R-squared:                       0.643
Model:                            OLS   Adj. R-squared:                  0.639
Method:                 Least Squares   F-statistic:                     201.4
Date:                Wed, 06 Nov 2024   Prob (F-statistic):           8.87e-27
Time:                        07:42:21   Log-Likelihood:                 125.51
No. Observations:                 114   AIC:                            -247.0
Df Residuals:                     112   BIC:                            -241.5
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
===============================================================================
                  coef    std err          t      P>|t|      [0.025      0.975]
-------------------------------------------------------------------------------
Intercept       0.0087      0.008      1.136      0.258      -0.006       0.024
ibov_excess     1.6599      0.117     14.190      0.000       1.428       1.892
==============================================================================
Omnibus:                       14.480   Durbin-Watson:                   1.754
Prob(Omnibus):                  0.001   Jarque-Bera (JB):               19.635
Skew:                           0.658   Prob(JB):                     5.45e-05
Kurtosis:                       4.550   Cond. No.                         15.4
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified. Através da fórmula do CAPM, encontramos o seguinte resultado para o alvo do retorno mensal da PETR4: O Retorno Esperado Mensal da Petr4 é de: 1.343%

Regressão Linear Múltipla

Modelo de 3 Fatores de Fama-French

O Modelo de 3 Fatores é uma extensão do CAPM que introduz fatores adicionais para explicar os retornos dos ativos. Este modelo foi desenvolvido para capturar riscos adicionais que não são explicados pelo CAPM.

Modelo de 3 Fatores

Equação Básica:

$R_i = R_f + \beta_i (R_m - R_f) + s_i SMB + h_i HML + e_i$

onde:
- $R_i$ é o retorno da ação $i$ .
- $R_f$ é a taxa livre de risco.
- $R_m$ é o retorno do mercado.
- $SMB$ (Small Minus Big) é o fator que captura o tamanho da empresa.
- $HML$ (High Minus Low) é o fator que captura o valor versus crescimento.
- $\beta_i, s_i, h_i$ são os coeficientes de sensibilidade.
- $\alpha_i$ é o retorno adicional.
- $e_i$ é o erro.

Pontos importantes sobre os fatores:

- O fator SMB representa a diferença de desempenho entre ações de empresas pequenas (small caps) e grandes (big caps). Historicamente, ações de empresas menores têm maior potencial de crescimento, mas também são mais voláteis e arriscadas. O prêmio SMB reflete o retorno adicional esperado por investir em small caps em vez de big caps.

- O fator HML captura a diferença de desempenho entre ações de empresas com altos valores contábeis em relação ao preço de mercado (high book-to-market, frequentemente associadas a “valor”) e aquelas com baixos valores contábeis em relação ao preço (low book-to-market, frequentemente associadas a “crescimento”).
- Empresas high book-to-market (valor) geralmente têm características como maior estabilidade, dividendos regulares e crescimento moderado, enquanto empresas low book-to-market (crescimento) podem ter alta valorização potencial, mas também maior risco

                            OLS Regression Results                            
==============================================================================
Dep. Variable:            petr_excess   R-squared:                       0.769
Model:                            OLS   Adj. R-squared:                  0.763
Method:                 Least Squares   F-statistic:                     122.0
Date:                Wed, 06 Nov 2024   Prob (F-statistic):           7.51e-35
Time:                        07:42:22   Log-Likelihood:                 150.40
No. Observations:                 114   AIC:                            -292.8
Df Residuals:                     110   BIC:                            -281.9
Df Model:                           3                                         
Covariance Type:            nonrobust                                         
===============================================================================
                  coef    std err          t      P>|t|      [0.025      0.975]
-------------------------------------------------------------------------------
Intercept      -0.0062      0.006     -0.963      0.338      -0.019       0.007
Rm_minus_Rf     1.4056      0.118     11.915      0.000       1.172       1.639
SMB            -0.1414      0.136     -1.041      0.300      -0.410       0.128
HML             0.8883      0.109      8.145      0.000       0.672       1.104
==============================================================================
Omnibus:                        8.944   Durbin-Watson:                   1.994
Prob(Omnibus):                  0.011   Jarque-Bera (JB):               15.516
Skew:                           0.272   Prob(JB):                     0.000427
Kurtosis:                       4.724   Cond. No.                         25.6
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

R-squared (R²): 0.769
- Indica que aproximadamente 76.9% da variabilidade do retorno excessivo da PETR4 é explicada pelo modelo de três fatores de Fama-French.
F-statistic: 122.2 (Prob > F: 7.04e-35)
- Testa se o modelo como um todo é estatisticamente significativo. O p-valor muito pequeno indica que o modelo é estatisticamente significativo e explica uma porção significativa da variação no retorno excessivo da PETR4.
AIC e BIC
- Medidas usadas para comparar modelos: menores valores sugerem um modelo melhor ajustado considerando a penalização por complexidade.

Coeficientes dos Fatores

Intercepto: -0.0068 (p-valor: 0.293)
- Representa o alfa do modelo, ou seja, o retorno anormal da PETR4 que não é explicado pelos três fatores. Como o p-valor é alto (0.293), não é estatisticamente significativo, indicando que o retorno anormal não é significativamente diferente de zero.
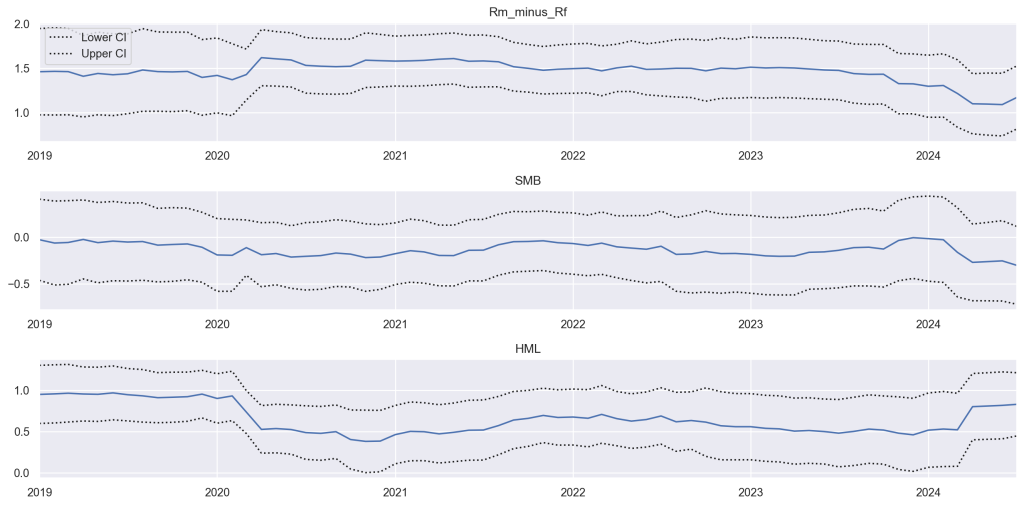
Rm_minus_Rf (Prêmio de Mercado): 1.4096 (p-valor: 0.000)
- Teoricamente, este fator mede o prêmio de risco do mercado. O coeficiente de 1.4096 indica que para cada unidade de prêmio de risco do mercado, o retorno excessivo da PETR4 aumenta em 1.4096 unidades. O p-valor extremamente baixo (0.000) indica que este fator é altamente significativo para explicar os retornos da PETR4.
SMB (Small Minus Big): -0.1352 (p-valor: 0.322)
- O coeficiente negativo (-0.1352) sugere que a PETR4 se comporta de maneira oposta às small caps, exibindo características de uma ação de grande capitalização. A magnitude do coeficiente (0.1352) é relativamente pequena e, com um p-valor de 0.322, o impacto do fator SMB não é estatisticamente significativo. Isso implica que o retorno excessivo da PETR4 não é fortemente influenciado por dinâmicas de capitalização de mercado (tamanho da empresa).
- Implicação: Investidores que buscam exposição ao fator de tamanho não encontrariam na PETR4 um retorno significativo baseado neste prêmio. A PETR4 se alinha mais com o perfil de grandes empresas, para as quais o fator SMB não adiciona valor relevante aos retornos esperados.
HML (High Minus Low): 0.8867 (p-valor: 0.000)
- O coeficiente positivo (0.8867) indica que a PETR4 se comporta de maneira semelhante a ações de valor, que tendem a ter altos valores contábeis em relação aos preços de mercado. O retorno excessivo da PETR4 aumenta significativamente com o prêmio de valor, refletindo uma alta sensibilidade a este fator.
- Com p-valor significativo reforça que o fator HML é um determinante para os retornos da PETR4. Isso pode estar relacionado à percepção de que PETR4, como uma grande empresa de commodities (petróleo e gás), exibe características de empresas de valor, tais como ativos substanciais e uma estrutura de negócios mais estabelecida e menos centrada em crescimento acelerado.
- Implicação: Investidores interessados em exposição ao fator de valor encontram na PETR4 uma ação alinhada com suas preferências, aproveitando a resiliência associada às ações high book-to-market. A PETR4 parece oferecer um retorno compensatório por estar vinculada a ativos tangíveis e fundamentos fortes, características típicas de ações de valor.

Referências

Fabozzi, F. J., & Markowitz, H. M. (2002). The theory and practice of investment management. Second Edition. John Wiley & Sons.

Elton, E., Gruber, M., & Brown, S. (2012). Moderna teoria de carteiras e análise de investimentos. Elsevier Brasil.

Tenha acesso ao código e suporte desse e de mais 500 exercícios no Clube AM!

Quer o código desse e de mais de 500 exercícios de análise de dados com ideias validadas por nossos especialistas em problemas reais de análise de dados do seu dia a dia? Além de acesso a vídeos, materiais extras e todo o suporte necessário para você reproduzir esses exercícios? Então, conheça o Clube AM clicando aqui.

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais
e conteúdos exclusivos sobre Análise de Dados!

Assinar

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Criando um Dashboard de Análise de Dados de Demonstrativos Financeiros no Python

IPCA de outubro surpreende mercado, mas fica em linha com a previsão da Análise Macro

Análise dos Preços de Combustíveis usando o Python

Uma introdução à Inteligência Artificial e a Engenharia de Prompt

Como identificar mensagens de erro na coleta de dados de sites públicos

O que é e como calcular o Beta de Mercado usando o Python?

Outros artigos relacionados

Criando um Dashboard de Análise de Dados de Demonstrativos Financeiros no Python

Este projeto demonstra como criar um dashboard para análise de dados das demonstrações financeiras de empresas brasileiras, utilizando dados disponibilizados pela CVM. Desenvolvemos o dashboard com Python e Shiny, permitindo a coleta, tratamento e análise dos dados diretamente na interface.

IPCA de outubro surpreende mercado, mas fica em linha com a previsão da Análise Macro

O IBGE divulgou recentemente os dados de inflação de outubro/2024. A previsão da Análise Macro em 14 de setembro era de um aumento do IPCA em 0,48% para o mês de outubro, com viés altista, enquanto que o indicador mostrou uma variação de 0,56%, puxado por despesas com habitação. Por sua vez, a previsão de mercado em 13 de setembro era de 0,31% de aumento na inflação, de acordo com o relatório Focus/BCB.

Análise dos Preços de Combustíveis usando o Python

Neste exercício, realizamos uma análise dos preços de combustíveis no Brasil, utilizando Python para todo o processo de coleta, tratamento, ajuste pela inflação, cálculo de médias e visualização dos dados.

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!