Como avaliar a relação de risco-retorno de ações no Python

Por que Avaliar a Relação de Risco-Retorno de Ações no Python?

A relação entre risco e retorno é um dos conceitos centrais na prática de gestão de investimentos. Avaliar essa relação corretamente permite que investidores e gestores de portfólio tenham sucesso e consistência na obtenção de retornos no mercado financeiro a um custo de risco mínimo.

Neste artigo, mostramos como analisar risco-retorno utilizando Python. A linguagem permite automatizar todas as etapas: da coleta de dados ao tratamento, cálculo e visualização.

Além de ser gratuita, o Python oferece alto grau de customização. Isso a torna uma excelente escolha para investidores individuais, profissionais institucionais e pesquisadores acadêmicos em finanças quantitativas.

Por que entender a relação de risco-retorno?

Ao investir em ações, é fundamental compreender o equilíbrio entre o potencial de retorno e o risco assumido. Essa relação de risco-retorno é a base para decisões racionais de investimento, pois ajuda a identificar oportunidades mais eficientes, ou seja, aquelas que oferecem maior retorno para um dado nível de risco.

Vantagens do uso do Python para análise de risco-retorno

Muitos investidores recorrem a plataformas pagas e limitadas em termos de customização. O Python, por outro lado, permite:

Análises personalizadas;
Reprodutibilidade e automatização;
Custo zero;
Flexibilidade para testes e simulações.

Essas características tornam a linguagem especialmente útil para quem busca entender a fundo a dinâmica do risco-retorno em ativos financeiros.

Objetivos deste tutorial

Ao final deste passo a passo, você será capaz de:

Construir carteiras eficientes com base em diferentes restrições;
Avaliar a performance da carteira frente a benchmarks como a renda fixa ou o Ibovespa;
Medir e gerir o risco da carteira de forma estruturada.

Para obter o código e o tutorial deste exercício faça parte do Clube AM e receba toda semana os códigos em R/Python, vídeos, tutoriais e suporte completo para dúvidas.

Primeiros passos: dados de preços

Vamos iniciar o processo capturando os preços históricos de quatro ações da bolsa brasileira, além do índice bovespa, que funcionará como benchmark para comparação de desempenho. Os dados são obtidos por meio do Python através da biblioteca yfinance, que possibilita extrair dados de preços de ações do site Yahoo Finance.

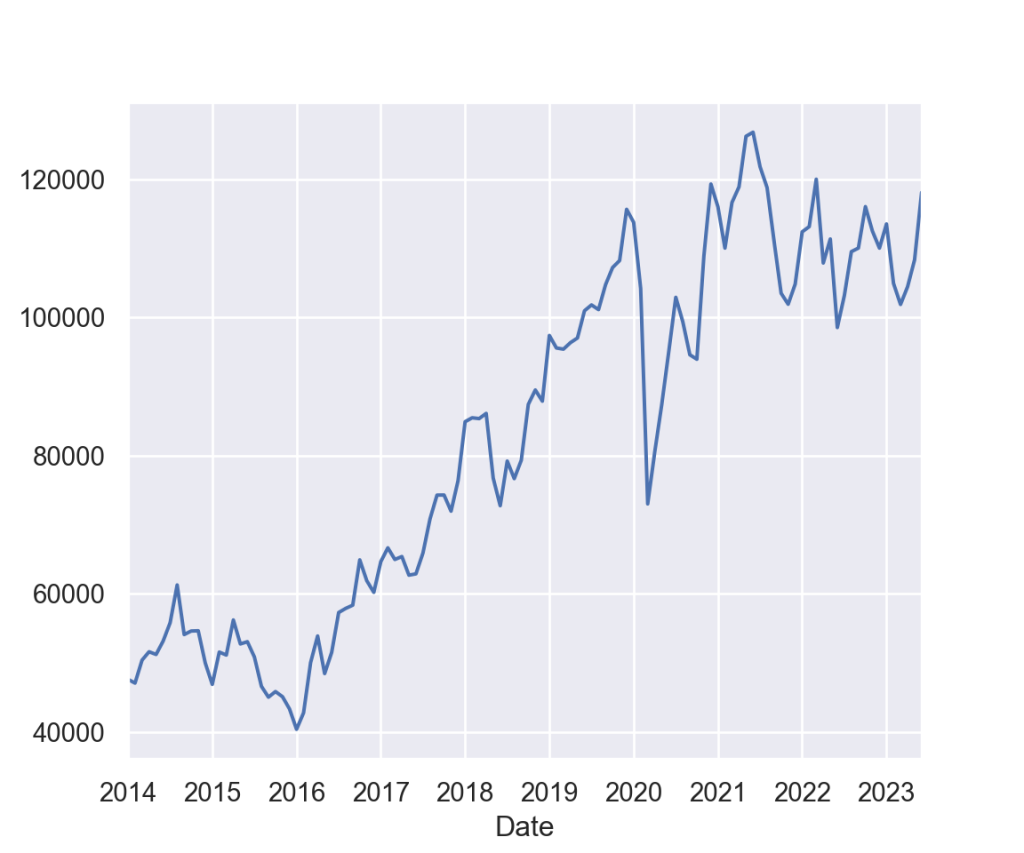
Realizamos a coleta de dados da série de preços de fechamento mensal do Ibovespa no período de 2014 até fim de 2023. Com o Python, podemos realizar diversos cálculos e análises visuais. Assim construímos o gráfico desta série temporal.

Ao observar a série de preços de fechamento mensal do Ibovespa, notamos um comportamento errático e, durante o período analisado, sem uma tendência clara. No entanto, preços brutos (ou pontos no caso do índice) pouco informam sobre a real performance de um ativo. O que realmente importa para o gestor de carteiras são os retornos diários.

Antes de avançarmos com a mensuração da relação risco-retorno, vamos entender o conceito de retorno.

O que é retorno e como calculá-lo no Python?

Para avaliar a relação de risco-retorno de uma ação, precisamos primeiro transformar os preços dos ativos em retornos. Afinal, são os retornos que indicam o quanto um ativo está se valorizando (ou desvalorizando) ao longo do tempo — e, portanto, são a base para qualquer análise de performance ou risco.

Retorno discreto

A forma mais simples e intuitiva de calcular o retorno de um ativo financeiro é através da variação percentual do preço entre dois períodos consecutivos:

$R_{t,disc}=\frac{P_{t}-P_{t-1}}{P_{t-1}}= \Delta P_t\%$

Onde o retorno de um período (dia), $R_{disc}$ , é a diferença entre o preço $P$ no período $t$ (por exemplo, hoje) e o preço $P$ no período $t-1$ (por exemplo, ontem) dividido pelo preço em $t-1$ . Isto nos dá a variação percentual $\Delta P_t\%$ do ativo.

Retorno contínuo (log-retorno)

Contudo, na prática financeira e acadêmica, é comum utilizarmos o retorno contínuo, também chamado de log-retorno, definido da seguinte forma:

$R_{t,cont} = ln\left(\frac{P_t}{P_{t-1}}\right)=ln(P_t)-ln(P_{t-1})\approx \Delta P_t\%$

Então o log-retorno, $R_{t,cont}$ , é igual ao logaritimo natural do preço de hoje dividido pelo preço de ontem. Pelas propriedade do log natural, isto é igual a diferença dos logs dos preços, que é aproximadamente igual aos retornos discretos.

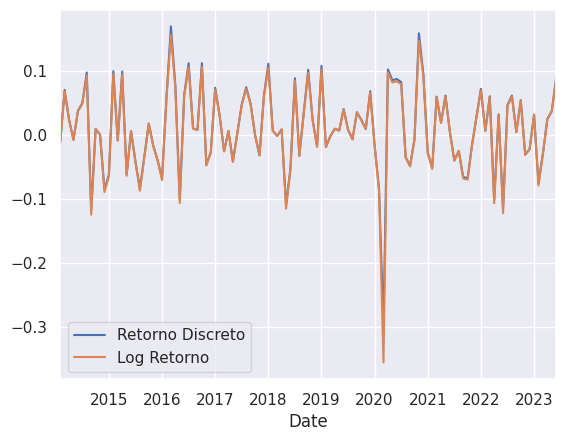
Embora ambos os métodos produzam resultados semelhantes em intervalos curtos, o log-retorno possui várias vantagens técnicas:

Aditividade no tempo: os log-retornos podem ser somados diretamente para formar o retorno acumulado em períodos maiores. Isso facilita análises com frequência diária, semanal ou mensal.
Distribuição estatística mais próxima da normal: para muitos ativos, os log-retornos apresentam uma distribuição mais simétrica, o que melhora a aplicação de modelos estatísticos.
Simplicidade matemática em modelos contínuos: modelos como o de Black-Scholes e outros da matemática financeira utilizam log-retornos por serem mais adequados à modelagem estocástica contínua.
Estabilidade computacional: ao trabalhar com grandes variações ou séries longas, o uso de logaritmos reduz erros numéricos e melhora a interpretação dos resultados.

Agora vamos, de fato, calcular os retornos:

Assim, transformamos a série de nível para retornos.

Agora é possível analisar as estatísticas descritivas para checarmos as características dos retornos das ações e do Ibovespa.

Em qualquer exercício empírico é interessante estudar as estatísticas básicas da variável com a qual você vai trabalhar. Para a gestão de portfólio, é importante analisar a média, variância e desvio-padrão do ativo (veremos mais adiante o porquê). Para outros trabalhos em finanças, principalmente na área de risco, pode ser muito importante estudar a assimetria (skewness) e a curtose da série também.

Com o uso do Python, conseguimos obter os seguintes resultados para as estatísticas descritivas.

	BBDC4.SA	GGBR4.SA	ITSA4.SA	WEGE3.SA	^BVSP
count	113.000000	113.000000	113.000000	113.000000	113.000000
mean	0.008081	0.007260	0.010452	0.021250	0.008033
std	0.099825	0.138298	0.084569	0.083522	0.068500
min	-0.382640	-0.521515	-0.297199	-0.247675	-0.355310
25%	-0.057746	-0.060950	-0.038860	-0.030257	-0.029497
50%	0.008238	0.001875	0.010431	0.024981	0.008016
75%	0.081117	0.089704	0.067764	0.068778	0.058242
max	0.238493	0.616639	0.219500	0.286519	0.156724
skewness	-0.417216	0.081657	-0.423073	-0.011801	-1.287475
kurtosis	4.206233	6.866079	3.752788	3.994447	8.614712

Vemos que em 113 observações, o mínimo e o máximo registrados do Ibovespa foram de -0.355310 e 0.156724 e a média foi de 0.008033.

Também é possível perceber que existe assimetria (skewness) negativa de -1.287475 e que a série é leptocurtica, pois há uma curtose em excesso de 8.614712.

A curtose de uma distribuição Normal é de 3 (para a definição de Pearson, para a definição de Fisher, a curtose de uma normal é 0).

Isto quer dizer que, existem mais retornos negativos do que positivos (assimetria negativa) e que eventos extremos são mais comuns do que o normal (curtose em excesso).

Estas duas últimas características são muito comuns em séries financeiras e indicam uma possível não-Normalidade dos dados. Esta constatação é importante especialmente para análise de risco avançada. Porém, dado o caráter introdutório do tutorial, quando necessário, vamos adotar a hipótese simplificadora de que os retornos são Normais.

Boa parte do mercado ainda trabalha desta maneira e até mesmo a literatura indica que em alguns casos a hipótese de normalidade não é tão forte assim.

Retorno-Risco

Em uma descrição livre, é possível separar a gestão de portfólio em quatro grandes processos dinâmicos:

escolha dos ativos que o investidor deseja ter em carteira (tipicamente escolhido por técnicas de análise macro, fundamentalista, técnica ou quantitativa);
otimização, isto é, a escolha da melhor carteira – o quanto investir em cada ativo (para maximizar a razão retorno/risco);
análise da performance da carteira;
gestão do risco (tipicamente modelagem e previsão da probabilidade de perda financeira).

Vamos assumir que após algum processo de análise, o gestor selecionou as ações do Bradesco (BBDC4), Itaúsa (ITSA4), Gerdau (GGBR4) e Wege (WEGE3). O foco será calcular os retornos e mensurar a relação de risco.

Entretanto, ainda devemos definir alguns conceitos importantes para a gestão de carteiras.

Retorno-Risco de Ativos Individuais

No contexto de gestão de carteiras, os ativos individuais são caracterizados por duas dimensões: retorno e risco. O retorno, neste tutorial, é tratado como a média amostral dos retornos de um ativo durante um certo período de tempo.

Formalmente:

$\bar{R}_{i} = \frac{\sum_{t=1}^T (R_{it})}{T}$

Então, o retorno esperado do ativo $i$ , $\bar{R}_i$ é igual a soma de todos os retornos do ativo $\sum_{t=1}^T(R_i)$ dividido pelo número de observações, $T$ .

Tomemos o Ibovespa como exemplo prático, novamente. Para calcular sua média amostral, isto é, o retorno esperado basta utilizarmos o método mean, disponível para os DataFrames do pandas no Python. O resultado pode ser visto abaixo:

BBDC4.SA    0.008081
GGBR4.SA    0.007260
ITSA4.SA    0.010452
WEGE3.SA    0.021250
^BVSP       0.008033
dtype: float64

O risco, nesta tutorial, é tido como a variância amostral ou o desvio padrão da série de retorno do ativo. Formalmente:

$\sigma_i^2= \frac{\sum_{t=1}^T(R_{it}-\bar{R}_i)^2}{T-1}$

Onde, $\sigma_i^2$ é a variância do ativo $i$ , que é a soma das diferenças ao quadrado.

O valor da variância, contudo, não é facilmente interpretado. Por isso, em exercícios práticos é muito comum usarmos o desvio-padrão como a métrica de risco.

$\sigma_i= \sqrt{\frac{\sum_{t=1}^T(R_{it}-\bar{R}_i)^2}{T-1}}$

O desvio-padrão $\sigma_i$ é simplesmente a raiz quadrada da variância. A vantagem desta métrica é que ela pode ser intepretada em termos deporcentagem. Assim, um desvio-padrão de 20%, por exemplo, significa que o ativo varia normalmente 20% em torno do retorno esperado.

Em termos um pouco mais formais, assumindo uma distribuição Normal, há uma probabilidade de 68\% de os retornos do ativo variarem 20\% em torno da média. Ou seja, com probabilidade de 68\% os retornos estarão na faixa de $R_i - \sigma_i$ e $R_i + \sigma_i$

No caso dos retornos, temos a variância com o seguinte resultado:

BBDC4.SA    0.009965
GGBR4.SA    0.019126
ITSA4.SA    0.007152
WEGE3.SA    0.006976
^BVSP       0.004692
dtype: float64

E para o desvio-padrão:

BBDC4.SA    0.099825
GGBR4.SA    0.138298
ITSA4.SA    0.084569
WEGE3.SA    0.083522
^BVSP       0.068500
dtype: float64 

Ambos os resultados produzidos facilmente com os métodos disponíveis no DataFrame do pandas no Python.

Retorno-Risco de Carteiras e o Papel da Diversificação

Ao investir, raramente nos limitamos a um único ativo. Combinamos diferentes ativos para formar uma carteira — uma estratégia central na gestão de risco e retorno. Quando fazemos isso, estamos criando, na prática, um novo ativo: a carteira. Esta carteira possui características próprias de retorno e risco, que não são simples médias dos ativos que a compõem.

O retorno esperado de uma carteira é uma média ponderada dos retornos dos ativos. Suponha dois ativos A e B, com retornos médios de 10% e 20%, respectivamente. Se decidirmos alocar 40% do capital em A e 60% em B, o retorno esperado da carteira será:

$\bar{R}_p = 0{,}4 \times 10\% + 0{,}6 \times 20\% = 4\% + 12\% = 16\%$

Note que esse retorno está entre os retornos individuais dos ativos. Isso sempre ocorre, pois estamos lidando com uma combinação convexa, ou seja, uma média ponderada. Assim, o retorno da carteira será sempre menor ou igual ao maior retorno individual. Surge então a pergunta: por que não investir tudo no ativo com maior retorno?

A resposta está no risco. Suponha que o ativo B seja muito mais volátil do que A — isto é, apresente maior incerteza em seus retornos. Ao investir exclusivamente em B, você estaria se expondo totalmente a esse risco. Ao diversificar, combinando A e B, o retorno pode ser um pouco menor, mas o risco da carteira pode ser significativamente reduzido. Essa é a essência da diversificação.

Para entender melhor essa redução de risco, precisamos explorar como se calcula o risco de uma carteira. Diferente do retorno, o risco (medido como desvio padrão dos retornos) não é uma média ponderada simples. A fórmula leva em consideração não só a variância individual de cada ativo, mas também como os ativos se relacionam entre si — ou seja, sua covariância.

A fórmula para o desvio padrão de uma carteira com dois ativos A e B é:

$\sigma_P = \sqrt{w_A^2\sigma_A^2 + w_B^2\sigma_B^2 + 2w_Aw_B\sigma_{AB}}$

Aqui, $\sigma_A$ e $\sigma_B$ são os desvios padrão dos ativos individuais, e $\sigma_{AB}$ é a covariância entre eles — ou seja, uma medida de como os dois ativos se movem juntos.

A covariância é dada por:

$\sigma_{AB} = \frac{1}{T-1} \sum_{t=1}^T (R_{At} - \bar{R}_A)(R_{Bt} - \bar{R}_B)$

Se essa covariância for positiva, os ativos tendem a subir e cair juntos. Se for negativa, quando um sobe, o outro tende a cair, o que pode ajudar a equilibrar a carteira. Portanto, ao incluir ativos com covariância negativa ou baixa, conseguimos reduzir o risco total, mesmo mantendo um retorno atrativo.

Como a covariância é uma medida difícil de interpretar em termos absolutos, usamos frequentemente a correlação:

$\rho_{AB} = \frac{\sigma_{AB}}{\sigma_A \sigma_B}$

A correlação varia de -1 a 1:

Se $\rho = 1$ , os ativos se movem exatamente juntos.
Se $\rho = 0$ , não têm relação linear.
Se $\rho = -1$ , movem-se em direções opostas.

Quanto menor a correlação, maior o potencial de diversificação. Por exemplo, se você investe em dois ativos com correlação próxima de 1, ao cair um, o outro tende a cair junto. Já se a correlação for negativa, uma queda em A pode ser compensada por uma alta em B, suavizando o comportamento da carteira como um todo.

Em resumo, o benefício da diversificação não está apenas em diluir o capital entre ativos, mas em combinar ativos que não se movem perfeitamente juntos. Ao fazer isso, é possível reduzir o risco sem necessariamente reduzir o retorno. Esse é o ponto-chave da eficiência de portfólio: construir combinações de ativos que maximizam o retorno esperado para um dado nível de risco, ou minimizam o risco para um dado retorno.

Esse conceito é a base da moderna teoria de portfólios, e será aprofundado ao tratarmos da fronteira eficiente e dos métodos de otimização de carteiras.

Notação Matricial do Cálculo de Portfólio

Para facilitar o cálculo, podemos usar a notação matricial (para dois ativos), como segue:

$\sigma^2_{P} = \begin{bmatrix}{w_1 w_2}\end{bmatrix} \begin{bmatrix}{\sigma^2_1} &{\sigma_{1,2}} \\[0.3em] {\sigma_{2,1}} & {\sigma^2_2}\end{bmatrix} \begin{bmatrix}{w_1} \\{w_2}\end{bmatrix}$

A partir dessa notação, podemos facilmente realizar o cálculo no Python.

Relação de Risco-Retorno

No contexto da teoria moderna do portfólio, partimos da premissa de que os investidores são racionais: ao escolherem entre diferentes ativos, buscam sempre maximizar o retorno esperado e minimizar o risco associado.

Isso nos leva a um conceito central na análise de investimentos: a relação risco-retorno. Trata-se da maneira como avaliamos um ativo ou uma carteira com base em duas métricas principais:

Retorno esperado: a média dos retornos históricos, que representa o ganho potencial do ativo.
Risco: normalmente medido pelo desvio padrão dos retornos (volatilidade), que expressa a incerteza em torno do retorno esperado.

A escolha racional de investimentos

Dado um conjunto de ativos, um investidor racional seguirá duas regras simples:

Para um mesmo nível de risco, ele escolherá o ativo com maior retorno esperado.
Para um mesmo retorno esperado, ele optará pelo ativo com menor risco.

Essa lógica nos leva ao chamado princípio da dominância:

Um ativo A domina o ativo B se A oferece o mesmo risco com maior retorno ou o mesmo retorno com menor risco.

Em outras palavras, se um ativo entrega mais retorno para o mesmo risco (ou menos risco para o mesmo retorno), ele é a melhor escolha.

O trade-off entre risco e retorno

Nem sempre conseguimos ativos com baixo risco e alto retorno. Por isso, é comum que o investidor precise fazer compromissos: aceitar mais risco para buscar retornos maiores.

Esse é o trade-off clássico entre risco e retorno. Em termos gráficos, esse conceito é frequentemente representado pela fronteira eficiente de Markowitz, que mostra as carteiras que otimizam o retorno para cada nível de risco.

Visualizando a relação risco-retorno no Python

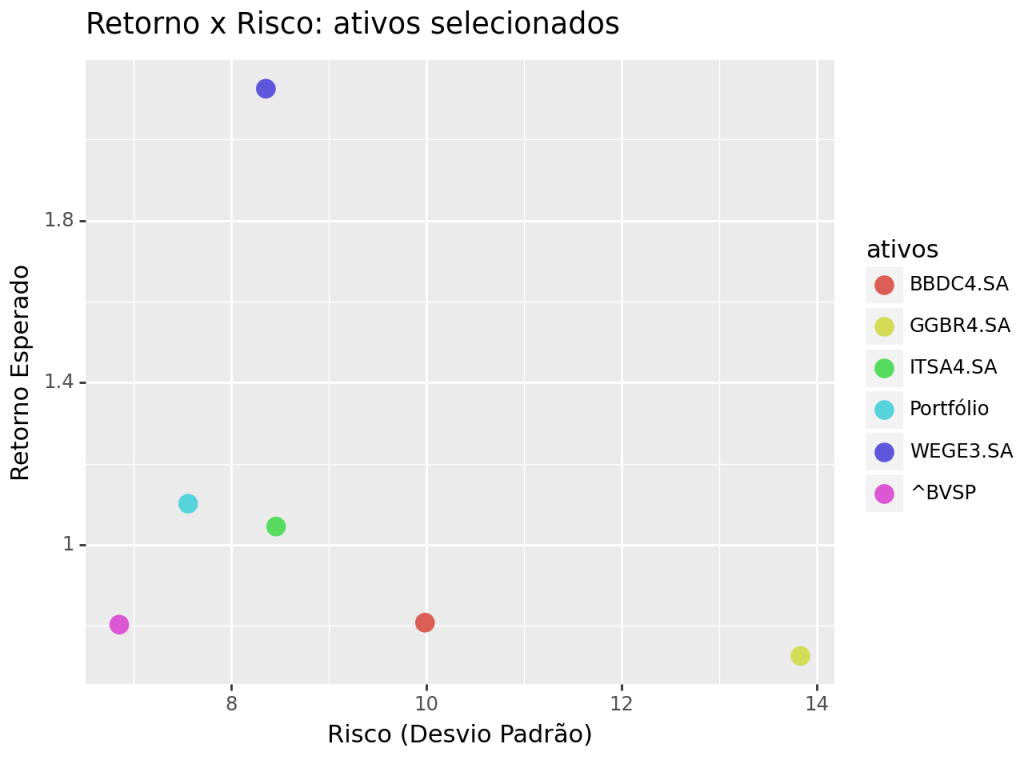
Para ilustrar esse conceito na prática, criamos um gráfico de dispersão com os ativos analisados e uma carteira hipotética, utilizando a biblioteca plotnine (inspirada no ggplot2 do R).

Nesse gráfico, cada ponto representa um ativo (ou a carteira), posicionado de acordo com:

O risco (desvio padrão dos retornos) no eixo x;
O retorno esperado (média dos retornos) no eixo y.

Exemplo Prático: Como a Diversificação Melhora a Relação de Risco-Retorno

Para ilustrar os conceitos apresentados, construímos um portfólio com pesos iguais entre os ativos e analisamos sua posição em um gráfico de dispersão que relaciona o retorno esperado ao risco (desvio-padrão).

A ideia central aqui é visualizar como a diversificação afeta essa relação de risco-retorno. Ao combinar ativos com comportamentos distintos — especialmente com baixa correlação — conseguimos formar uma carteira que apresenta menor risco para um mesmo nível de retorno, ou, alternativamente, maior retorno para um mesmo nível de risco. Este é o benefício fundamental da diversificação, inclusive quando consideramos um índice como o Ibovespa.

Para entender melhor esse comportamento, podemos criar diferentes portfólios a partir dos mesmos ativos, mas variando os pesos atribuídos a cada um deles. Assim, simulamos várias combinações possíveis de alocação e, para cada uma, calculamos o risco e o retorno resultantes.

Ao plotar essas combinações, observamos que os portfólios mais eficientes — ou seja, aqueles que representam a melhor troca entre risco e retorno — ficam posicionados à esquerda do gráfico, indicando menor risco para determinado retorno. Essas carteiras são preferíveis segundo o princípio da dominância, pois não são superadas por nenhuma outra em ambos os critérios.

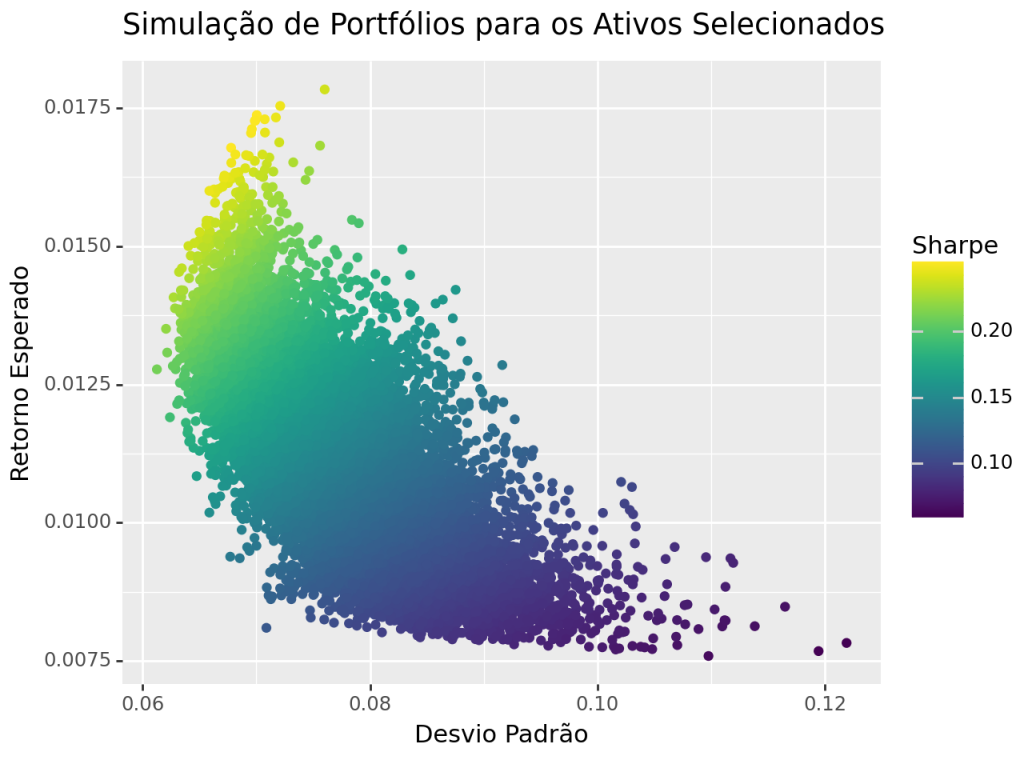
É justamente nesta região que encontramos portfólios com maior Índice de Sharpe — uma métrica amplamente utilizada em finanças que expressa o retorno em excesso por unidade de risco. Em outras palavras, essas combinações de ativos oferecem o melhor desempenho ajustado ao risco, sendo resultado direto da baixa correlação entre os ativos que as compõem.

Esse exercício nos permite compreender na prática como uma análise criteriosa da relação risco-retorno, aliada à diversificação e ao uso de métricas adequadas, pode guiar decisões mais racionais na construção de portfólios.

Quer aprender mais?

Conheça nossa Formação do Zero à Análise de Dados Econômicos e Financeiros usando Python e Inteligência Artificial. Aprenda do ZERO a coletar, tratar, construir modelos e apresentar dados econômicos e financeiros com o uso de Python e IA.

Referências

ELTON, Edwin J.; GRUBER, Martin J.; BROWN, Stephen J.; GOETZMANN, William N.
Modern portfolio theory and investment analysis. 9. ed. Hoboken: Wiley, 2014.

TSAY, Ruey S.
Analysis of financial time series. 3. ed. Hoboken: Wiley-Interscience, 2010.

Compartilhe esse artigo

Comente o que achou desse artigo

Boletim AM

Encontre o seu conteúdo

Categorias

Artigos mais acessados

Como avaliar a relação de risco-retorno de ações no Python

O que são LLMs?

O que são Agentes de IA?

As diferentes formas de avaliar o erro de um modelo de previsão

Previsão do CPI usando text mining

Nowcasting do PIB usando a linguagem R

Outros artigos relacionados

Como avaliar a relação de risco-retorno de ações no Python

Neste tutorial apresentamos o conceito de risco-retorno para a avaliação de ações, tomando como ferramenta de análise a linguagem Python.

O que são LLMs?

Anteriormente, aprendemos que cada Agente precisa de um Modelo de IA em seu núcleo, e que os LLMs são o tipo mais comum de modelos de IA para esse propósito.

Agora, vamos aprender o que são LLMs e como eles impulsionam os Agentes. Esta seção oferece uma explicação técnica concisa sobre o uso de LLMs.

O que são Agentes de IA?

O que é um agente e como ele funciona? Como agentes tomam decisões usando racioncínio e planejamento? Neste artigo, nosso objetivo é investigar estas questões para construir um conhecimento fundamental sobre AI agents.

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!

Boletim AM

Receba diretamente em seu e-mail gratuitamente nossas promoções especiais e conteúdos exclusivos sobre Análise de Dados!