O Value At Risk é uma importante medida de risco no mundo das finanças, que estima a probabilidade de perda monetária em um dado horizonte de tempo. Se tornou famosa por sua simplicidade e pelo fato de estimar as perdas ao longo do tempo dado um nível de confiança. Existem diversas formas de se calcular o VaR, e no post de hoje mostraremos duas formas, a forma gaussiana (normal) e a histórica.
Há diversos métodos para se calcular o VaR, dentre aqueles relativamente mais simples, que podem ser o ponto inicial para aqueles que estão iniciando os estudos e a prática com medidas de risco, até aqueles que possuem uma maior nível de complexidade. Como diversas outras medidas de risco, o cálculo do VaR deve ser feito a partir dos retornos dos ativos, mais comumente os retornos contínuos, por conta de suas medidas estatísticas.
Historical Value at Risk
A primeira forma de calcular o VaR que elencaremos aqui pode ser através do Historical VaR, que calcula a perda monetária com base em um nível de probabilidade dado um quantil do retornos negativos passados. Esse método é útil quando se obtém um nível grande de dados passados, ou seja, por definição é uma analise ex-post da distribuição de retorno.
Em que é o quantil empírico dos retornos negativos da série.
Gaussian Value At Risk
Outra forma de calcular o VaR é assumindo que os seus retornos são normais, isto é, possui um distribuição Gaussiana
. Deste modo, é necessário estimação da média dos retornos, a variância (e consequentemente o desvio padrão) e os retornos passados da série.
onde é o quantil da distribuição normal
Outros métodos de estimação de VaR levam em consideração as características das séries de retornos, bem como outro meios estimação para a volatilidade e a média.
library(quantmod) library(PerformanceAnalytics) library(magrittr) library(timetk) library(ggplot2)
Para calcular o VaR devemos ter em mãos os retornos passados dos ativos.
# Retiramos os preços
tickers <- c("PETR4.SA", "VALE3.SA", "LAME3.SA")
env <- new.env()
getSymbols(tickers,
auto.assign = TRUE,
warnings = FALSE,
src = "yahoo",
env = env)
prices_list <- lapply(env, Ad)
prices <- do.call(merge, prices_list)
# Transformamos em log retornos returns <- Return.calculate(prices, method = "log") %>% na.omit() %>% `colnames<-`(tickers)
Com os retornos diários em mãos, podemos utilizar o pacote {PerformanceAnalytics} para auxiliar no cálculo do VaR. A função VaR possibilita calcular a medida em diferentes métodos (no qual utilizaremos somente o historical e gaussian) e também a um dado nível de confiança. É possível também adicionar diferentes parâmetros na função, o que deixaremos para outro momento.
# utilizamos o Portfolio Analytics para calcular o VaR ## Historical var_historical <- VaR(R = returns, p = 0.99, method = "historical") var_historical
## Gaussian var_gaussian <- VaR(R = returns, p = 0.95, method = "gaussian") var_gaussian
É possível também juntar os retornos das ações em torno de um portfólio dentro da função, possibilitando conferir a contribuição de cada ativo para o risco. Para isso, definimos de forma aleatórias os pesos de cada ação e inserimos nos argumentos da função.
# Definimos os pesos do portfólio w <- c(0.65, 0.15, 0.20) # Calcula o VaR com o portfolio VaR(returns, p = 0.99, weights = w, portfolio_method = "component")
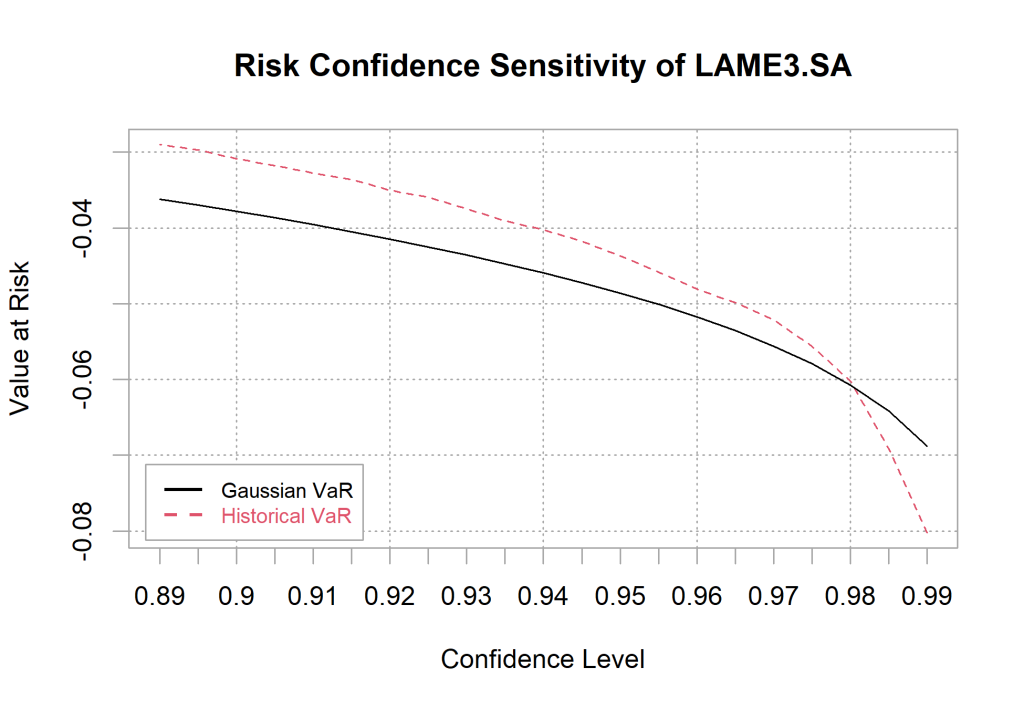
Uma forma interessante de averiguar os resultados dos diferentes métodos com diversos níveis de confiança, pode ser visto utilizando a função chart.VaRSensitivity.
chart.VaRSensitivity(R = returns$LAME3.SA,
methods = c("GaussianVaR",
"HistoricalVaR"))
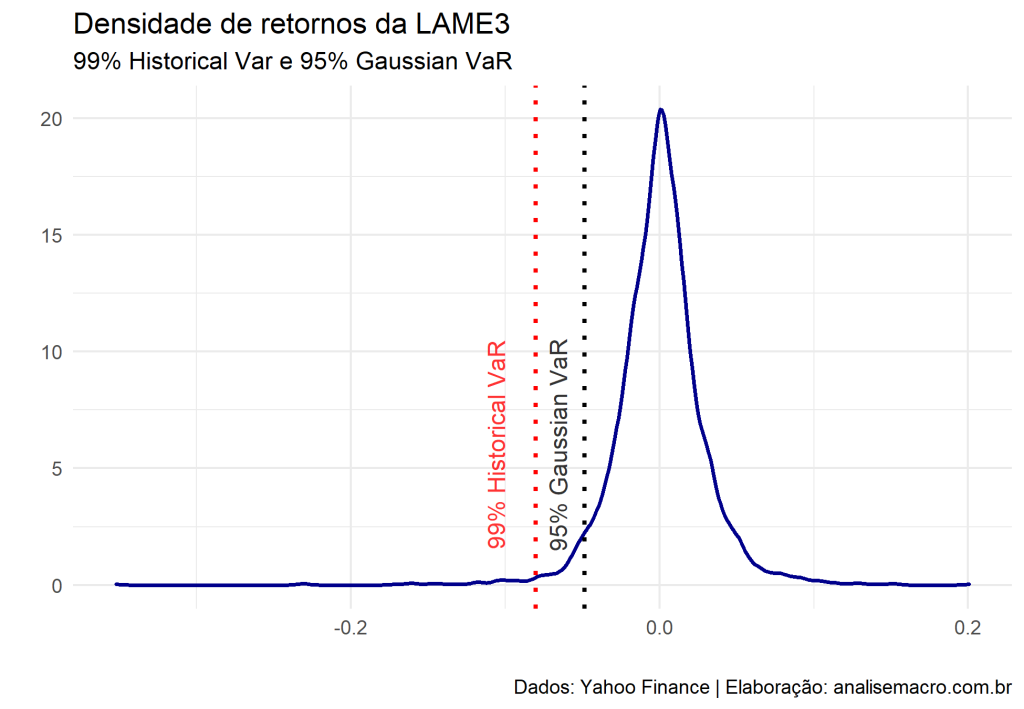
Por fim, vemos através de um gráfico de densidade dos retornos onde a possibilidade de perda.
returns_tbl <- tk_tbl(returns,
preserve_index = TRUE,
rename_index = "date")
ggplot(returns_tbl, aes(x = LAME3.SA))+
geom_density(color = "darkblue",
size = .8)+
geom_vline(xintercept = var_historical[,"LAME3.SA"],
linetype = "dotted",
color = "red",
size = 1)+
annotate(geom = "text",
x = var_historical[,"LAME3.SA"],
y = 6,
label = paste("99% Historical VaR"),
color = "red",
angle = 90,
alpha = .8,
vjust = -1.75)+
geom_vline(xintercept = var_gaussian[,"LAME3.SA"],
linetype = "dotted",
color = "black",
size = 1)+
annotate(geom = "text",
x = var_gaussian[,"LAME3.SA"],
y = 6,
label = paste("95% Gaussian VaR"),
color = "black",
angle = 90,
alpha = .8,
vjust = -1)+
theme_minimal()+
labs(title = "Densidade de retornos da LAME3",
subtitle = "99% Historical Var e 95% Gaussian VaR",
caption = "Dados: Yahoo Finance | Elaboração: analisemacro.com.br",
x = "",
y = "")
________________________
(*) Para conhecer mais sobre medidas de risco do mundo das finanças, veja nossos de Cursos de Finanças Quantitativas.
________________________