Introdução
Uma importante medida em finanças é o risco associado a um ativo e a volatilidade de ativos é talvez a medida de risco mais utilizada. Há, entretanto, diversas medidas de volatilidade. Portanto, no post de hoje, iremos verificar as características da volatilidade, os principais modelos e a possibilidade de estimação usando o R e o Python.
O objetivo aqui será o de entender as características da volatilidade de ativos, bem como estudar modelos que possam ser aplicados para explicá-la.
Para obter todo o código do processo de criação dos gráficos abaixo, faça parte do Clube AM, o repositório de códigos da Análise Macro, contendo exercícios semanais.
Características da Volatilidade
Ainda que a volatilidade seja bem definida, ela não é diretamente observada na prática. Nós observamos os preços dos ativos e seus derivativos. A volatilidade deve ser, então, estimada com base nesses preços observados.
Ainda que a volatilidade não seja diretamente observada, ela apresenta algumas características comuns associadas aos retornos dos ativos. Listamos abaixo algumas delas:
- A volatilidade é alta em certos períodos e baixa em outros, configurando o que a literatura chama de ;
- A volatilidade evolui de maneira contínua, de modo que não são comuns;
- A volatilidade costuma variar em um intervalo fixo;
- A volatilidade costuma reagir de forma diferente a um aumento muito grande nos preços e a um decréscimo igualmente muito grande, com o último representando maior impacto.
Essas características implicam que, de modo geral, a volatilidade é uma série estacionária. Ademais, essas características determinam a forma como os modelos serão construídos.
De fato, alguns modelos de volatilidade são formatados justamente para corrigir a inabilidade dos atualmente existentes em capturar algumas das características mencionadas acima.
Na prática, estima-se a volatilidade de um ativo com base nos seus preços ou derivativos. Tipicamente, três tipos de volatilidade são consideradas:
- Volatilidade como o desvio-padrão condicional dos retornos diários, a base do que veremos nessa seção;
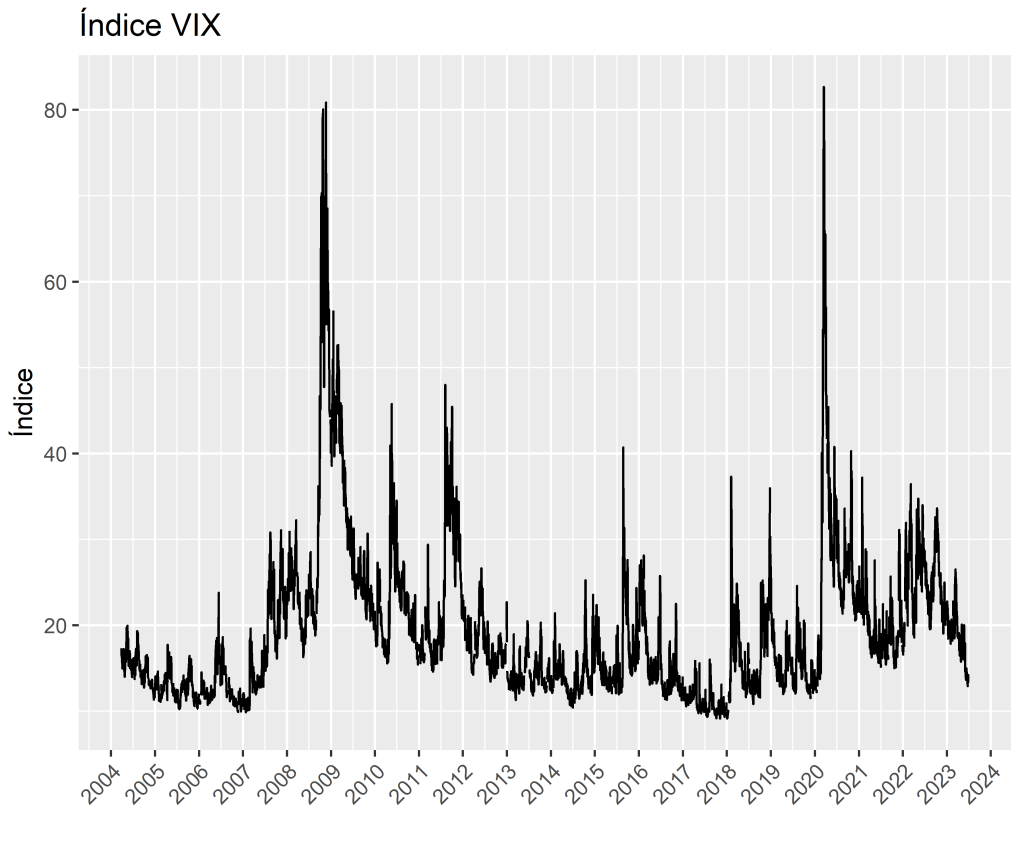
- Volatilidade implícita, obtida a partir de fórmulas de precificação (como Black-Scholes), com base nos preços do mercado de opções, é possível deduzir a volatilidade do preço da ação. Um exemplo, como visto acima, desse tipo de procedimento é o
VIX Index; - Volatilidade realizada, obtida com base em dados financeiros de alta frequência, como, por exemplo, retornos intraday de 5 minutos.
Estrutura do modelo
Tomemos como o log retorno de um ativo no tempo
. A ideia básica por trás do estudo de volatilidade é que a série
está serialmente não correlacionada ou com pequenas correlações em série de ordem menor, mas que é uma série dependente.
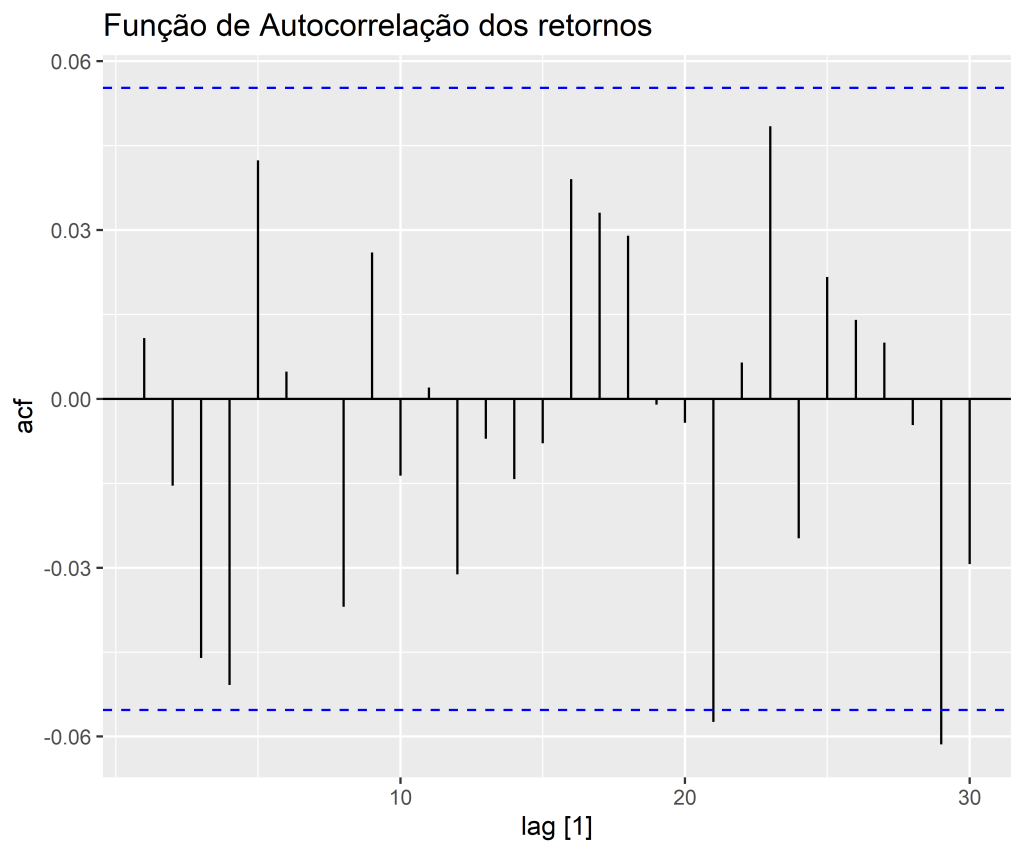
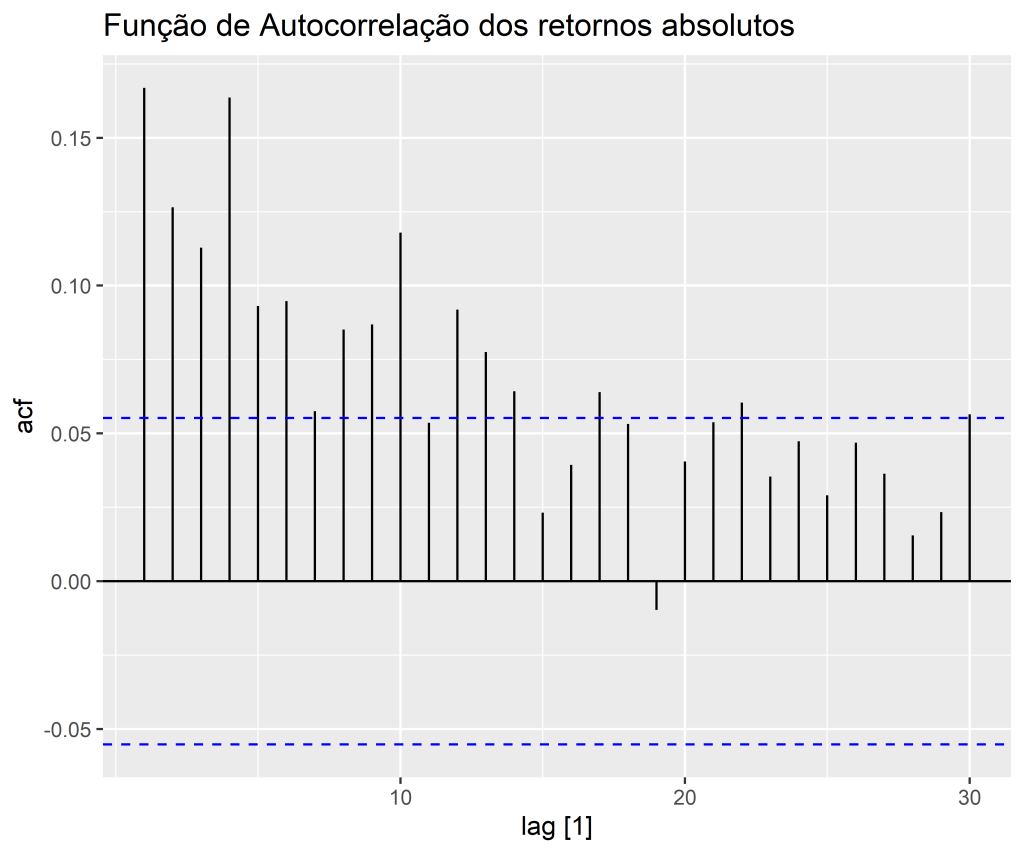
Para ilustrar, considere o log retorno do preço de fechamento das ações da Amazon no período de 2014 até 2018. É importante notar, através do gráfico de Autocorrelação, a diferença do retornos para os retornos absolutos.
Conquanto a série de log retorno aparenta ser estacionária, as funções de autocorrelação sugerem uma correlação serial não significativa quando considerada a série .
Já quando consideramos , a série se mostra serialmente correlacionada (é possível confirmar esse tipo de questão utilizando o teste *Ljung-Box*.
Consequentemente, os log retornos mensais se mostram serialmente não correlacionadas, porém dependentes. Essa é a característica que um modelo de volatilidade univariada é designado a capturar.
De modo a colocar os modelos de volatilidade em uma perspectiva apropriada, é informativo considerar a média e a variância condicionais de dado
, isto é,
onde é o conjunto de informação disponível no período
. Tipicamente,
consiste em todas as funções lineares dos retornos passados.
Modelos de heterocedasticidade condicional, a propósito, podem ser classificados em duas categorias gerais. Na primeira categoria estão aqueles que utilizam uma função determinística para descrever a evolução de , já na segunda estão aqueles que utilizam uma equação estocástica para tal.
De modo a construir nosso modelo de volatilidade, a equação para deveria ser simples, de modo que nós assumimos que
segue uma média zero, uma média constante ou um modelo de série temporal simples tal qual um modelo
.
Assim, dado que ,
será dado por
(1)
Se algumas variáveis explanatórias estiverem disponíveis, nós podemos aumentar o modelo , onde
{#eq-mu} onde denomina a série de retorno ajustada após remoção do efeito das variáveis explanatórias, e
são as variáveis explanatórias disponíveis no período
.
Por fim, será referido como um choque ou inovação do retorno de um ativo no período
. O modelo para
em @eq-mu é referido como equação da média para
e o modelo para
é a equação de volatilidade para
.
Assim, modelar heterocedasticidade condicional equivale a aumentar a equação dinâmica que determina a evolução ao longo do tempo da variância condicional do retorno do ativo a partir de um modelo de série temporal.
Construção do modelo
Construir um modelo de volatilidade para uma série de retorno de ativo consiste em quatro etapas:
- Especificar uma equação da média testando para dependência serial nos dados e, se necessário, construir um modelo econométrico para a série de retorno de modo a remover qualquer dependência linear;
- Utilizar os resíduos da equação da média para testar efeitos ARCH;
- Especificar um modelo de volatilidade se o efeito ARCH foi estatisticamente significativo e performar uma estimativa conjunta da equação da média e da volatilidade;
- Checar o modelo estimado com cuidado e refinar, caso necessário.
Especificando a equação da média
Para a maioria das séries de retorno de ativos, a correlação serial é fraca, se existente. Assim, construir uma equação da média equivale a remover a média amostral dos dados se a média amostral é significativamente diferente de zero. Para algumas séries de retorno diário, um AR simples pode ser suficiente.
Em alguns casos, porém, a equação da média pode precisar de algumas variáveis explanatórias tal qual uma variável indicativa de feriados ou efeitos sazonais. Em outros casos, ademais, a equação da média consiste apenas em uma constante.
Desvio padrão anualizado Móvel
Existem muitas formas de estimar a volatilidade de um ativo financeiro. Lembramos que retorno de um ativo financeiro pode ser considerado uma variável aleatória, que possui uma distribuição próxima da normal (gaussiana).
O desvio padrão, um dos parâmetros da distribuição gaussiana, como medida que representa o Risco/Volatilidade do ativo financeiro, devido a sua capacidade de mensurar o desvio em relação ao retorno do ativo.
Um alto valor do desvio padrão, significa que a distribuição é ampla e que o preço do ativo pode subir e cair muito, por outro lado, valores pequenos dos desvios representam que a distribuição é estreita e que o preço do ativo não varia muito.
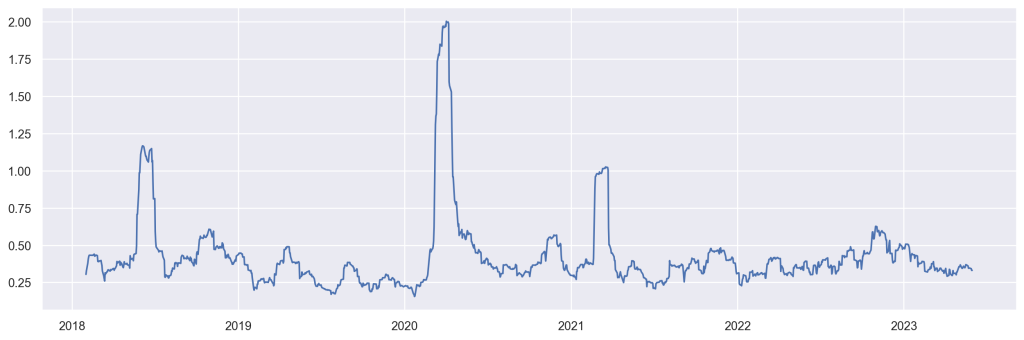
Vejamos uma forma interessante de mensurar a volatilidade por meio do desvio padrão anualizado em janelas de tempo de 1 mês em dias úteis (22 dias).
A equação do indicador construído abaixo é representado por
O gráfico abaixo representa o Desvio Padrão Anualizado em janelas móveis de 22 dias dos retornos simples da ação PETR4. Veja o comportamento da série, é possível notar os períodos de baixa e alta volatilidade.
ARCH
O primeiro modelo que proveu um framework sistemático para a volatilidade é o ARCH, acrônimo para Autoregressive Conditional Heteroskedasticity.
A ideia básica desse tipo de modelo é que (i) o choque de um retorno de ativo é serialmente não correlacionado, mas dependente; e (ii) a dependência de
pode ser descrita por uma função quadrática dos seus valores defasados, isto é,
{#eq-arch}
onde é uma sequência de variáveis aleatórias independentes e idênticamente distribuídas com média zero e variância igual 1,
e
para
(os coeficientes
devem satisfazer algumas condições de regularidade de modo a garantir que a variância incondicional de
seja finita).
Modelos do tipo ARCH oferecem algumas vantagens para se analisar retornos de ativos, dentre as quais se destacam: (i) o modelo pode produzir volatility clusters; (ii) os choques do modelo possuem caudas densas. A despeito disso, é preciso considerar algumas restrições desse tipo de modelo, a saber:
- O modelo assume que choques negativos e positivos possuem o mesmo efeito sobre a volatilidade;
- O modelo ARCH é bastante restritivo, o que limita sua habilidade em capturar excessos de curtose;
- O modelo ARCH não provê nenhum novo para entender a fonte das variações em séries temporais financeiras. Ele apenas provê uma forma mecânica de descrever o comportamento da variância condicional;
- Modelos ARCH são predispostos a superestimar a volatilidade porque eles respondem devagar a choques grandes, porém isolados, sobre séries de retorno.
Abaixo, podemos verificar os resultados estatísticos de um ARCH estimado via a biblioteca arch do Python. Os mesmos resultados podem ser obtidos no R por meio do pacote rugarch.
Código
Código
Zero Mean - ARCH Model Results
==============================================================================
Dep. Variable: Adj Close R-squared: 0.000
Mean Model: Zero Mean Adj. R-squared: 0.001
Vol Model: ARCH Log-Likelihood: 2876.45
Distribution: Normal AIC: -5748.91
Method: Maximum Likelihood BIC: -5738.54
No. Observations: 1320
Date: Mon, Jul 03 2023 Df Residuals: 1320
Time: 13:48:50 Df Model: 0
Volatility Model
============================================================================
coef std err t P>|t| 95.0% Conf. Int.
----------------------------------------------------------------------------
omega 5.6969e-04 5.056e-05 11.266 1.922e-29 [4.706e-04,6.688e-04]
alpha[1] 0.3451 0.103 3.350 8.074e-04 [ 0.143, 0.547]
============================================================================
Covariance estimator: robustCódigo
omega 0.000570
alpha[1] 0.345102
Name: params, dtype: float64GARCH
Apesar do modelo ARCH ser simples, ele geralmente requer muitos parâmetros de modo a descrever adequadamente a volatilidade dos retornos dos ativos. De modo a manter o modelo simples, algumas alternativas podem ser pensadas. Uma delas é considerar para uma série de log retorno , sendo
um choque no período
, de modo que
segue um modelo ARCH generalizado, isto é, um GARCH(m,s), tal que
{#eq-garch}
onde é também uma sequência de variáveis aleatórias iid com média zero e variância igual a 1,
,
,
e
.
De modo a entender as propriedades do modelo GARCH, convém fazer algumas modificações em @eq-garch. Tomemos , assim
.
Iterando para
na equação @eq-garch, nós podemos reescrever o modelo GARCH como
{#eq-garch2} Assim, o modelo GARCH pode ser considerado uma aplicação da ideia dos modelos ARMA ao quadrado de .
Abaixo, podemos verificar os resultados estatísticos de um ARCH estimado via a biblioteca arch do Python. Os mesmos resultados podem ser obtidos no R por meio do pacote rugarch.
Código
Zero Mean - GARCH Model Results
==============================================================================
Dep. Variable: Adj Close R-squared: 0.000
Mean Model: Zero Mean Adj. R-squared: 0.001
Vol Model: GARCH Log-Likelihood: 2947.35
Distribution: Normal AIC: -5888.70
Method: Maximum Likelihood BIC: -5873.14
No. Observations: 1320
Date: Mon, Jul 03 2023 Df Residuals: 1320
Time: 13:48:51 Df Model: 0
Volatility Model
============================================================================
coef std err t P>|t| 95.0% Conf. Int.
----------------------------------------------------------------------------
omega 9.5348e-05 3.828e-05 2.491 1.274e-02 [2.032e-05,1.704e-04]
alpha[1] 0.2000 9.642e-02 2.074 3.805e-02 [1.103e-02, 0.389]
beta[1] 0.7000 0.102 6.871 6.388e-12 [ 0.500, 0.900]
============================================================================
Covariance estimator: robust
Código
omega 0.000095
alpha[1] 0.200000
beta[1] 0.700000
Name: params, dtype: float64_____________________
Quer saber mais?
Veja nossa trilha de cursos de Finanças Quantitativas

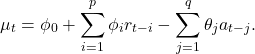
![Rendered by QuickLaTeX.com \[\mu_t = \phi_0 + \sum_{i=1}^{k} \beta_i x_{i,t-1} + \sum_{i=1}^{p} \phi_i y_{t-i} - \sum_{j=1}^{q} \theta_j a_{t-j},\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-f58750196201d63b40cc90a520375692_l3.png)
![Rendered by QuickLaTeX.com \[\sigma^2 =\frac{1}{M-1} \sum_{i=1}^M E[(R_t - E(R_t)^2] \times \sqrt{252}\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-45f14d5494d26874a99e21e686c995c1_l3.png)
![Rendered by QuickLaTeX.com \[a_t = \sigma^t \varepsilon_t, \quad \sigma_t^2 = \alpha_0 + \sum_{i=1}^{m} \alpha_i a_{t-i}^2 + \sum_{j=1}^{s} \beta_j \sigma_{t-j}^2,\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-3edbb9edc95910c734772e9e475c65a4_l3.png)
![Rendered by QuickLaTeX.com \[a_t^2 = \alpha_0 + \sum_{i=1}^{max(m,s)} (\alpha_i + \beta_i) a_{t-i}^2 + \eta_t + \sum_{j=1}^{s} \beta_j \eta_{t-j}\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-b53c0087704f84ff532179bf637a9054_l3.png)

