A volatilidade implícita é uma medida que captura a expectativas dos investidores em relação à variação futura dos preços de um ativo subjacente (opções), como ações, moedas, commodities, entre outros. Veremos como é possível estimar a volatilidade implícita de ações utilizando o R e o Python como ferramentas.
Quando um investidor compra ou vende opções, ele está apostando na direção futura dos preços do ativo subjacente. A volatilidade implícita reflete as percepções do mercado sobre a probabilidade de grandes movimentos de preço no futuro. Se os investidores acreditam que os preços do ativo terão grandes flutuações, a volatilidade implícita será alta. Por outro lado, se eles acreditam que os preços terão pouca variação, a volatilidade implícita será baixa.
A volatilidade implícita é um valor calculado a partir dos preços das opções negociadas no mercado. Ela pode variar com base em fatores como eventos econômicos, anúncios corporativos, mudanças nas taxas de juros e outros elementos que possam afetar a percepção dos investidores sobre os riscos futuros.
Os traders e investidores utilizam a volatilidade implícita para avaliar o valor relativo das opções. Opções com volatilidade implícita alta tendem a ser mais caras, porque existe uma maior expectativa de grandes movimentos de preço. Opções com volatilidade implícita baixa são geralmente mais baratas, pois há uma menor expectativa de variação significativa nos preços do ativo subjacente.
É derivada dos preços das opções negociadas no mercado. Não é uma medida direta, mas sim um valor calculado a partir dos preços das opções e de um modelo de precificação, como o Modelo Black-Scholes ou outros modelos de volatilidade estocástica mais avançados.
Para obter a volatilidade implícita, geralmente segue-se este processo:
1. Coleta de dados: É necessário obter os preços de mercado das opções para um determinado ativo subjacente em diferentes preços de exercício e datas de vencimento. Você precisará dos preços de compra (bid) e venda (ask) para várias opções.
2. Escolha de um modelo de precificação: O Modelo Black-Scholes é um dos modelos mais amplamente utilizados para precificar opções e calcular a volatilidade implícita. Para usar o Black-Scholes, você precisará determinar a taxa de juros livre de risco, o preço atual do ativo subjacente, o preço de exercício da opção, o tempo até o vencimento e os preços das opções.
3. Cálculo da Volatilidade Implícita: Depois de encontrar a volatilidade que faz com que os preços calculados pelo modelo correspondam aos preços de mercado, essa volatilidade é considerada a volatilidade implícita para essas opções específicas.
O que é o Modelo Black-Scholes?
O modelo Black-Scholes é um modelo matemático utilizado para precificar opções financeiras e calcular a volatilidade implícita. Ele foi desenvolvido por Fischer Black, Myron Scholes e Robert Merton na década de 1970 e é amplamente usado no mercado financeiro para avaliar opções de compra (call) e opções de venda (put).
O modelo Black-Scholes é baseado em várias premissas simplificadoras:
1. Mercado Eficiente: O modelo assume que os mercados são eficientes e que não há oportunidades de arbitragem. Isso significa que não há maneira de obter lucro sem risco.
2. Sem Custos de Transação: O modelo não considera custos de transação ao comprar ou vender opções.
3. Sem Dividendos: Inicialmente, o modelo não considera o pagamento de dividendos pelo ativo subjacente durante a vida da opção.
4. Movimento Logarítmico dos Preços: O modelo assume que os preços dos ativos seguem um movimento logarítmico Browniano, o que implica que os retornos são normalmente distribuídos.
5. Volatilidade Constante: O modelo pressupõe que a volatilidade do ativo subjacente é constante ao longo do tempo.
6. Opções são do tipo europeias: apenas exercidas em sua expiração.
O cálculo do preço de uma opção usando o modelo Black-Scholes envolve as seguintes fórmulas:
Para uma opção de compra (call):
![\[C(s,t) = N(d_1) \cdot S - N(d_2) \cdot K \cdot e^{-rT}\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-591133ce0a2e4dc38e7844f7f1070246_l3.png "Rendered by QuickLaTeX.com")
Para uma opção de venda (put):
![\[P(s,t) = K \cdot e^{-rT} \cdot N(-d_2) - S \cdot N(-d_1)\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-e29254e480c565927622db8e25bcfdf6_l3.png "Rendered by QuickLaTeX.com")
Onde: - 
e 
são os preços da opção de compra e opção de venda, respectivamente. - 
é o preço do ativo subjacente. - 
é o preço de exercício da opção. - 
é a taxa de juros livre de risco constante. - 
é o tempo até o vencimento da opção. - 
é a função de distribuição acumulada da distribuição normal. - 
e 
são parâmetros calculados.
Antes de entendermos como calcular e , vamos compreender a intuição da fórmula.
A análise começa com o conceito de "valor intrínseco". Esse valor intrínseco é a parte do preço de uma opção que surge da diferença entre o preço atual da ação (ou outro ativo subjacente) e o preço de exercício da opção.
Para opções de compra (call options), o valor intrínseco é calculado como a diferença entre o preço atual da ação e o preço de exercício:
![\[\text{Valor Intrínseco} = \text{Preço da Ação} - \text{Preço de Exercício}\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-9984db281a2726cc33725f92eac00f71_l3.png "Rendered by QuickLaTeX.com")
Na notação da fórmula de Black-Scholes, isso seria:
![\[\text{Valor Intrínseco} = S - K\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-b7c51e99ac98ba6ffc2b7b7a08ac4580_l3.png "Rendered by QuickLaTeX.com")
Aqui, representa o preço da ação e é o preço de exercício. Isso é válido especialmente quando você olha para o momento da expiração da opção, quando o tempo restante para a opção expirar é zero. Nesse momento, o preço da opção é composto inteiramente pelo seu valor intrínseco, e qualquer valor adicional é considerado "valor extrínseco".
Porém, se você olhar apenas para o valor intrínseco, você acabaria ignorando opções que estão "Fora do Dinheiro" (OTM), ou seja, opções em que o preço de exercício está acima do preço da ação. Essas opções OTM têm valor mesmo que não tenham valor intrínseco, o que nos leva ao conceito de "valor extrínseco".
O valor extrínseco é a parte do preço da opção que não está diretamente relacionada à diferença entre o preço da ação e o preço de exercício. Ele leva em consideração fatores como o tempo até a expiração da opção e a volatilidade do ativo subjacente. Por exemplo, uma opção que tem mais tempo até o vencimento o seu preço pode se mover mais, e por isso deve ser avaliada mais alta do que uma opção com menos tempo restante.
O preço total de uma opção é, portanto, uma soma do seu valor intrínseco e extrínseco:
![\[\text{Preço da Opção} = \text{Valor Intrínseco} + \text{Valor Extrínseco}\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-407d661c9eb5d59dc7f703a597231ade_l3.png "Rendered by QuickLaTeX.com")
Ou, em termos de uma opção de compra:
![\[\text{Preço da Opção de Compra} = (S - K)⋅X = X⋅S - X⋅K\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-d3e9a8bb1e9ff955281d3392cca69564_l3.png "Rendered by QuickLaTeX.com")
Aqui, 
é o valor intrínseco e "X" é uma maneira de representar o valor extrínseco. Essa estrutura se assemelha à fórmula de Black-Scholes, que é uma ferramenta fundamental para precificar opções e outros derivativos financeiros.
O processo que acabamos de explorar é uma versão simplificada da derivação da fórmula de Black-Scholes. No entanto, ele fornece uma base sólida para entender como o preço de uma opção é formado e como o valor intrínseco e extrínseco se relacionam.
Agora que você sabe, é muito fácil encontrar o valor intrínseco de uma opção. Mas o que exatamente compõe o valor extrínseco de uma opção?
Para responder a essa pergunta, vamos dar uma olhada nos multiplicadores de S (Preço da Ação) e K (Preço de Exercício). K, o preço de exercício, é multiplicado por 
e por 
. A primeira multiplicação 
basicamente desconta o preço de exercício para o momento atual. Isso é feito comparando o preço de exercício com a taxa livre de risco e o tempo até o vencimento. A razão pela qual isso é feito é que o preço de uma opção deve ser afetado pela taxa livre de risco.
Por exemplo, se você pudesse obter o mesmo pagamento com um investimento completamente livre de risco como com uma opção arriscada, você nunca escolheria a opção. Portanto, o preço de uma opção reflete o retorno potencial que você poderia receber desde agora até o vencimento na taxa livre de risco.
Agora, vamos olhar para 
e , os outros dois multiplicadores restantes de e . 
é a função de distribuição acumulada que é usada para calcular probabilidades sob uma distribuição normal (uma curva de distribuição em forma de sino). Isso significa que gera um valor de probabilidade entre 0 e 100%.
Em termos simplificados, calcula a probabilidade estimada de que a opção será exercida. Isso só faz sentido quando a opção está "Dentro do Dinheiro" (ITM) ou, em outras palavras, quando (preço da ação) é maior do que (preço de exercício). Portanto, você também poderia dizer que é uma estimativa ajustada ao risco da probabilidade de que o preço futuro da ação fique acima do preço de exercício na expiração.
![\[d_1 = \frac{{\ln\left(\frac{S}{K}\right) + \left(r + \frac{{\sigma^2}}{2}\right)T}}{{\sigma \sqrt{T}}}\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-af44d1cb579f9cd5cc05197963c03707_l3.png "Rendered by QuickLaTeX.com")
![\[d_2 = d_1 - \sigma \sqrt{T}\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-d218c4aa6d39177bdf8acb95b1f35f95_l3.png "Rendered by QuickLaTeX.com")
O parâmetro 
representa a volatilidade implícita. O processo envolve calcular e , e então usar esses valores nas fórmulas para calcular os preços das opções.
Fatores que entram nessa probabilidade incluem:
- Tempo até a expiração: quanto mais tempo resta, maiores são as chances de o preço subjacente ultrapassar o preço de exercício;
- Volatilidade. Ações mais voláteis se movem muito mais e, consequentemente, têm maiores chances de ultrapassar o preço de exercício antes do vencimento (Preço da ação, preço de exercício, taxa livre de risco)
É mais difícil interpretar diretamente N(d1); no entanto, você pode tentar pensar nele como a probabilidade ajustada ao risco de que a opção não será exercida. Como é visível na fórmula para d1, N(d1) é sempre maior que N(d2), independentemente dos valores das variáveis. Isso faz sentido, pois o valor de uma opção nunca deve ser negativo. N(d1) também pode ser considerado o Delta grego da opção de compra (a sensibilidade da opção às mudanças no preço da ação), mas falaremos mais sobre isso posteriormente.
Volatilidade Implícita e a Fórmula de Black-Scholes na Prática
Agora vamos falar sobre o papel da volatilidade na fórmula de Black-Scholes. Em primeiro lugar, por que a volatilidade deveria afetar o preço de uma opção?
Imagine duas ações, XYZ e ABC, ambas a $100 e idênticas em todos os aspectos, exceto por sua volatilidade. XYZ é cerca de duas vezes mais volátil do que ABC. Agora, você precisa escolher entre comprar uma opção de compra com preço de exercício de $110 em XYZ ou ABC (mesmo preço). A escolha lógica seria a opção de XYZ, porque XYZ é mais volátil e, portanto, mais provável de subir e ultrapassar $110 do que ABC.
Em conclusão, ações mais voláteis devem ter opções com preços mais altos, porque oferecem mais oportunidades de lucro.
Dito isso, não deve ser apenas a volatilidade passada que determina o valor de volatilidade de uma opção. Em vez disso, deve ser a volatilidade entre o momento atual e a data de expiração da opção. Portanto, a fórmula de Black-Scholes usa o desvio padrão anualizado do retorno da ação como medida de volatilidade (σ). Isso também é chamado de volatilidade implícita.
O único problema é que a volatilidade implícita é o único input da fórmula de Black-Scholes que não é diretamente observável. Isso ocorre porque não conhecemos a distribuição dos retornos futuros de uma ação.
Mas se não conhecemos um dos inputs da fórmula de Black-Scholes, como podemos usá-la para calcular o preço de uma opção?
A resposta para essa pergunta é que não usamos. Na prática, a fórmula de Black-Scholes geralmente não é usada para calcular o preço de uma opção. Os preços das opções geralmente já são conhecidos e diretamente observáveis no mercado. Em vez disso, a fórmula de Black-Scholes é comumente usada para calcular a volatilidade implícita das opções.
Ao transformar a fórmula de Black-Scholes e inserir todos os valores observáveis (incluindo o preço da opção), podemos derivar a volatilidade implícita de uma opção. A volatilidade implícita derivada pode, por exemplo, ser usada para fazer estimativas da volatilidade futura de um ativo.
Além disso, o modelo de Black-Scholes é frequentemente usado para calcular preços teóricos de opções, inserindo uma volatilidade implícita teórica. Isso pode ser útil para simular e analisar possíveis negociações de opções.
Gregas
Vamos dar uma olhada em como os Gregos se relacionam com a fórmula de Black-Scholes. Como você pode ou não saber, as Gregas medem as mudanças no preço de uma opção para as mudanças em certos fatores de mercado. Em outras palavras, medem a sensibilidade do preço de uma opção às mudanças em determinados fatores de mercado.
Matematicamente falando, elas são derivadas parciais dos diferentes parâmetros da fórmula de Black-Scholes. Não vamos abordar a fórmula matemática de cada Grega neste artigo, ao invés disso, vamos explicar brevemente o que cada Grega mede:
- Delta: mede a sensibilidade do preço da opção às mudanças no preço do ativo subjacente. Um Delta de 0.3 significa que o preço da opção aumentaria em $0.3 para um aumento de $1 no preço do ativo subjacente. O Delta para opções de compra é N(d1) e N(d1) - 1 para opções de venda.
- Gama: mede a taxa de variação do Delta. Portanto, é a derivada parcial do Delta. Gama é calculado da mesma maneira para opções de compra e de venda.
- Theta: mede a sensibilidade de uma opção às mudanças no tempo até a expiração (decaimento do tempo). Isso significa que o Theta mostra quanto valor uma opção ganha ou perde com a passagem do tempo.
- Vega mede a sensibilidade de uma opção às mudanças na volatilidade implícita. Assim como para o Gama, a fórmula para o Vega é a mesma para opções de compra e de venda.
- Rho mede a sensibilidade de uma opção às mudanças na taxa livre de risco.
Embora as Gregas sejam calculados por meio das derivadas parciais dos diferentes parâmetros da fórmula de Black-Scholes, elas geralmente também são ajustados. Por exemplo, o Theta é ajustado para que seu valor represente a sensibilidade do preço da opção para a mudança de um dia em vez de um ano no tempo até a expiração.
As Gregas são amplamente usados no mundo do trading (de opções), pois são uma ótima ferramenta para medir o risco em relação a certos fatores de mercado. Isso lhe proporciona uma ótima base para gerenciar suas posições e exposição.
Volatility Smile
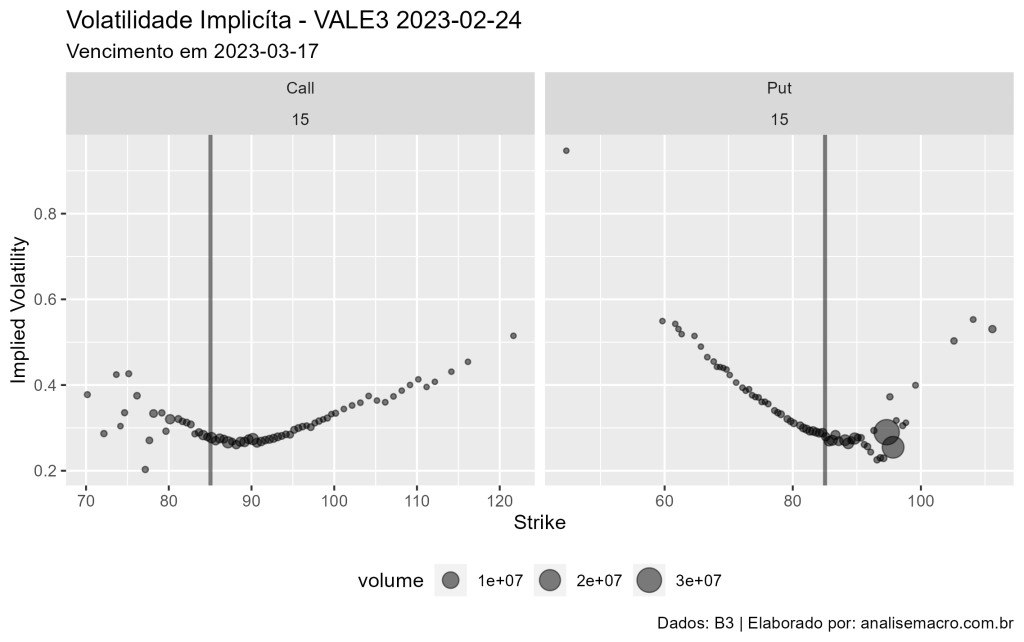
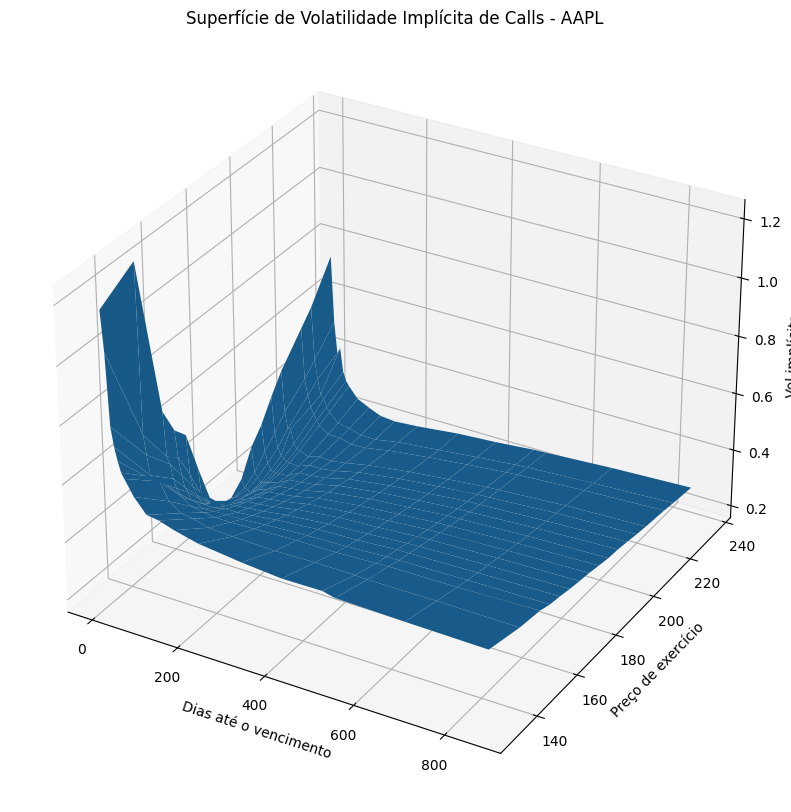
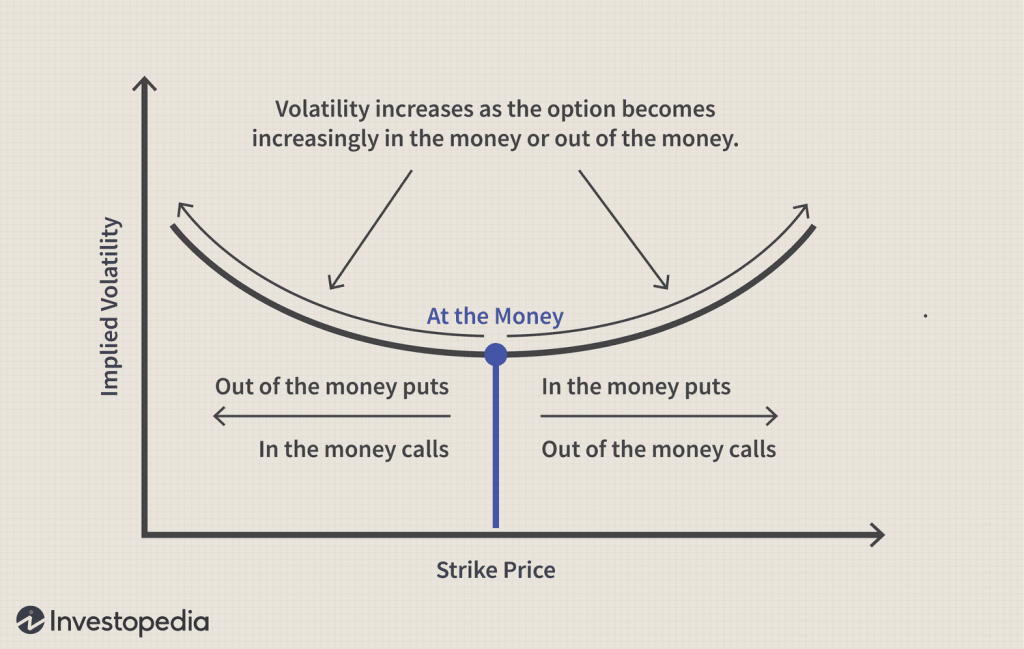
O "Volatility Smile" (sorriso da volatilidade) é um padrão gráfico observado nas curvas que representam a relação entre a volatilidade implícita e os preços de exercício das opções financeiras. Essa curva desvia-se da expectativa teórica da fórmula de Black-Scholes, que sugere que a volatilidade implícita deveria ser constante para todas as opções do mesmo ativo subjacente e expiração.
No entanto, na realidade, o Volatility Smile mostra que as opções fora do dinheiro (OTM) e as opções dentro do dinheiro (ITM) muitas vezes possuem volatilidades implícitas mais altas do que as opções no dinheiro (ATM) - aquelas em que o preço de exercício é mais próximo do preço atual do ativo subjacente. Isso cria um formato de "sorriso" na curva de volatilidade implícita em relação aos preços de exercício.
Existem algumas explicações possíveis para o Volatility Smile:
1. Caos dos Mercados: Os mercados financeiros podem ser turbulentos, levando a variações maiores nos preços das ações. Isso pode aumentar a demanda por opções fora do dinheiro como uma forma de proteção contra movimentos extremos.
2. Eventos Inesperados: Eventos imprevistos, como anúncios de resultados inesperados, crises políticas ou econômicas, podem causar movimentos bruscos nos preços das ações, levando a volatilidades implícitas mais altas.
3. Assimetria de Risco: Investidores podem estar dispostos a pagar prêmios extras por opções OTM, uma vez que a possibilidade de grandes movimentos de preço torna essas opções potencialmente lucrativas.
Em resumo, o Volatility Smile é uma observação da volatilidade implícita variando com base nos preços de exercício das opções. Ele sugere que os investidores atribuem diferentes níveis de incerteza a diferentes preços de exercício e expirações, levando a uma curva de volatilidade que se assemelha a um "sorriso". Isso é importante para os traders e investidores, pois pode influenciar as estratégias de negociação e a gestão de riscos ao lidar com opções.
Para obter todo o código em R e Python para os exemplos abaixo, faça parte do Clube AM, o repositório de códigos da Análise Macro, contendo exercícios semanais.
Estimando a Volatilidade Implícita no R
Podemos obter a Volatilidade Implicíta no R pode meio do processo de coleta de dados e estimação da volatilidade conforme a equação de Black-Scholes. Abaixo, verificar o "Volatility Smile" dos contratos da VALE3.
Estimando a Volatilidade Implícita no Python
Podemos obter a Volatilidade Implicíta no R pode meio do processo de coleta de dado. Abaixo, verificamos a superfícies de volatilidade dos contratos da AAPL.
_____________________
Quer saber mais?
Veja nossa trilha de cursos de Finanças Quantitativas
