Um dos maiores desafios é determinar se opções são baratas ou caras. Usualmente, realiza-se a transação tomando uma posição na volatilidade do ativo subjacente. Se o mercado espera uma alta na volatilidade, os preços das opções tendem a ser maiores. Se o mercado espera baixa volatilidade, a opção os preços tendem a serem baixos. Mostramos, conforme Burghard e Lane (1990) como se pode usar informações sobre a estrutura de maturidade das volatilidades históricas do ativo subjacente, representadas como cones de volatilidade, para determinar se as opções são baratas ou caras. Usamos a linguagem R como ferramenta para coleta e análise de dados.
Para saber como foi criado o exercício abaixo, faça parte do Clube AM, o repositório de códigos da Análise Macro, contendo exercícios semanais de R e Python.
O comprador de uma opção pode lucrar se qualquer uma das duas coisas acontecerem:
1. A volatilidade realizada do subjacente resulta ser maior do que a volatilidade implícita no preço pago pela opção;
2. O mercado revê em alta a sua percepção de quão volátil que acredita que o subjacente provavelmente será.
Da mesma forma, um vendedor de opções pode lucrar da volatilidade realizada que é inferior à volatilidade implícita ou de uma diminuição na percepção do mercado sobre a volatilidade.
Uma opção tem um horizonte de tempo específico - o seu tempo até à expiração - qualquer comparação da sua volatilidade implícita com uma volatilidade histórica de período fixo é inapropriado. O que precisamos é de uma ferramenta que permita comparar a previsão de volatilidade de uma opção com volatilidade histórica nos mesmos horizontes ou em horizontes semelhantes. Isto é, volatilidades implícitas das opções de quatro meses devem ser comparado com volatilidades históricas de quatro meses, enquanto as volatilidades implícitas das opções de um mês devem ser comparadas com as volatilidades históricas de um mês. Dito de outra forma, a única opção para a qual um a volatilidade histórica de trinta dias de negociação é um padrão apropriado é uma opção com trinta dias de negociação restante até o vencimento.
Volatility Cones
O objetivo do Cone de Volatilidade é ilustrar as faixas de volatilidade para diferentes negociações horizontes. Por exemplo, um período de um ano pode ser quebrado em períodos de um dia, uma semana e um mês. Isso nos daria cerca de 250 estimativas de volatilidade de um dia, cinquenta e duas estimativas de volatilidade de uma semana e doze estimativas de volatilidade de um mês.
A partir dos cones de volatilidade entendemos que as volatilidades históricas de curto prazo são muito mais variáveis do que as volatilidades de longo prazo.
Existem duas ideias básicas por trás do conceito dos cones de volatilidade. Primeiro, a volatilidade dos preços mostra uma tendência aparente chamada reversão à média, com base em qual poderia ser feita uma previsão sobre volatilidades em seus movimentos futuros. Os cones de volatilidade são construídos como referência para identificar se o valor implícito atual em relação as volatilidade realizadas são muito altas ou muito baixas.
Em segundo lugar, a correspondência do horizonte temporal é necessária enquanto aplicamos o método do cone de volatilidade na prática, ou seja, volatilidades implícitas de opções com 1 mês para vencimento são comparados com as volatilidades históricas de 1 mês, enquanto as volatilidades implícitas das opções com 3 meses até o vencimento são comparados com as volatilidades históricas de 3 meses.
Como construir os cones de volatilidade?
Primeiro, é necessário ter em mãos os preços do subjacente no mesmo período que a estimação da volatilidade implícita do ativo, de forma a comparar o período de tempo da volatilidade histórica com o tempo de expiração da opção. Com o preço de fechamento do ativo, calcula-se os log retornos e o desvio padrão anualizado. Isto é,
![\[R_i = ln(P_{t+1} / P_{t})\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-0804777edcb414fe57e7b572336ed595_l3.png "Rendered by QuickLaTeX.com")
![\[σ = \sqrt{\sum_{t}^{M}\frac{(R_{t} - \bar{R_{t}})^2}{M - 1}} * \sqrt{252}\]](https://analisemacro.com.br/wp-content/ql-cache/quicklatex.com-153b47ec93b7426156e1b0f5cf9994b8_l3.png "Rendered by QuickLaTeX.com")
Assim, σ é a volatilidade realizada ou histórica. Para construir os cones, calculamos janelas deslizantes de σ de tamanho M, escolhendo 15, 30, 45, 60 dias (ou que preferir). A partir das janelas, obtemos os valores mínimos, máximos, percentis 25 e 75 e a mediana de cada janela para construir os cones.
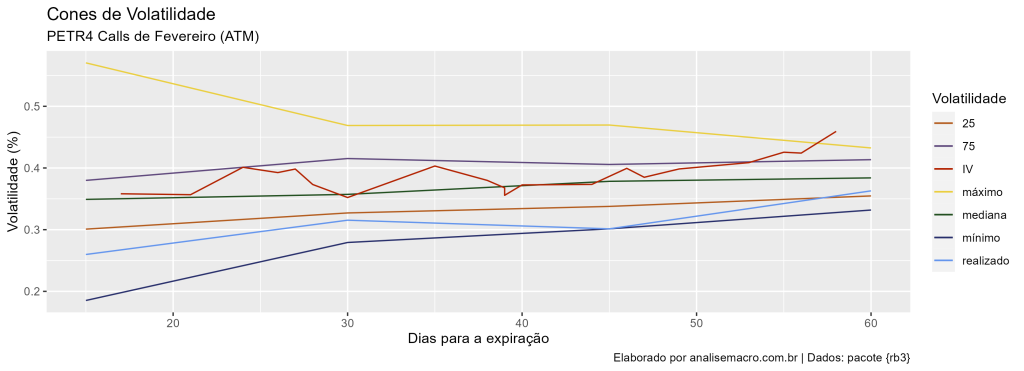
Para ilustrar considere um exemplo de opções ATM de fevereiro de 2023 da PETR4. Calculamos a volatilidade histórica e implícita, construindo as janelas de distribuição dos cones para volatilidade histórica. Realiza-se a leitura do eixo x da direita para a esquerda, isto é, maiores prazos de vencimentos iniciam no lado direito, e menores prazos ficam na posição à esquerda, enquanto a volatilidade histórica se inicia na esquerda.
_____________________
Quer saber mais?
Veja nossa trilha de cursos de Finanças Quantitativas
Referências
Burghardt, G., & Lane, M. (1990). How to tell if options are cheap. The Journal of Portfolio Management, 16(2), 72–78. doi:10.3905/jpm.1990.409259
